4. Логарифмическая функция

Как было показано в предыдущем пункте, множество всех корней уравнения представляется формулой

.

Значит, функция, обратная к , определена для любых и и задается формулой

.

Эта функция является многозначной, называется логарифмической и обозначается :

.

Значение логарифма , соответствующее , называется главным значением и обозначается :

.

Тогда . Следовательно, любое комплексное число имеет бесконечное множество логарифмов (значений логарифмической функции), из которых любые два отличаются на число кратное . Если , то . Но для этих существует еще бесконечно много значений логарифма. Например, .

Все логарифмы комплексного числа имеют одну и ту же действительную часть , а мнимые части отличаются на кратное . Следовательно, все логарифмы комплексного числа расположены на комплексной плоскости на одной прямой параллельной оси на расстоянии друг от друга.

Логарифмическая функция обладает следующими свойствами:

1. 

_{Доказательство.}

_{Действительно, преобразовывая левую часть равенства, получим:}

2. .

Доказательство.

Действуя так же, как в доказательстве свойства 1, получим:

.

Отметим, что эти равенства означают равенство множеств (в том смысле, что множества состоят из одних и тех же элементов).

Отсюда следует что, например, что . Приведем простой пример. Пусть . Тогда но . Следовательно, 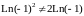, т.к. например но .

Чтобы выделить однозначные ветви функции , надо выделить области однолистности функции . Ими являются полосы шириной , параллельные действительной оси:

.

Функция однозначна на области , следовательно, на ней она имеет однозначначную обратную функцию многозначной функции . При отображении прямая переходит в луч , расположенный под углом к действительной оси. Если прямая проходит область от до , то луч сделает полный оборот вокруг начала координат. Следовательно, образом полосы является область – угол раствора , границей которого служит луч, расположенный под углом к действительной оси.

Обычно берут . Тогда, например, переводит плоскость с разрезом вдоль отрицательной части действительной оси в полосу .

Следовательно, в области получаем бесконечное множество различных однозначных ветвей функции . Каждая из ветвей характеризуется тем, что её значения принадлежат полосе .

Так как задает взаимно-однозначное отображение области на полосу и обратная функция имеет в производную для любых , то существует .

Точками разветвления логарифмической функции являются точки и . Т.к., описывая окружность вокруг начала координат сколько угодно раз в одном направлении, мы будем получать всё новые ветви: , то мы никогда не вернемся к исходной ветви . Поэтому точки и _{являются точками разветвления бесконечного порядка.}

5. Общие степенная и показательная функции

Введем понятие степени с произвольным показателем. Пусть – произвольное число. Если , то, как известно:

,

Если , где и – несократимая дробь, то:

,

где - единственное действительное положительное значение степени числа .

Пусть - иррациональное число. Зафиксируем и рассмотрим последовательность рациональных чисел, сходящуюся к . Тогда:

Это значение примем за одно из значений степени . Чтобы получить остальные значения, будем придавать различные значения. Так как два различных значения отличаются на , а это число не может быть целым кратным (так как – иррациональное число), то все значения , соответствующие различным значениям различны.

Итак, если , то

,

причем, если , то получаем одно значение, если , то значений, и если – иррациональное число, то бесконечное множество значений.

Пусть . Формулу можно записать в виде:

Определение 5.1. Пусть . Степенью комплексного числа называется .

Замечание. Для степени с произвольным показателем, вообще говоря, не выполняется правило сложения показателей при умножении степеней, а также правило умножения показателей при возведении степени в степень, т.е.:

1) , 2) .

Доказательство.

1. Действительно:

В то же время:

Из этого следует, что среди значений произведений содержатся все значения степени , но в общем случае имеются и другие значения. Для того чтобы имелось равенство , необходимо и достаточно, чтобы для любых целых 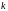и существовали такие целые и , что .

₂₎ Аналогично,

.

С другой стороны, . Значит, в общем случае .

Определение 5.2. Степенной функцией комплексной переменного называется функция вида .

Она определена для любых . Степенная функция в общем случае (но не всегда) многозначна. Если , то – конечнозначна ( -значна) и её точками разветвления порядка являются точки и , если , то – бесконечнозначна и её точками разветвления также являются точки и , но бесконечного порядка.

Каждому значению независимой переменной соответствует счетное множество значений степени . Если справа в определении брать одну определенную ветвь , то будем получать соответствующие ветви степенной функции. Например, .

Отдельные ветви, т.е. однозначные функции , являются аналитическими функциями на комплексной плоскости с разрезом вдоль отрицательной действительной полуоси. По правилу производной сложной функции:

.

Например, .

Определение 5.3. Функция вида , где и , называется общей показательной функцией.

Эта функция многозначна в силу многозначности и не имеет ни одной точки разветвления и её однозначные непрерывные ветви не могут непрерывно переходить одна в другую.

Чтобы получить определенную однозначную ветвь, надо фиксировать одно из значений .

Пусть , тогда:

, ,

.

При , т.е. когда берем главное значение , получим .

Зафиксируем у функции одно из значений логарифма: . Тогда мы получим однозначную ветвь функции и можем рассмотреть обратную к ней функцию. Получим:

.

Так как , то можно рассматривать как логарифм по основанию .

Определение 5.4. Логарифмом произвольного комплексного числа по некоторому основанию ( _– комплексное число) называется , где в знаменателе стоит одно фиксированное значение .

Например, пусть . Если фиксируем значение , равное 1, то получим:

.

Это и есть обычное определение натурального логарифма. Но можно взять . Тогда:

.

Это определение требует, таким образом, не только указания основания системы логарифмов, но и фиксации одного из значе­ний .