
- •«Многолистные и многозначные функции комплексного переменного»
- •§1. Функции комплексного переменного, дифференцируемость и аналитичность. Конформные отображения. 5
- •§2. Элементарные многозначные и многолистные функции 19
- •Глава II. Практическая часть 60
- •Введение
- •I. Теоретическая часть §1. Функции комплексного переменного, дифференцируемость и аналитичность. Конформные отображения.
- •1. Понятие функции комплексного переменного
- •2.Дифференцирование функции одной комплексной переменной
- •3. Геометрический смысл аргумента производной
- •4. Геометрический смысл модуля производной
- •5. Понятие о конформном отображении
- •§2. Элементарные многозначные и многолистные функции
- •Многочлен
- •Степенная функция и радикал
- •Показательная функция
- •Логарифмическая функция
- •5. Общие степенная и показательная функции
- •6. Тригонометрические функции
- •7. Гиперболические функции
- •8. Отображения, осуществляемые при помощи тригонометрических функций
- •9. Обратные тригонометрические функции
- •Глава II. Практическая часть
- •Заключение
- •Список литературы
§2. Элементарные многозначные и многолистные функции
Многочлен
Определение 1.1. Целой называется однозначная, аналитическая во всей конечной комплексной плоскости функция. Частным случаем является многочлен:
 .
.
Если
 ,
то
,
то
 .
Если
.
Если
 и
и
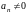 ,
то
,
то
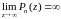 .
Пусть
.
Пусть
 -
произвольное число. Тогда уравнение
-
произвольное число. Тогда уравнение
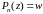 имеет
корней, среди которых могут быть равные
(кратные корни). Следовательно, у любой
точки
при отображении
имеет
корней, среди которых могут быть равные
(кратные корни). Следовательно, у любой
точки
при отображении
 существует
прообразов
существует
прообразов
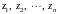 .
Прообразами точки
.
Прообразами точки
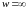 ,
служат корни уравнения
,
служат корни уравнения
 ,
т. е. точка
,
т. е. точка
 .
.
Итак,
многочлен степени
 отображает расширенную комплексную
плоскость на себя так, что каждая конечная
точка образа
имеет
прообразов
отображает расширенную комплексную
плоскость на себя так, что каждая конечная
точка образа
имеет
прообразов
 .
.
Отображение
 является конформным во всех точках, за
исключением точек
является конформным во всех точках, за
исключением точек
 ,
в которых
,
в которых
 ,
а также, за исключением, быть может,
точки
.
,
а также, за исключением, быть может,
точки
.
Если
 ,
то
,
то
 -
целая линейная функция – взаимно
однозначное и конформное отображение
-
целая линейная функция – взаимно
однозначное и конформное отображение
 на
себя.
на
себя.
Степенная функция и радикал
Определение
2.1.
Степенной
называется функция вида
 .
.
Если
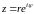 ,
то
,
то
 .
Следовательно,
.
Следовательно,
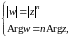

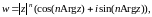
а
значит, функция
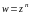 является
многолистной функцией.
является
многолистной функцией.
Степенная
функция
является
аналитической в комплексной плоскости
,
а т.к.
 при
любом
при
любом
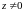 ,
то отображение, осуществляемое этой
функцией, является конформным в каждой
точке
,
то отображение, осуществляемое этой
функцией, является конформным в каждой
точке
 за исключением нуля.
за исключением нуля.
Функция
обладает основными свойствами функции
 действительного переменного, а именно:
действительного переменного, а именно:
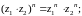

 .
.
Т.к.
многолистная функция, то необходимо
найти области однолистности.
Возьмем
произвольные точки
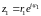 и
и
 такие, что
такие, что
 ,
,
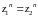 .
Следовательно,
.
Следовательно,
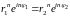 ,
т.е.:
,
т.е.:
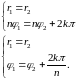
Получили, что
 ,
,
 .
.
Следовательно,
областью однолистности функции
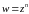 будет любой угол с вершиной в начале
координат и раствором
будет любой угол с вершиной в начале
координат и раствором :
:

Если
 ,
то
,
то
 .
.

Рассмотрим,
в частности, отображение вида
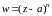 .
Оно является конформным во всех точках,
за исключением точек
.
Оно является конформным во всех точках,
за исключением точек
 и
.
Углы с вершинами в этих точках увеличиваются
при отображении в n
раз.
Заметим, что
и
.
Углы с вершинами в этих точках увеличиваются
при отображении в n
раз.
Заметим, что
 ,
,

Следовательно,
каждая окружность радиуса
 с
центром в точке
отображается на окружность радиуса
с
центром в точке
отображается на окружность радиуса
 с
центром в точке
с
центром в точке
 .
Если при этом точка
пробегает окружность
.
Если при этом точка
пробегает окружность
 один
раз в положительном направлении (т. е.
один
раз в положительном направлении (т. е. ,
непрерывно
возрастая, увеличивается на
,
непрерывно
возрастая, увеличивается на
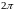 ),
то
точка
),
то
точка
 пробегает окружность
пробегает окружность
 в том же направлении
раз
(т. е.
в том же направлении
раз
(т. е. ,
непрерывно возрастая, увеличивается
на
,
непрерывно возрастая, увеличивается
на
 ).
Если
точка
пробегает
прямолинейный луч
).
Если
точка
пробегает
прямолинейный луч
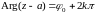 от
точки
от
точки
 до
до
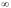 ,
то соответствующая точка
будет пробегать при этом прямолинейный
луч
,
то соответствующая точка
будет пробегать при этом прямолинейный
луч
 от начала координат до бесконечности.
от начала координат до бесконечности.
Итак,
функция
 отображает взаимно однозначно и конформно
внутренность любого угла с прямолинейными
сторонами, вершиной в точке
и раствором
,
отображает взаимно однозначно и конформно
внутренность любого угла с прямолинейными
сторонами, вершиной в точке
и раствором
,
 ,
на
внутренность соответствующего угла
также с прямолинейными сторонами,
вершиной в начале координат и раствором
,
на
внутренность соответствующего угла
также с прямолинейными сторонами,
вершиной в начале координат и раствором
 .
.
К рассматриваемой функции прибегают каждый раз, когда нужно отобразить один угол с прямолинейными сторонами на другой угол, в несколько раз больший.
При
отображении
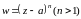 не любая прямая преобразуется в прямую,
окружность — в окружность. Пусть,
например,
не любая прямая преобразуется в прямую,
окружность — в окружность. Пусть,
например, .
Функция примет вид
.
Функция примет вид
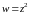 .
Отобразим
прямую, параллельную мнимой оси
.
Отобразим
прямую, параллельную мнимой оси
 ,
,
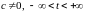 .
В качестве образа получим линию
.
В качестве образа получим линию
 ,
или, полагая
,
или, полагая
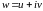 и
отделяя действительные и мнимые
части:
и
отделяя действительные и мнимые
части:
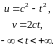
Исключая параметр , получим:
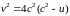 .
.
Это
уравнение параболы с осью, направленной
по действительной оси в отрицательную
сторону, с фокусом в начале координат
и с параметром
 .
.

Аналогично,
отобразим прямую, параллельную
действительной оси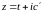 ,
,
 .
В качестве образа получим линию
.
В качестве образа получим линию
 ,
или, полагая
и
отделяя действительные и мнимые
части:
,
или, полагая
и
отделяя действительные и мнимые
части:

Исключая параметр , получим:
 .
.
Т.е. получили, что каждая прямая, параллельная действительной оси , преобразуется в параболу с осью, направленной по действительной оси в положительную сторону, с фокусом в начале координат и с параметром .

Итак, два семейства прямых, параллельных координатным осям, отображаются посредством функции в два семейства парабол с общим фокусом в начале и с осями на действительной оси. Из того, что семейства прямых были взаимно ортогональны, а отображение конформное, вытекает, что и полученные семейства парабол взаимно ортогональны.
Рассмотрим
радикал
 -
функцию обратную к функции
-
функцию обратную к функции
 .
Пусть
.
Пусть
 ,
т.е.
,
т.е.
 ,
тогда
,
тогда
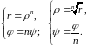
Следовательно,

Получили,
что для любых
и
 радикал имеет
различных значений, которые выражаются
следующей формулой:
радикал имеет
различных значений, которые выражаются
следующей формулой:

Следовательно,
функция
является
многозначной (
–значной).
Эти n
значений
располагаются в вершинах правильного
n
– угольника, вписанного в окружность
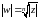 .
При значениях
.
При значениях
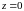 и
и
 получаем по одному значению функции
и
.
получаем по одному значению функции
и
.
Чтобы
выделить однозначную ветвь, достаточно
указать, в какой области
однолистности изменяется
.
Выше было установлено, что областью
однолистности функции
 является
угол с вершиной в начале координат и
раствором
является
угол с вершиной в начале координат и
раствором
 :
:
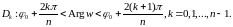
Любой
луч плоскости

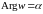 при отображении
переходит в луч плоскости
при отображении
переходит в луч плоскости
 :
:
 .
Если луч
пробегает область
.
Если луч
пробегает область
 против хода часовой стрелки, то луч
пробежит всю плоскость
от
против хода часовой стрелки, то луч
пробежит всю плоскость
от
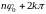 до
до
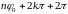 .
Следовательно, любая из областей
однолистности
перейдет в одну и ту же область
плоскости
:
угол раствора
,
границей которой служит луч
.
Следовательно, любая из областей
однолистности
перейдет в одну и ту же область
плоскости
:
угол раствора
,
границей которой служит луч
 .
.
Т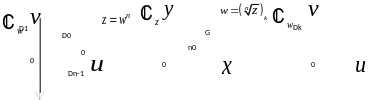 аким
образом, в области
получаем
однозначных ветвей функции
.
Каждая
из них определяется условием, что ее
значения
принадлежат области
.
Будем обозначать эти ветви
аким
образом, в области
получаем
однозначных ветвей функции
.
Каждая
из них определяется условием, что ее
значения
принадлежат области
.
Будем обозначать эти ветви
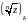 .
.
Т.к.
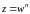 имеет
отличную от нуля производную во всех
точках
имеет
отличную от нуля производную во всех
точках
 ,
то обратные функции
имеют отличные от нуля производные:
,
то обратные функции
имеют отличные от нуля производные:
 .
.
Зафиксируем
какое-либо значение
 .
Пусть точка
описывает в плоскости
.
Пусть точка
описывает в плоскости
 некоторую кривую, содержащую внутри
начало координат. После полного обхода
некоторую кривую, содержащую внутри
начало координат. После полного обхода
 изменится на
(увеличится, если против хода часовой
стрелки и уменьшится, если по ходу).
Следовательно, значение
изменится на
(увеличится, если против хода часовой
стрелки и уменьшится, если по ходу).
Следовательно, значение
 в первом случае перейдет от
к
в первом случае перейдет от
к
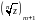 (
( перейдет в
перейдет в
 ),
а во втором – от
к
),
а во втором – от
к
 (
перейдет к
).
(
перейдет к
).
Таким
образом, точка
–
точка разветвления для функции
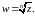 Т.к.
полный поворот от одной ветви многозначной
функции к другой на угол
Т.к.
полный поворот от одной ветви многозначной
функции к другой на угол
 является в то же время и полным оборотом
вокруг точки
(то есть обход по окружности бесконечно
большого радиуса с центром в начале
координат), то
–
тоже точка разветвления.
является в то же время и полным оборотом
вокруг точки
(то есть обход по окружности бесконечно
большого радиуса с центром в начале
координат), то
–
тоже точка разветвления.
Итак,
многозначная функция
 имеет
2 точки разветвления:
и
.
имеет
2 точки разветвления:
и
.
Т.к.
после
-кратного
обхода вокруг этих точек разветвления,
происходит возвращение к исходной
ветви, то точки
и
являются
точками разветвления
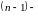 го
порядка функции
го
порядка функции
