2.Дифференцирование функции одной комплексной переменной

Пусть функция определена в окрестности точки . Придадим точке произвольное приращение так, чтобы точка тоже принадлежала окрестности . Тогда функция получит приращение:

.

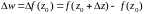Составим отношение

(функция от ).

Определение 2.1. Если существует конечный , то он называется производной функции в точке , и обозначается .

(при любом стремлении точки к точке в комплексной плоскости).

Определение 2.2. Функция называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде:

,

где – комплексное число (не зависит от ), .

Теорема 2.1. Функция дифференцируема в точке тогда и только тогда, когда существует конечная производная функции в точке , причем .

Определение 2.3. (эквивалентно определению 2.2) Функция называется дифференцируемой в точке , если в этой точке она имеет конечную производную.

Теорема 2.2 (необходимое условие дифференцируемости). Если функция дифференцируема в точке , то она непрерывна в этой точке.

Замечание. Обратное неверно. Среди непрерывных функций комплексного переменного существуют функции, которые определены и непрерывны на , но не имеют производной ни в одной точке комплексной плоскости (например ).

Определение 2.4. Функция называется дифференцируемой в области , если она дифференцируема в каждой точке этой области.

Пусть дифференцируема в области . Тогда любой точке , принадлежащей области , можно поставить в соответствие число . Такое соответствие является функцией, которую называют производной функцией от на области . Обозначается .

Теорема 2.3 (необходимое и достаточное условие дифференцируемости функции комплексной переменной). Пусть функция определена в некоторой области . Для того, чтобы функция была дифференцируемой в точке области необходимо и достаточно, чтобы функции и были дифференцируемы в точке как функции двух действительных переменных, и в точке выполнялись равенства:

. (2.1)

При выполнении всех условий теоремы производная может быть представлена в одном из следующих видов:

.

Равенства (2.1) называются условиями Коши-Римана (или Даламбера-Эйлера).

Определение 2.5. Функция называется аналитической (голоморфной, регулярной, правильной) в точке , если она дифференцируема в каждой точке некоторой окрестности точки .

Необходимо различать понятие дифференцируемости в точке и понятие аналитичности в точке: дифференцируема в точке , если существует 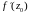; аналитическая функция в точке , если существует окрестность , такая что в любой точке из окрестности точки существует .

Определение 2.6. Функция называется аналитической в области , если она дифференцируема в каждой точке этой области. Таким образом, понятия дифференцируемости и аналитичности в области совпадают.

3. Геометрический смысл аргумента производной

1) Пусть – комплексная функция действительной переменной , заданная на отрезке . Она определяет непрерывную кривую . Пусть существует , для некоторого из отрезка .

Покажем, что тогда в точке кривой , существует касательная , причем угол между и осью совпадает с . Проведем секущую через точки и 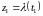, которые принадлежат кривой .

, где , где

Угол между прямой и осью можно определить через . Рассмотрим вектор:

Следовательно,

_.

Значит, направление секущей совпадает с направлением вектора . Поэтому секущая имеет предельное положение, если угол между вектором и осью , равный , имеет предел при , стремящемся к . Т.к существует , то существует и .

Итак, если – комплексно-значная функция действительной переменной имеет производную в некоторой точке , то она имеет касательную в точке . При этом угол наклона касательной к оси равен аргументу производной.

2) Пусть аналитическая в некоторой области G функция, причем принадлежит области .

Проведем через точку кривую , где принадлежит отрезку , . Т.к. существует , то в точке существует касательная с углом наклона . При отображении кривая перейдет в кривую , расположенную в плоскости . Кривую можно представить в виде . По правилу дифференцирования сложной функции существует . Следовательно, и у кривой в точке существует касательная, причем угол между касательной и осью равен:

Отсюда:

(3.1)

величина, на которую изменяется угол наклона касательной при переходе от кривой к кривой .

Итак, геометрический смысл аргумента производной состоит в следующем: аргумент производной в точке равен углу поворота касательной к кривой в точке при переходе к её образу и к точке .

Рассмотрим теперь две кривые и , проходящие через точку . Обозначим через и углы наклона касательных к ним в точке . Образами кривых и являются кривые и с углами наклона в точке и . Из выражения (3.1) следует, что:

.

Следовательно,

.

Таким образом, отображение , где аналитическая в точке функция и сохраняет углы между кривыми, проходящими через точку , при этом сохраняется не только величины, но и направление отсчета.