§ 3. Квадратичные формы

11. Квадратичные формы. Квадратичной формой от нескольких переменных называется однородный многочлен второй степени от этих переменных. Например, квадратичная форма от трех переменных

x_lt х₂, x_s в общем случае имеет вид

/=•= а_их\ + a_zzx\ + а_зах! + 2а₁₂*₁х_! + 2а₁₃л;₁лг₃ + 2а_м*,*₈, (39)

где а_ц, я_2а, ..., а₂₃— некоторые числовые коэффициенты (а двойки поставлены для упрощения получающихся формул). Матрицей такой формы называется симметрическая матрица

С помощью этой матрицы форму (39) можно переписать в виде F = (вц*! + а_пх₂ + а₁₃х_&) x_t + (a_nXi + а₂₂лг_а + а.,₃х₃) x_z +

v

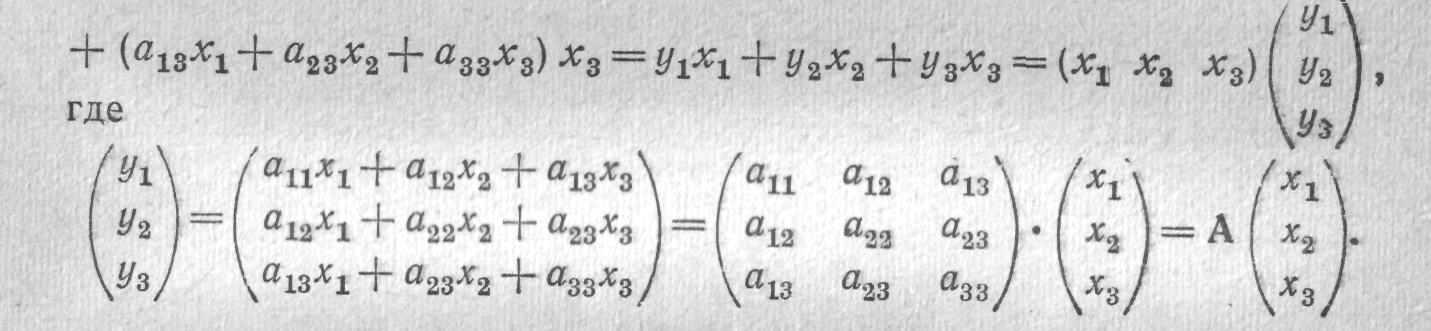
Значит, если ввести числовой вектор

то получим

W F = x*Ax. (40)

Обратно, если форма представлена в виде (40), причем матрица А симметрическая, то А является матрицей этой формы.

Проведем теперь какую угодно линейную замену переменных вида (30) или, коротко,

х = Нх'. (41)

Тогда в силу формулы (4) х*=х'*Н*, откуда

F = х'*Н*АНх' = х'* (Н*АН) х',

т. е.

/^г=х'*А'х', где А' = Н*АН. (42)

Однако матрица А' симметрическая, так как в силу формулы (4) А'* = (Н*АН)* = Н*А*Н** = Н* АН = А'.

Значит, А' и служит матрицей квадратичной формы после замены переменных.

Итак, при подстановке (41) матрица квадратичной формы пре­образуется по формуле (42). Если, в частности, считать матрицу Н ортогональной, то в силу формулы (34) получаем, что А' = Н~^ТАН. Как было показано в п. 10, всегда можно подобрать матрицу Н

так, чтобы A'=dlag (А^Дз, ^sK где на диагонали стоят собственные-значения матрицы А. Но тогда квадратичная форма F в новых пе­ременных приобретает диагональный вид

F = K₁x'₁* + b_tx'S + b_tx'_t*. (43)

Итак, квадратичную форму (39) можно с помощью преобразования (30) с ортогональной матрицей привести к диагональному виду (43), где K_t, K%, A,₈ — собственные значения матрицы А.

Указанное формальное преобразование имеет следующий геомет­рический смысл. Рассмотрим матрицу А как матрицу некоторого линейного преобразования А в декартовом базисе с координатами ^xi> ^Х2> ^хз- Тогда переход (41), приводящий квадратичную форму F к виду (43), отвечает переходу к новому базису, составленному из собственных векторов преобразования А.

В п. 8 (формула (33)) мы показали, что при любой замене вида (31) оп­ределитель det(A—Kl) не меняется. Значит, если разложить этот определитель по степеням X, то коэффициенты при этих степенях также не будут меняться; эти коэффициенты будут инвариантными относительно замены декартовых координат. Например, квадратичная форма от двух переменных при обоз­начениях, принятых в аналитической геометрии, имеет вид

Ах² + 2Вху + Су*, т. е. ее матрица такова:

а характеристическое уравнение

Значит, выражения А-\-С и АС — В^а инвариантны относительно замены де­картовых координат (см. п. 11.13).

12. Упрощение уравнений линий и поверхностей второго по­рядка. Преобразование квадратичной формы, описанное в п. 11, применяется, в частности, к упрощению уравнений линий и поверх­ностей второго порядка. Остановимся на уравнении поверхностей, так как упрощение уравнений линий второго порядка описано в п. 11.13.

Пусть поверхность второго порядка задана в обычном для ана­литической геометрии виде (Х.13). Переход к новой декартовой системе координат с тем же началом, как было показано в п. 9, сводится к замене переменных

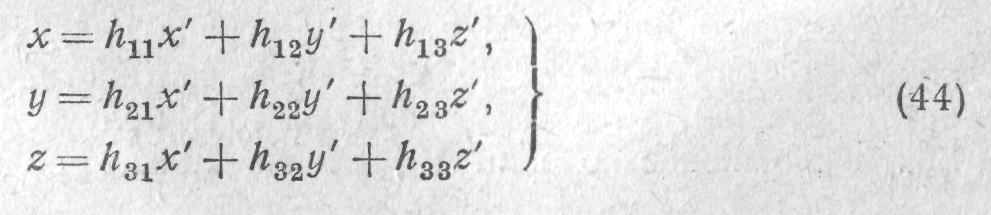
с ортогональной матрицей перехода Н. (Ясно, что если начало ко­ординат не заменяется, то координаты точек преобразуются по тем же формулам, что координаты векторов.) При подстановке этих выражений в уравнение (Х.13) группа членов второй степени и группа членов первой степени преобразуются независимо друг от друга. Если следить сначала только за группой членов второй сте­пени (квадратичной формой), то на основании п. 9, мы получаем, что всегда можно выбрать систему координат х', у', z' так, что эта группа членов приобретет диагональный вид. Поэтому все уравнение после преобразования будет иметь вид

V<r'² + b_zy'* + V» + G'x' + H'y'+ I'z' + J =* 0; (45)

здесь K_lt К_г, К₃ — корни уравнения

а О', Н', /'—некоторые новые коэффициенты при членах первой степени, которые сами получатся после подстановки (44). Уравне­ние (45) — это уравнение (Х.14) в других обозначениях; его иссле­дование описано в п. Х.11.