МАТРИЦЫ И ИХ ПРИМЕНЕНИЕ

Матрицы

Матрицы, впервые появившиеся в середине прошлого века в ра­ботах английских математиков У. Гамильтона (1805—1865) и А. Кэли (1821—1895), в настоящее время в прикладной математике исполь­зуются весьма широко, они значительно упрощают рассмотрение сложных систем уравнений.

Матрицей называется прямоугольная таблица, составленная из чисел или каких-либо других объектов. Такая матрица может иметь, например, вид

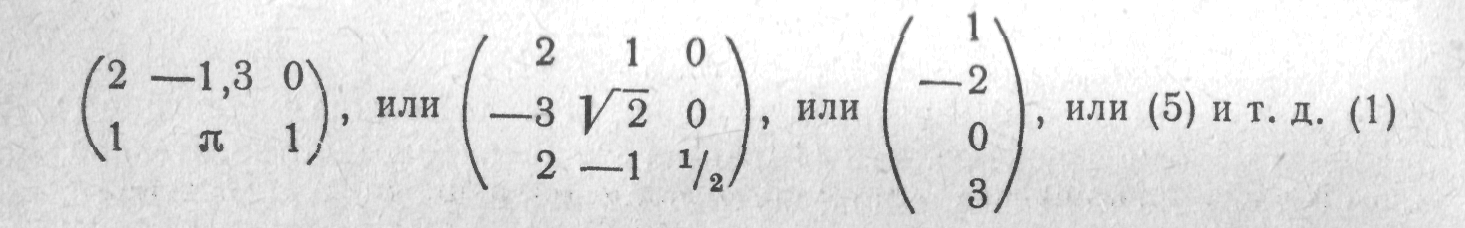
Здесь круглые скобки по бокам—знак матрицы; применяются также волнистые вертикальные линии, но, конечно, не простые вертикаль­ные черточки, которыми обозначается определитель (§ VI. 1). Как у определителей, у матриц различают элементы, строчки и столбцы. Однако важнейшим отличием от определителей является то, что определитель считается ранным некоторому числу (и. VI.1), тогда как матрица не приравнивается какому-либо более простому объекту. Ее можно для краткости обозначить одной буквой, например А, В и т. п., но тогда под А все равно будет пониматься таблица. В об-

щем виде

Таким образом, элементы матрицы удобно снабжать двумя индексами, из которых первый указывает номер строки, а второй — номер столбца. Иногда коротко пишут А~(а^}_тп, "т. е. / меняется от 1 до до, a j—от 1 до п. , .

Каждая матрица имеет определенные размеры, т. е. количество строк и количество столбцов; так, в строках (1) и (2) выписаны матрицы соответственно размера 2x3, 3x3, 4x1, 1x1, тХп. Если число строк равно числу столбцов, то матрица называется квадратной, тогда говорят о ее порядке. Квадратная матрица первого порядка отождествляется со своим единственным элементом; так, четвертая матрица (1)—это просто число 5.

Матрица, у которой всего один столбец, называется столбцевой, или числовым вектором; такая матрица отождествляется с вектором в вещественном числовом пространстве (п. VII.18). Так, третья ма­трица (1) — это вектор в Ец с координатами 1; —2; 0; 3. Матрица, у которой всего одна строка, называется строчной,

Матрица, у которой все элементы равны нулю, называется нуле­вой. Квадратная матрица, у которой равны нулю все элементы, кроме, быть может, стоящих на главной диагонали (т. е. диагонали, идущей из левого верхнего в правый нижний угол), называется диагональной; если на диагонали стоят элементы а, Ь, ..., k, то матрица обозна­чается diag (а, Ь, ..., k). Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной и обычно обозначается буквой I: например, единичная матрица третьего порядка имеет вид

Иногда применяется транспонирование матрицы А, т. е. перемена ролями ее строк и столбцов (ср. п. VI.2); полученную матрицу мы обозначим А*. Например,

в общем виде можно написать а*/ = а_/(. (почему?). Ясно, что (А*)* = А.

Матрица, совпадающая со своей транспонированной, называется симметрической; такой может быть только квадратная матрица. Условие симметричности можно записать в виде 6^ = ^,..

Если uij— —ац, то матрица называется кососиммепгрической.

Квадратная матрица А имеет определитель, который мы будем

обозначать det А; например, detj 1= =—3. Прямо-

\.2 —Зу 2 —3

угольная неквадратная матрица определителя не имеет, так как опре­делители бывают только квадратные. Из п. VI.2 следует, что

det i=l, det A* = det A.

2. Действия йад матрицами. Матрицы одинакового размера можно складывать по формуле

аналогично определяется умножение матрицы на число:

Легко проверить, что при этом выполняются все аксиомы линейных действий (п. VII.17), т. е. совокупность всех матриц одинакового размера образует линейное пространство. Отмстим очевидные формулы:

(А + В)* = А* + В*; (АА)* = *А*; dot (AC) = k" det С,

где п — порядок квадратной матрицы С. При этом, вообще говоря det (А + В) Ф det A + det В.

Умножение матриц друг на друга осуществляется по своеобраз­ному закону, разумность которого будет ясна из п. 6. Прежде всего, размеры матриц-сомножителей должны быть согласованы: ширина первого множителя должна равняться высоте второго, в противном случае умножение невозможно. Если же это условие выполнено, то произведение находится по следующему правилу:

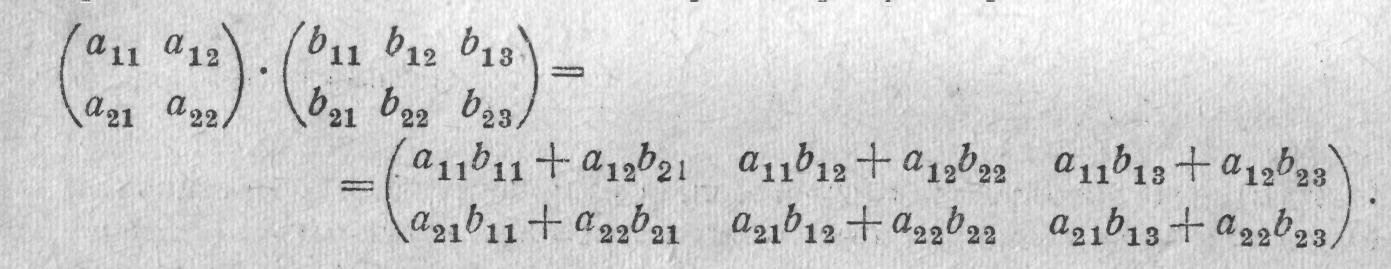
Надо внимательно продумать это правило. Например, чтобы получить у произведения элемент, стоящий в первой строке и в третьем столбце, надо у первого множителя взять'первую строку, у второго—третий столбец, а затем эти строку и столбец как бы скалярио перемножить (см. формулу (VII. 12)). И другие элементы матрицы-произведения получаются с помощью диалогичного «как бы скалярного умножения» строк первой лшгрмчы-множителя ^на столбцы второй .матрицы-множи­теля. В общем случае, если мы умножим матрицу (а,-.) размера тхп на матрицу (Ьц) размера яхр, мы получим матрицу (с,у) размера

п

тХр, элементы которой вычисляются по формуле с,, = 2 ^а,-А/-

к — 1

Из приведенного правила вытекает, что всегда возможно перемно­жить две квадратные матрицы одинакового порядка, что даст квад­ратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т. е. возвысить в квадрат, тогда как прямоугольную неквадратную матрицу возвысить в квадрат нельзя. Другим важным частным случаем является умножение строч-

ной матрицы на столбцевую, причем ширина первой равна высоте второй; это даст квадратную матрицу первого порядка, т. е. число

Аналогично п. VI.2 можно проверить следующие свойства про­изведения матриц:

(feA)B = A(£B)=fc(AB); (А + В) С = АС + ВС;

С(А + В)=СА + СВ; А (ВС) = (АВ) С;

конечно, при этом всегда подразумевается, что размеры участвующих здесь матриц обеспечивают осмысленность формулы. Другой метод вывода этих формул будет указан в п. 6.

Уже на самых простых примерах легко проверить, что матрицы, вообще говоря, не перестановочны друг с другом, т. е., вообще говоря, АВ^ВА. Например (проверьте!)

Поэтому при умножении матриц надо тщательно следить за порядком множителей; для этого применяются термины: «умножим А справа на В» или просто «умножим А на В» (получится АВ), но «умножим А слева на В» (получится ВА).

Отметим еще непосредственно проверяемое свойство

(АВ)* = В* А* (4)

и свойство, которое будет доказано в п. 7,

det(AB)=detA'detB. (5)

Если А—комплексная числовая матрица, то под А* понимается резуль­тат транспонирования с одновременной заменой всех элементов на их комп­лексно сопряженные значения; при этом А* называется матрицей, сопряженной с А. Для комплексных матриц из приведенных выше формул надо изменить только две: det А* = (det А)*, (ЛА)* = Л*А*.

3. Обратная матрица. Будем рассматривать квадратные матрицы некоторого определенного, например третьего, порядка. При умноже­нии таких матриц единичная матрица (3) играет ту же роль, что единица при умножении чисел: легко непосредственно проверить,, что AI — 1А = А для любой матрицы А.

ч-----

По аналогии с умножением чисел определяется и понятие обратной к А матрицы: это матрица А"¹, для которой

А~¹А = АА-¹ = 1. (6)

Отсюда и из равенства (5) вытекает, что

Мы видим, что обязательно должно быть det A =^= 0. Квадратная матрица А, для которой det А = 0, называется вырожденной. Таким образом, вырожденная матрица не имеет обратной. В то же время всякая невырожденная матрица имеет обратную. В самом деле, рас­смотрим любую невырожденную матрицу

Тогда, исходя из определения произведения матриц и рассуждая, как в п. VI.4, легко проверить, что произведение К слева или справа на матрицу

равно I; здесь большими буквами А_ъ ... , С₃ обозначены алгебраи­ческие дополнения соответствующих элементов в матрице К (или, что то же, в соответствующем определителе, см. п. VI.3). Значит, мат­рица (8) и есть К"¹.

Обратные матрицы применяются при решении матричных уравне­ний. Например, рассмотрим уравнение АХ = В, где АиВ — заданные матрицы, а X — искомая, причем detA=^0. Умножив обе части слева на А~' и воспользовавшись равенствами (О), получаем Х = А^-1В. Аналогично из уравнения ХА — В получаем решение Х = ВА^-1.

Матрицы дают возможность кратко записать систему уравнений первой степени. Например, систему уравнений (VI.5) можно пере­писать в матричной форме

(проверьте!). Если обозначить матрицу коэффициентов буквой А, столбец (т. с. числовой вектор) неизвестных буквой х, а столбец свободных членов буквой 4, то то же уравнение можно еще короче за­писать в виде

Ах = d, (9)

§ 1] Матрицы 279

откуда при det А Ф 0 сразу получаем решение

x = A~¹d. .(10)

Конечно, если подробно расшифровать эту формулу, получится то же правило Крамера, которое было найдено в п. VI.4. Отметим, что запись (9) возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица А не будет квадратной; однако при этом нельзя перейти к формуле (10), так как неквадратная матрица не имеет обратной.

Из формул (6) видно, что матрицы А и А"¹ являются взаимно обрат; ными, т. е. (А~¹)~¹ = А. Кроме этой, иногда применяется формула (АВ)"¹™ = В~¹А~¹ (det А т= 0, det В ф 0), которую легко проверить: (В~¹А~¹) (АВ)= = В-¹(А~¹А)В =В-ЧВ = В~¹В=1.

Наконец, из формулы (4), если подставить В = А~¹, вытекает, что (А" ¹)*А* = (АА-¹)* = !* = !, т. е. (А-¹)* = (А*)-¹.

4. Собственные векторы и собственные значения матрицы.

Пусть А — заданная квадратная матрица. Как мы увидим позже, иногда приходится рассматривать уравнение

Ах = Ал, (11)

где х — неизвестный числовой вектор, высота которого равна порядку А, а К — неизвестное число. При любом К уравнение (11) обладает, в частности, тривиальным решением х = 0, однако нас будут интере­совать только такие К, при которых эта система имеет нетривиальные решения. Эти значения А, называются собственными, значениями мат­рицы А, а решения х уравнения (11) при таких X — ее собствен~ ными векторами.

Собственные значения и собственные векторы находятся следую­щим образом. Так как х = 1х, то уравнение (11) можно переписать в виде

(А — М)х = 0. (12)

Сравнивая с формулой (9), видим, что получилась система из л алге­браических линейных однородных уравнений с п неизвестными, где п — порядок матрицы А. Согласно п. VI.6 для наличия нетривиального решения необходимо и достаточно, чтобы определитель системы рав­нялся нулю, т. е.

det (A — XI) =0. (13)

Это уравнение называется характеристическим уравнением, мат­рицы А, оно служит для разыскания собственных значений Я. Так, для матрицы (7) оно имеет вид

Раскрыв определитель, мы видим, что получается алгебраическое уравнение, степень которого равна порядку матрицы А. В силу п. VIII.8 заключаем, что матрица порядка п имеет п собственных значений, среди которых, правда, могут быть совпадающие.

Найдя какое-либо собственное значение, мы можем соответствую­щие собственные векторы найти из векторного уравнения (12) (пере­писанного в виде системы скалярных уравнений), как указано в п. VI. 6. Из уравнения (12) вытекает, что при зафиксированном Я. сумма решений y = x^j-fx² будет снова решением и произведение у = £х решения на число будет также решением того же уравнения. Значит, совокупность всех собственных векторов, отвечающих заданному соб­ственному значению, образует линейное подпространство (п. VII.18) пространства всех числовых векторов заданной высоты п.

В наиболее важном случае, когда псе собственные значения различные, каждое из этих подпространств одномерное, т. е. для каждого собственного значения соответствующий собственный вектор определен с точностью до чи­слового множителя. При этом имеются в виду комплексная размерность и комплексные собственные векторы, так как вещественное .характеристическое уравнение (13) может иметь как вещественные, так и мнимые корни. Указанная одномерность вытекает из того, что ненулевые собственные векторы, отвечающие-различным собственным значениям, обязательно линейно независимы, а в «-мер­ном пространстве числовых векторов не может быть более л линейно незави­симых векторов. А эта линейная независимость проверяется так: если, на­пример, собственные векторы х¹, х², х³ отнеч.чюг рачлнчпым собственным значениям К_г, А.₂, А_;|, причем х¹ с х² линейно пмаписнмы, а х^я = ах'-|-рх², то, помножив это равенство справа на А, получаем А,_ах³ = аХ₁х¹-|-р^2^х2> откуда, умножив первое равенство на Ji_g и вычитая, выводим и (^—К₃)х¹ + + Р (Х₂—А,₃) х² = 0, чему противоречит линейная независимость х¹ и х².

Если имеются совпадающие собственные значения, то можно проверить, что для каждого собственного значения "k^ кратности n_k подпространство собственных векторов имеет размерность m_k^n_k. Если все т^ — п/,, то, вы­брав базис в каждом из этих подпространств, мы получаем базис в комплекс­ном числовом пространстве Z_n, состоящий из собственных векторов матрицы А, имеющей поряДок « (если все К/, вещественные, получаем базис в Е„). Если хотя бы одно т^ < п^, то базиса из собственных векторов матрицы А указать нельзя.

5. Ранг матрицы. Вычеркнем ни матрицы А несколько строк и столбцов так, чтобы количество оставшихся строк равнялось коли­честву оставшихся столбцов. Если после этого заменить знак матрицы на знак определителя, то полученный определитель называется ми­нором матрицы А. Матрица имеет много миноров, причем некоторые из них могут равняться нулю, а другие отличны от нуля, Наивысший из порядков миноров, отличных от нуля, называется рангом матрицы А, это очень важная ее характеристика. Например, у матрицы

все три минора второго порядка

равны нулю, тогда как среди шести миноров первого порядка

имеется четыре отличных от нуля. (Определитель первого порядка

принимается равным своему единственному элементу.) Поэтому rang B = l. Мы предоставляем читателю проверить, что ранги матриц

равны соответственно 2, 3, 2, 1, 1. Ранг нулевой матрицы, у кото­рой вовсе нет миноров, отличных от нуля, принимается равным нулю. Ясно, что ранг квадратной матрицы не превосходит ее порядок; ранг равен порядку в том и только том случае, если матрица невырожденная. Ранг матрицы размера тХп, где т^п, не превос­ходит меньшего из чисел тип.

Можно доказать, на чем мы не будем останавливаться, что ранг матрицы равен максимально возможному числу ее линейно независимых строк. (Отме­тим, что строки матрицы сами являются матрицами, т. е. над ними возможно производить линейные действия.) Так, во втором примере (Г4) все три строки линейно независимы; в третьем примере первые две строки линейно незави­симые, а третья равна их сумме; в четвертом примере вторая и третья строки линейно выражаются через первую.

Из свойства 7 п. VI.2 сразу следует, что у транспонированных матриц ранги одинаковы. Поэтому ранг одновременно равен максимально возможному числу линейно независимых столбцов матрицы.

С помощью понятия ранга формулируются окончательные теоремы о раз­решимости систем линейных алгебраических уравнений, даже если число урав­нений не равно числу неизвестных. Рассмотрим для определенности систему из трех уравнений с четырьмя неизвестными

Если ввести числовые векторы

то систему (15) можно переписать в виде

f = xa-fi/b + zc-fud, (16)

т. е. задача сводится к разложению заданного вектора f по четырем заданным векторам а, Ь, с, d. Когда это возможно? Все векторы вида xa-j-j/b-fzc-fud при заданных а, Ь, с, d и всевозможных х, у, г, и образуют линейное под­пространство в Е₃, «натянутое» на а, Ь, с, d. Размерность этого подпростран­ства в силу леммы п. VII.19 равна максимальному числу k линейно незави­симых векторов среди а, Ь, с, d, т. е. рангу матрицы А коэффициентов системы (15). Для разложимости (16) нужно, чтобы вектор f лежал в указан­ном подпространстве, т. е. чтобы среди векторов а, Ь, с, d, f было также только k линейно независимых. Итак, получаем необходимое и достаточное условие существования решения системы (15):

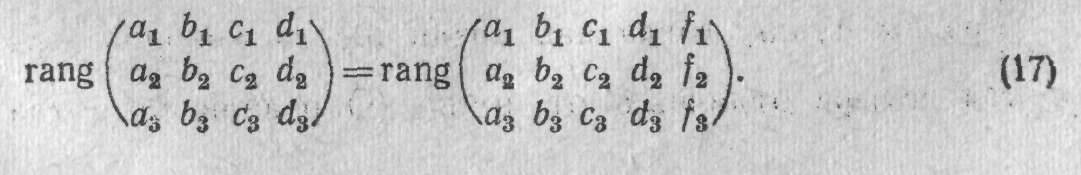
Аналогичный вид имеет условие разрешимости для любого числа уравнений и неизвестных.

Пусть теперь условие разрешимости (17) выполнено; сколько тогда ре­шений имеет система (15)? Если обозначить через х_й, у₀, г₀, и₀ какое-либо одно решение этой системы и ввести замену переменных х — х₀-{-х', ..., и = = «о + «'> то легко проверить, что х', у', г', и' должны удовлетворять соот­ветствующей однородной системе

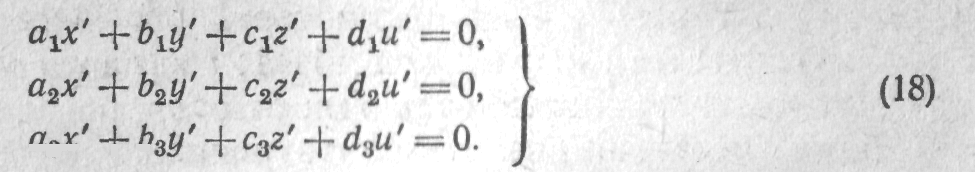
«_а— i «

Введем в £₄ числовые векторы

Тогда в силу п. VII.20—21 систему (18) можно переписать в виде

Pi-x'^0, р_а-х' = 0, р₃-х' = 0. (19)

Таким образом, искомый вектор х' должен быть перпендикулярен к подпро­странству в Е&, «натянутому» на р_х, р₂, р₃. Размерность этого подпростран­ства равна рангу (17), а потому нетрудно проверить, что размерность линей­ного подпространства векторов х' равна 4—rang А (в общем случае вместо 4 должно быть число неизвестных). Такой же получается и ра.шерность сово­купности решений системы (19); если каждое решение рассматривать как набор координат точки в E_t,^io получается, что при выполнении условия (17) совокупность решений системы (15) определяет в £₄ гиперплоскость (п. VII. 19) размерности 4 — rang А.