Нахождение опорного решения

Если в таблице (2.1.3) все элементы столбца свободных членов неотрицательны ( ), то точка таблицы (с координатами ) является опорным решением, так как для нее , и, следовательно, все , и система (2.1.2) удовлетворяется.

Если же в таблице (2.1.3) хотя бы один свободный член отрицателен (например, - й, где ), то в точке таблицы и, следовательно, она не является решением систем (2.1.5) и (2.1.2).

Переход от текущей таблицы к следующей, содержащей меньшее (в общем случае – не большее) число отрицательных свободных членов, осуществляется посредством МЖИ с разрешающим элементом, выбор которого производится по следующему правилу:

1) Находим строку (первую попавшуюся) с отрицательным элементом столбца свободных членов (если таковой не оказалось, то опорное решение уже найдено, и следует переходить к поиску оптимального решения). Пусть, например, ;

2) среди коэффициентов этой строки находим первый попавшийся отрицательный (если такового не оказалось, то система ограничений ЛП-задачи противоречива). Пусть, например, , т.е. s-й столбец - разрешающий;

3) для выбора разрешающей строки находим минимальное неотрицательное среди отношений элементов столбца свободных членов к соответствующим отличным от нуля коэффициентам разрешающего столбца (назовем его МНО). Пусть МНО достигается при , т.е.

.

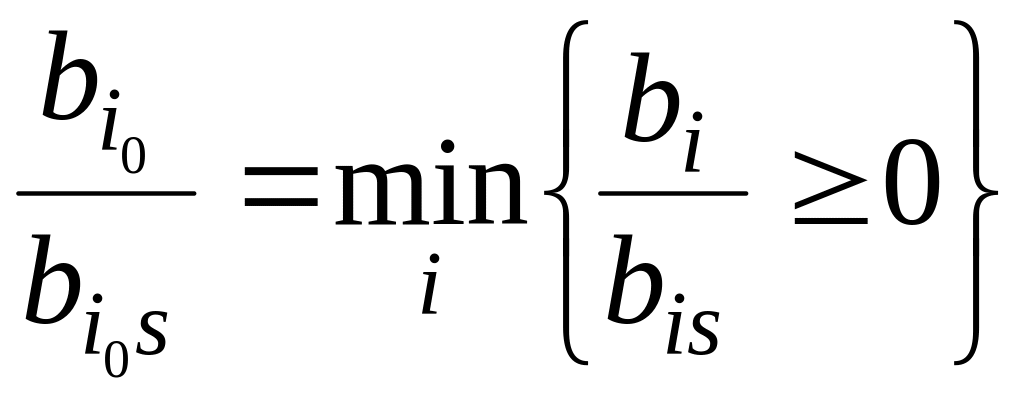Тогда -ю строку берем в качестве разрешающей, так что - разрешающий элемент.

Примечание. Если часть свободных членов равна нулю, то говорят, что имеет место вырождение. При этом МНО 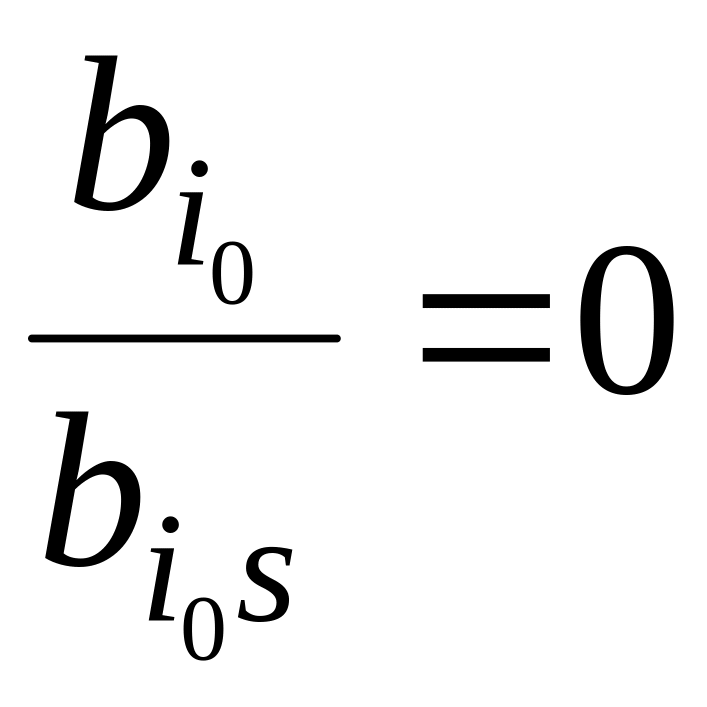. Коэффициент следует брать в качестве разрешающего лишь при , в противном случае ищем новое МНО, не учитывая -ю строку.

Если разрешающим оказался , то после шага МЖИ новый свободный член станет положительным.

Если же разрешающий элемент не попал в r-ю строку, то новый (свободный член в r-й строке после МЖИ) останется еще отрицательным, но уменьшится по модулю. В этом случае продолжаем работать с r-й строкой (делать МЖИ, выбирая разрешающий элемент по изложенному правилу), и либо станет неотрицательным, либо установим несовместность системы ограничений.

Точка таблицы с неотрицательным столбцом свободных членов и будет соответствовать опорному решению.

Поиск оптимального решения (решение задачи максимизации)

В зависимости от знаков коэффициентов Z-строки в таблице, полученной после отыскания опорного решения, возможны два случая.

1. Все коэффициенты Z-строки неотрицательны.

Если , то задача линейного программирования решена, причем и достигается в точке . Действительно, в этой точке имеем , т.е. удовлетворяются ограничения (2.1.2), и так как в любой другой точке многогранника  все неотрицательны, то , т.е. - максимальное значение .

2. Среди коэффициентов Z-строки есть отрицательные.

Пусть . В этом случае нельзя утверждать, что значение функции в точке P₀ с координатами является максимальным. Чтобы осуществить переход от точки P₀ к соседней вершине многогранника  с большим (не меньшим) значением , необходимо произвести шаг МЖИ с разрешающим элементом, выбранным по следующему правилу:

1) Находим столбец (первый попавшийся) с отрицательным коэффициентом Z-строки (если таковых не окажется, то задача уже решена). Пусть, например, , т.е. s-й столбец ‑ разрешающий;

2) для выбора разрешающей строки находим МНО, используя процедуру выполнения п. 3 правила выбора разрешающего элемента при поиске опорного решения (при поиске оптимального решения, в отличие от поиска опорного, МНО может не существовать, если в s-м столбце не оказалось положительных элементов — это означает неограниченность сверху функции цели Z). Пусть МНО достигается при , т.е.

.

Тогда -ю строку берем в качестве разрешающей, так что  ‑ разрешающий элемент.

Примечание. Если МНО , то коэффициент можно брать в качестве разрешающего лишь при , в противном случае ищем новое МНО, не учитывая -ю строку.

После шага МЖИ с разрешающим элементом коэффициент станет положительным (при этом возможно появление новых отрицательных коэффициентов в Z-строке).

Если все новые коэффициенты Z-строки неотрицательны, то задача решена.