43

Лабораторная работа № 2 Тема: «Симплекс-метод решения задачи линейного программирования»

Цель работы: используя модифицированные жордановы исключения (МЖИ), найти опорное и оптимальное решение задачи линейного программирования симплекс-методом.

Содержание отчета

1. Условие лабораторной работы (постановка задачи).

2. Исходная таблица.

3. Все таблицы МЖИ, полученные при нахождении опорного решения.

4. Опорное решение.

5. Все таблицы МЖИ, полученные при нахождении оптимального решения.

6. Оптимальное решение.

7. Текст программы.

8. Экранные формы.

Теоретические сведения

Основная задача линейного программирования заключается в отыскании максимума (минимума) линейной формы (называемой целевой функцией)

(2.1.1)

при выполнении ограничений (системы линейных неравенств)

которые перепишем в виде

. (2.1.2)

Найти максимум (минимум) формы (2.1.1) при выполнении условий (2.1.2).

Другими словами, среди решений системы (2.1.2) (образующих допустимую область ), надо отыскать такое, для которого линейная форма (2.1.1) принимает наибольшее (наименьшее) значение.

Симплекс-метод состоит из алгоритма отыскания опорного решения системы линейных неравенств (2.1.2), т.е. определения координат любой вершины многогранника  (или установления факта несовместности системы), и алгоритма направленного перехода от полученного опорного решения к оптимальному – вершине с максимальным (минимальным) значением функции цели (2.1.1). Основу вычислительной схемы симплекс-метода составляют модифицированные жордановы исключения (МЖИ).

Определение 1. В некоторых приложениях вычислительного аппарата жордановых исключений, например, в симплекс-методе, важно, чтобы элементы разрешающей строки сохраняли знаки, а элементы разрешающего столбца меняли их на противоположные. В этих случаях вместо обыкновенных пользуются так называемыми модифицированными жордановыми исключениями.

Запишем систему (1.1.1) в виде

,

или в виде таблицы:

		...		...
		...		...
...	.	.	.	.	.
		...		...		,
...	.	.	.	.	.
		...		...

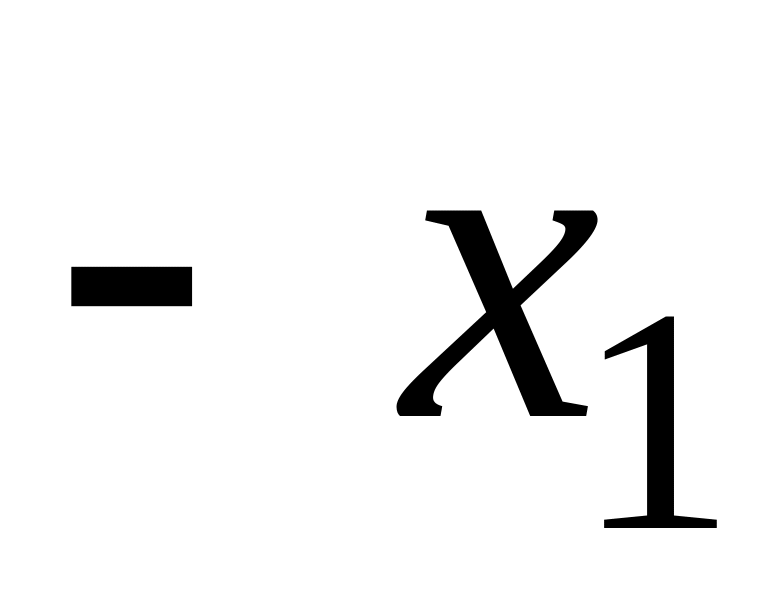
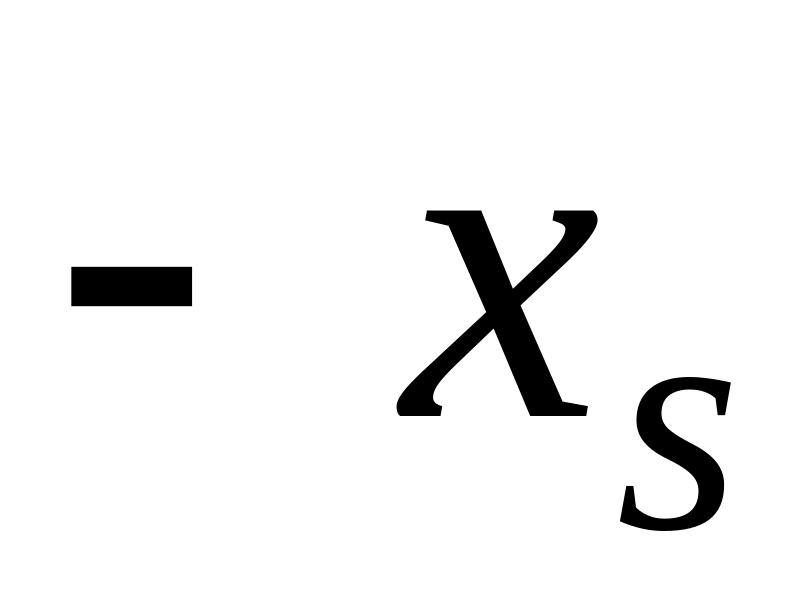
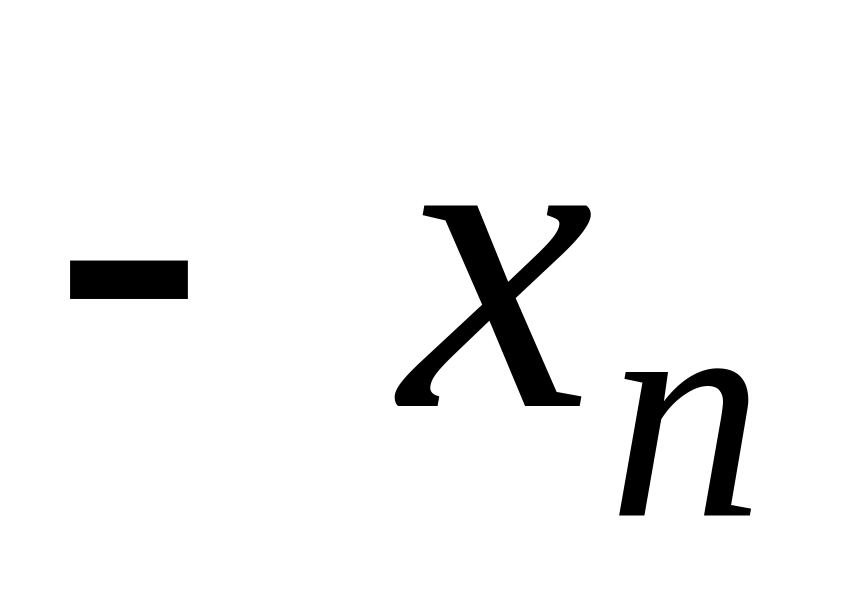
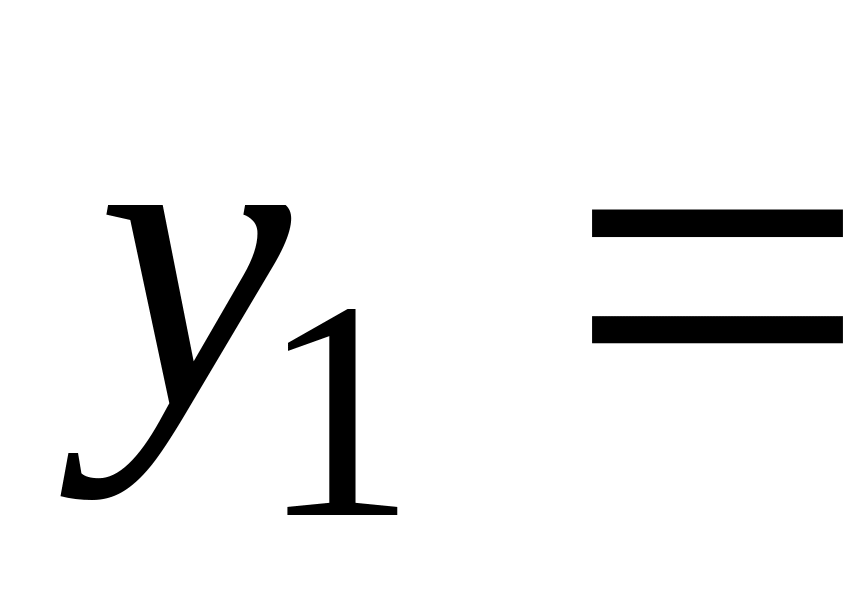
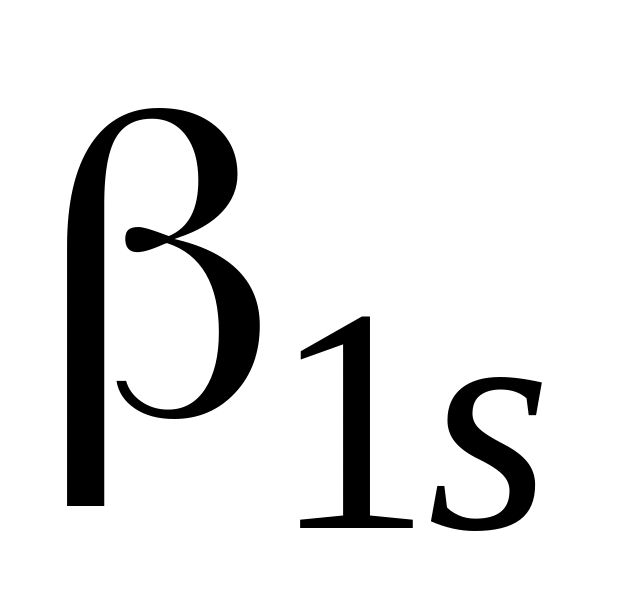
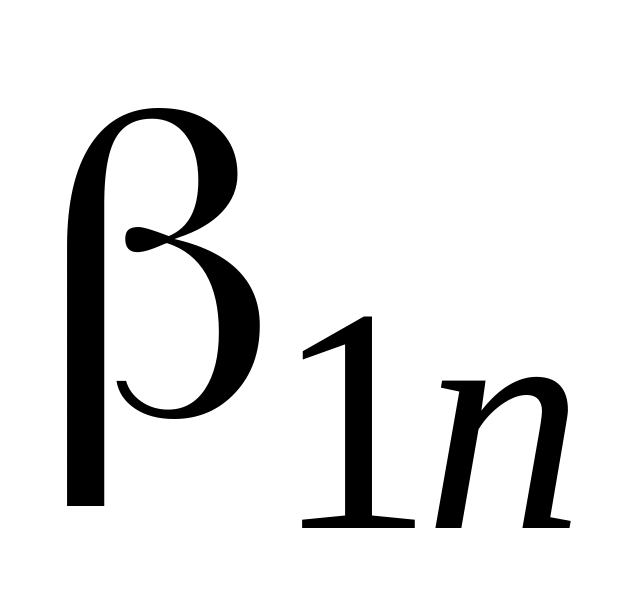
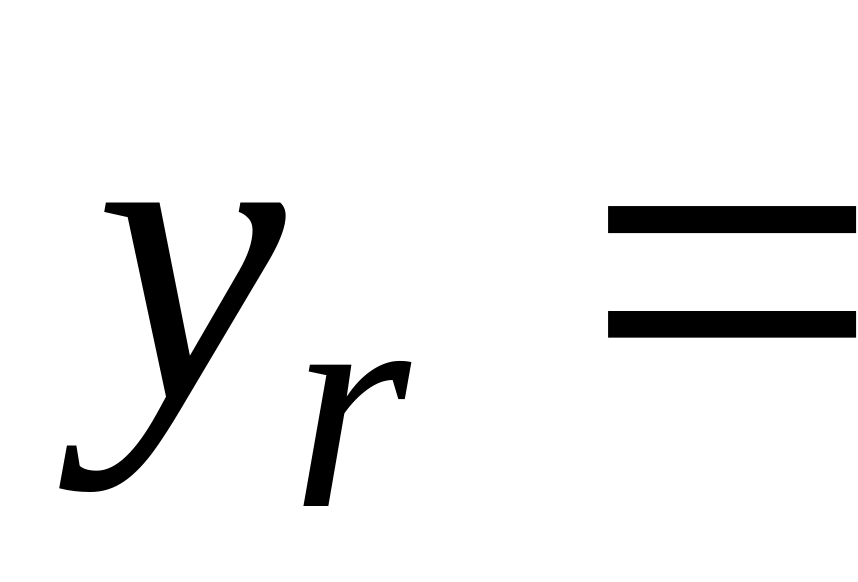
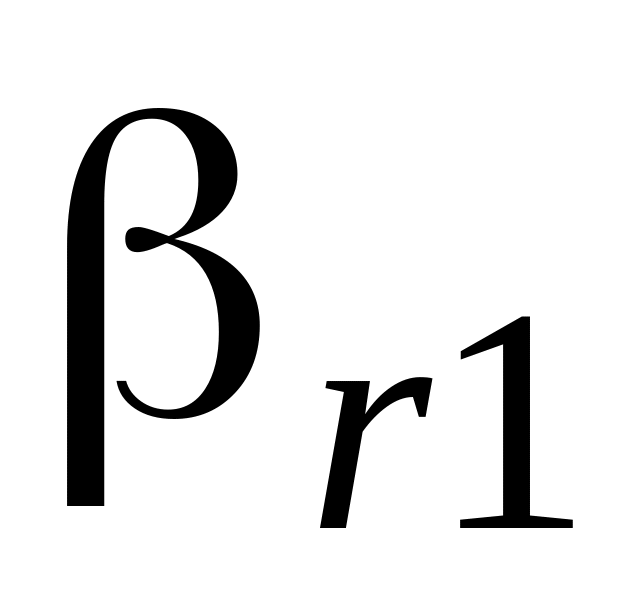
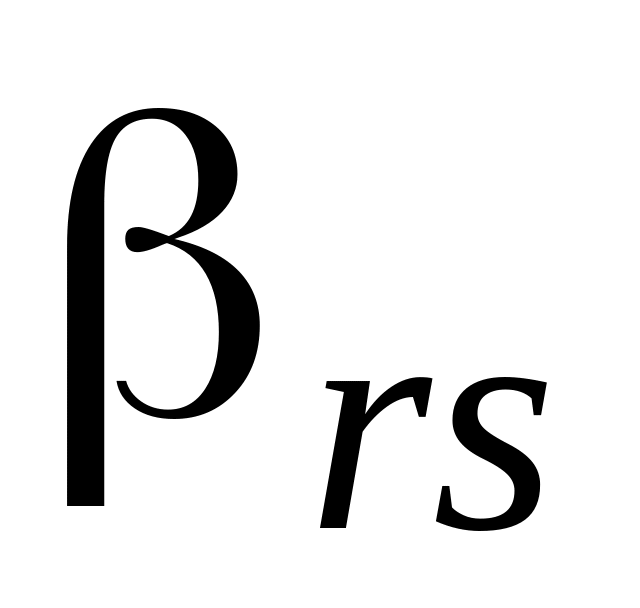
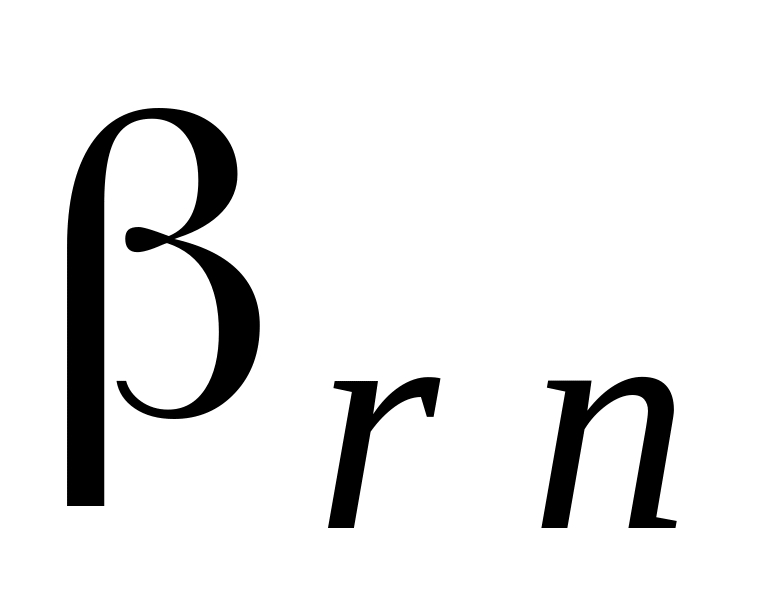
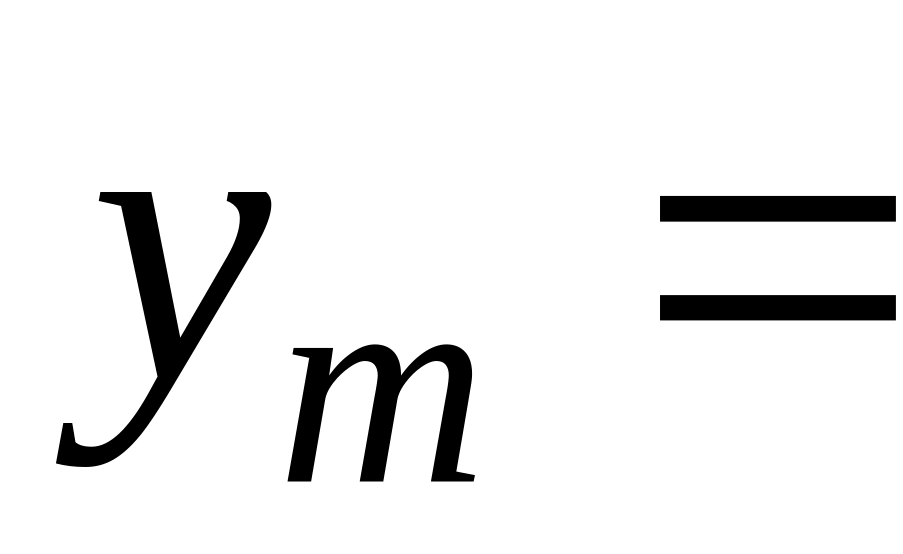
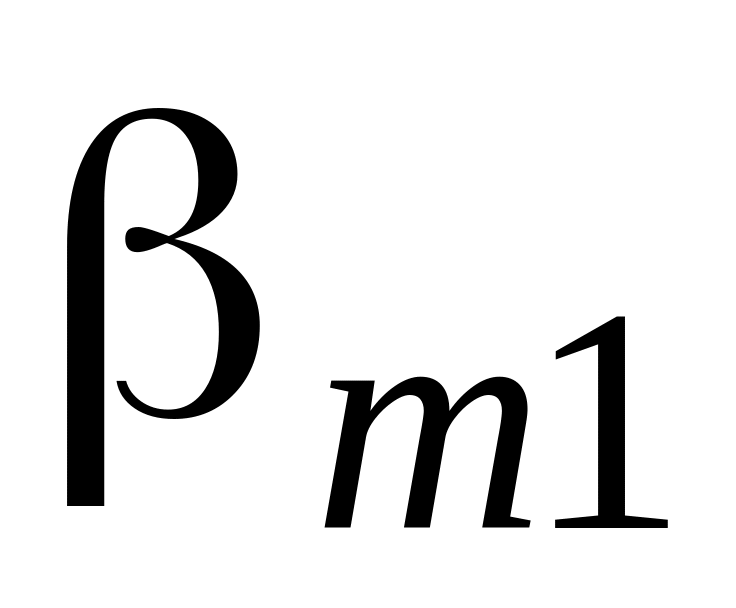
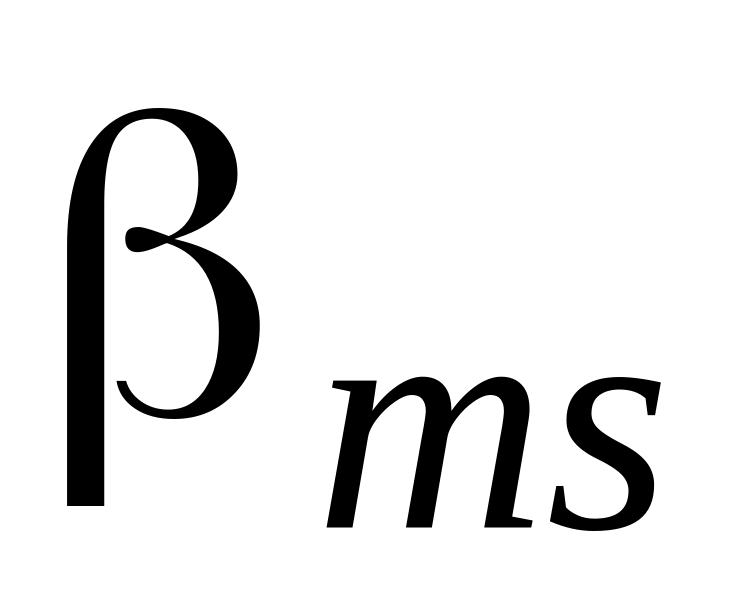
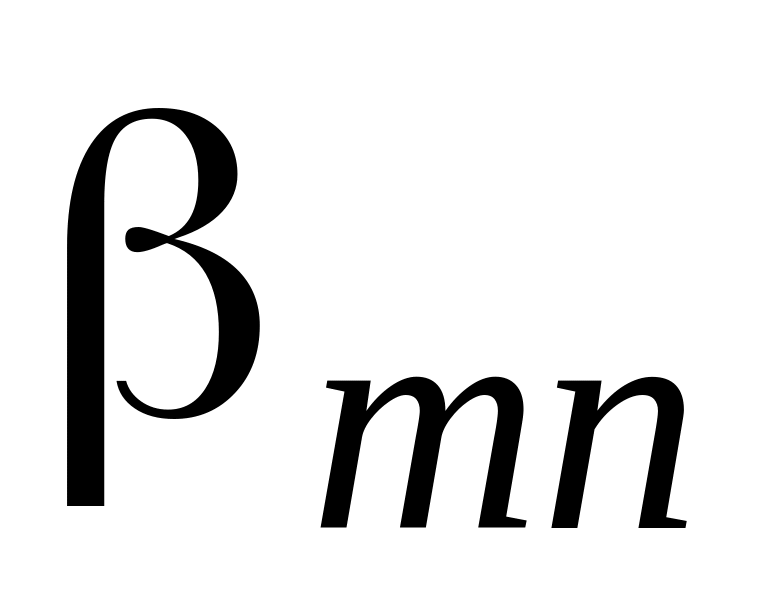
где для удобства обозначений положено

, , .

Один шаг МЖИ с разрешающим элементом означает переход к новой таблице:

		...		...
		...		...
...	.	.	.	.	.
		...		...
...	.	.	.	.	.
		...		...

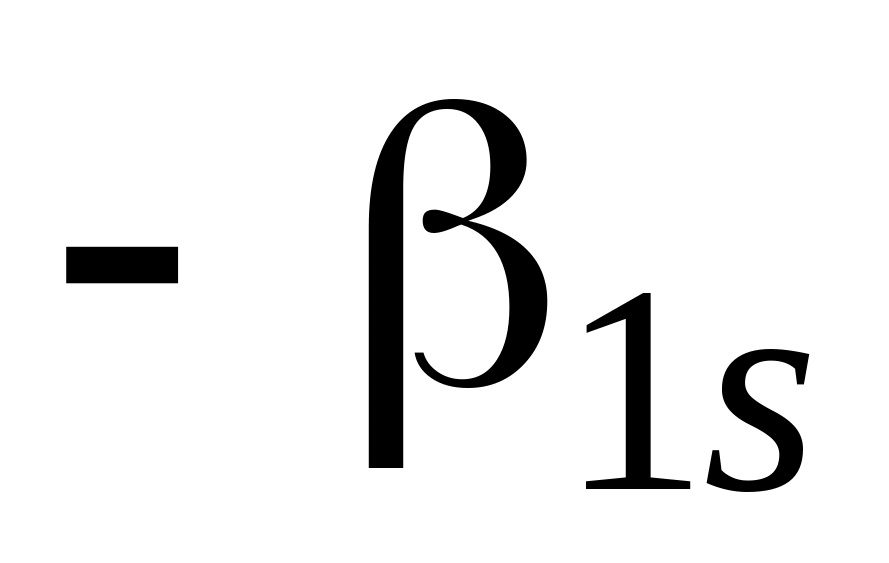
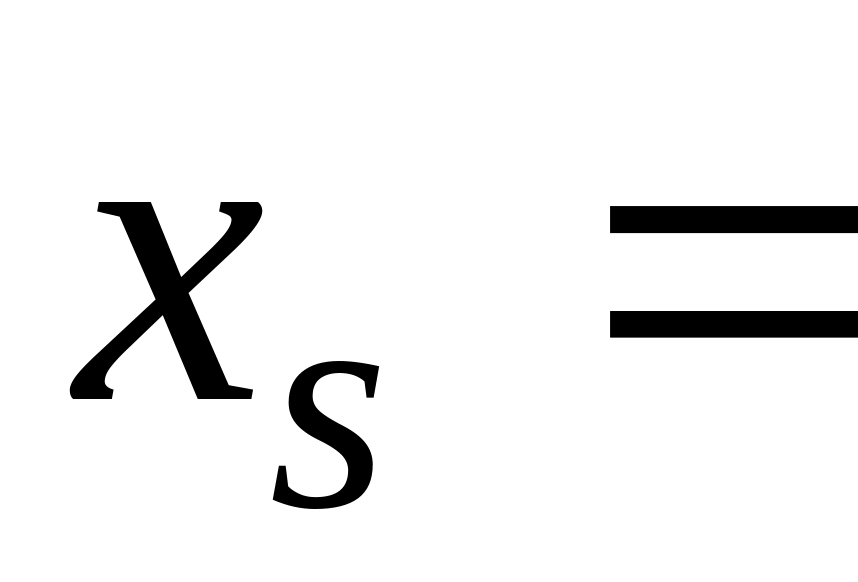
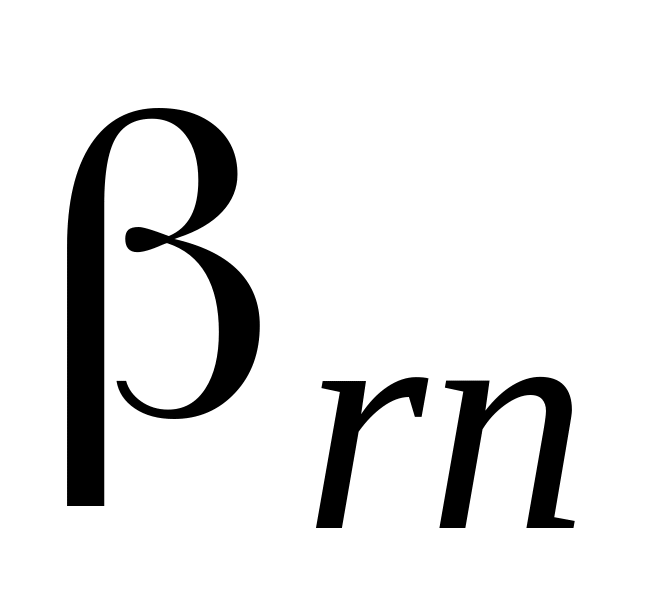
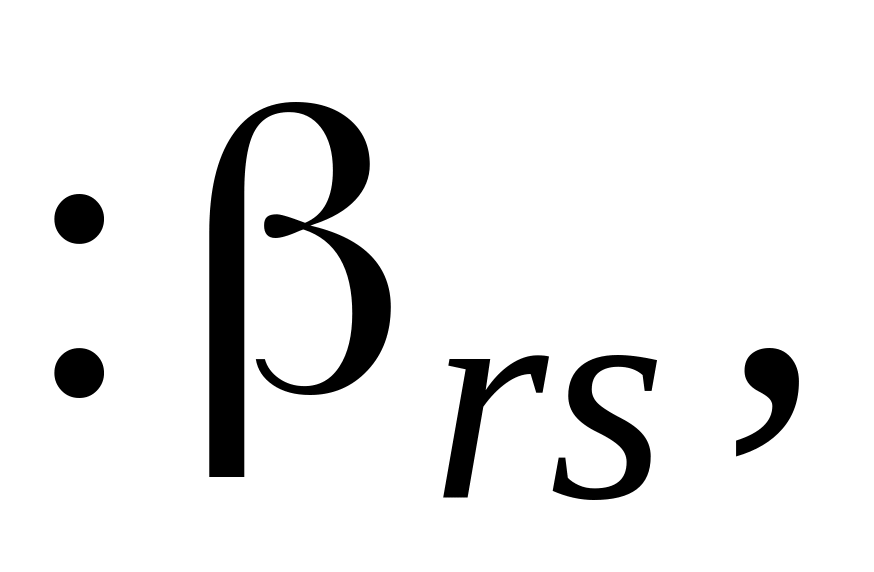
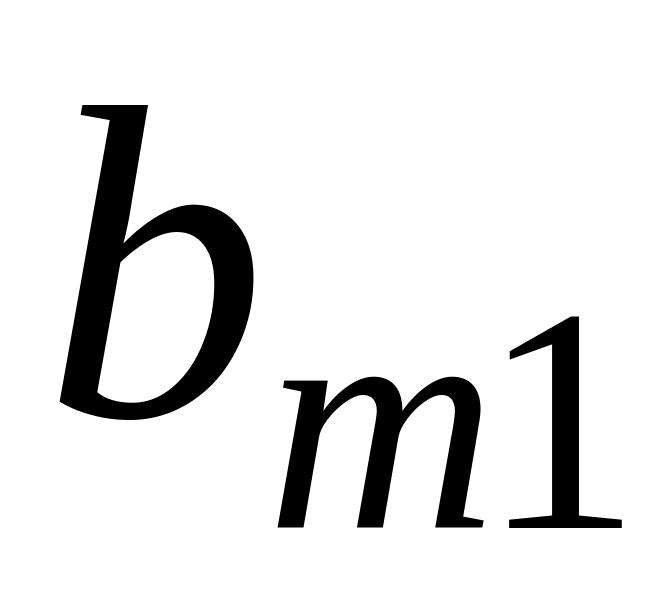
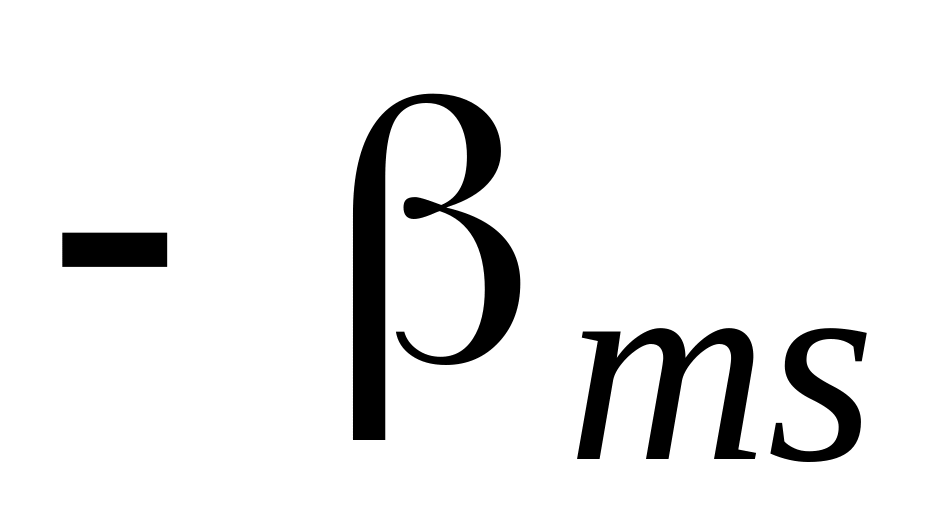
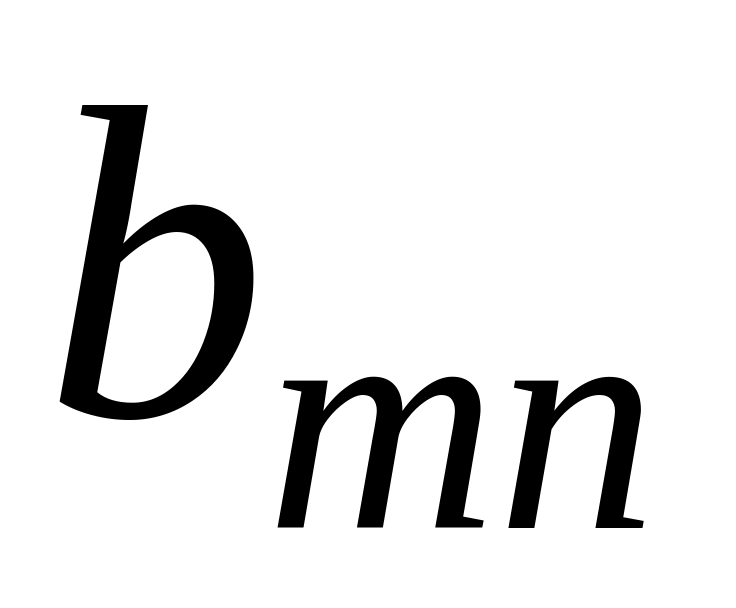
которая получается из предыдущей по правилам 1-5 ОЖИ, с тем лишь исключением, что правила 2 и 3 меняются ролями, а именно:

2. Остальные (кроме разрешающего) элементы разрешающей строки (r-й) остаются без изменений.

3. Остальные элементы разрешающего столбца (s­го) меняют лишь свои знаки.

Примечание. Соответственно изменяются правила 2 и 3 алгоритма, ориентированного на машинную реализацию (см. п. 1.1).

Изложим далее алгоритм решения основной задачи линейного программирования с помощью симплекс-метода.