2.3. Решение игровой задачи путем сведения ее к паре взаимно-двойственных задач линейного программирования

При составлении платежной матрицы Q вычисляем ее элементы по формуле (2.2.2) и берем их с обратным знаком, при этом получим все диагональные элементы, равные нулю, т.е. матрица Q будет иметь вид

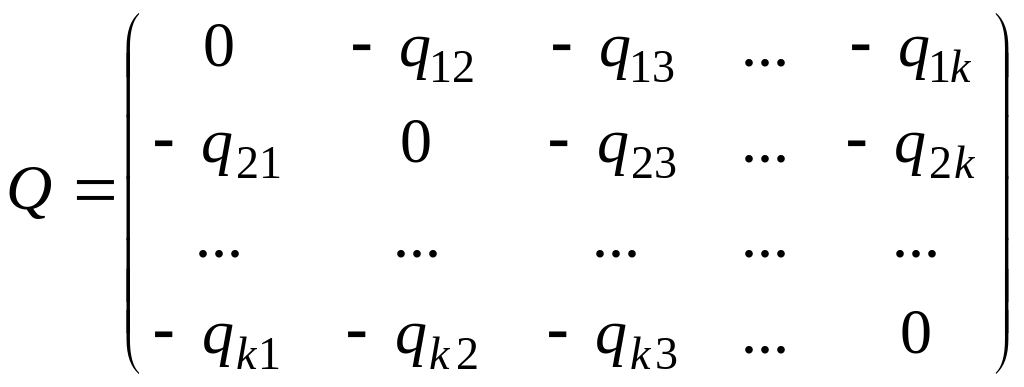(2.3.1)

В платежной матрице (2.3.1) все элементы, кроме диагональных, меньше нуля, что не позволяет использовать симплекс-метод для нахождения оптимального решения после сведения матричной игры к задаче линейного программирования. Поэтому предварительно матрицу Q (2.3.1) заменим эквивалентной ей матрицей с неотрицательными элементами, для чего к каждому элементу матрицы (2.3.1) прибавим одно и то же число, равное , т.е. число, равное максимальному по модулю элементу матрицы (2.3.1). В результате получаем матрицу с неотрицательными элементами:

, (2.3.2)

в которой диагональные элементы равны и имеют максимальное значение и ij. Такая замена не изменит решения игры, изменится только ее цена (см. доказательство теоремы фон Неймана). Эквивалентная этой игре пара двойственных задач линейного программирования может быть представлена в совмещенной таблице вида

		v1=	v2=	…	vk=	W=
		-	-	…	-	1
u1	=			…		1
u2	=			…		1	(2.3.3)
…	…	.	.	.	.	.
uk	=			…		1
1	Z =	-1	-1	…	-1	0

Решив с помощью симплекс-метода пару двойственных задач, представленных таблицей (2.3.3), получим max Z = min W, которые будут достигаться при каких-то определенных значениях . Оптимальную смешанную стратегию первого игрока можно определить из полученных оптимальных решений данной пары двойственных задач по формуле

. (2.3.4)

При этом удовлетворяет условию .

Таким образом, искомый наилучший компромиссный вектор входных сигналов относительно заданных критериев оптимальности представляет собой выпуклую линейную комбинацию из оптимальных векторов входных параметров и имеет вид:

. (2.3.5)

Контрольні запитання

1. Задачи многокритериальной оптимизации

2. Критерий выбора компромиссного решения.

3. Игровой подход.

4. Сведение игровой задачи к паре двойственных задач.

Рекомендована література: [9, 10, 13]

Тема 7.

Чєбишевська точка системи лінійних рівнянь та нерівностей

Розглянуті питання з теми:

Чєбишевське наближення несумісної системи. лінійних рівнянь. Приєднана задача лінійного програмування. Чєбишевська точка системи лінійних нерівностей.

Для решения задачи чебышевского приближения несовместной системы

(6.1.1)

можно осуществить переход к присоединенной задаче линейного программирования, заключающейся в минимизации линейной формы

(6.1.2)

при ограничениях , , которые после раскрытия модулей перепишутся в виде

(6.1.3)

.

Симплекс-таблица присоединенной задачи линейного программирования имеет следующий вид

		...			1
		...		-1
...	...	...	...	...	...
		...		-1
		...		-1		(6.1.4)
...	...	...	...	...	...
		...		-1
Z=	0	...	0	-1	0

С помощью последовательных шагов МЖИ из таблицы исключаются свободные переменные и несвободная переменная (т.к. ), выражения для них выписываются отдельно. Далее применяется алгоритм симплекс-метода для отыскания опорного решения и минимизации Z(x).

После получения решения задачи минимизации вычисляются координаты чебышевской точки . Уклонение L равно полученному значению Z. Очевидно, что (n+1) уклонение среди вычисленных уклонений должны быть по модулю равны L, а модули остальных  L.