Контрольні запитання

1. Задачи исследования операций.

2. Проблема “Двух картошек”

3. Обыкновенные жордановы исключения.

4. Геометрическая интерпретация.

5. Применение жордановых исключений в линейной алгебре

6. Модифицированные жордановы исключения.

7. Основная задача линейного программирования

Рекомендована література: [1,3,8,9,10]

Тема 2.

Геометрична інтерпретація та метод рішення основної задачі лінійного програмування

Розглянуті питання з теми:

Опуклість. Теореми 1, 2, 3. Геометрична інтерпретація. Теорема 4. Метод рішення. Відшукання опорного рішення. Правило вибору розрішного елемента і його обґрунтування. Боротьба з зацикленням. Пошук оптимального рішення. Рішення задачі мінімізації. Монотонність і кінцевість симплекс-методу.

Л3.3. Свойства допустимой области

Выпуклой линейной комбинацией точек -мерного евклидова пространства называется точка

, (3.3)

где . Здесь , .

Если , то множество точек (3.3) называют отрезком, соединяющим точки и . Любую точку этого отрезка можно представить как .

Множество называется выпуклым, если вместе с любыми двумя своими точками оно содержит и соединяющий их отрезок.

Теорема 3.1. Пусть множество выпукло. Тогда выпуклая комбинация произвольного количества точек этого множества принадлежит этому множеству.

Д о к а з а т е л ь с т в о. Пусть . Покажем, что .

Доказательство проведем методом математической индукции. Для теорема очевидна. Для теорема справедлива по определению выпуклого множества.

Предположим, что теорема справедлива для , т.е.

. (3.4)

Докажем, что теорема верна и для , т.е.

. (3.5)

Можно предположить, что в (3.5) , так как в противном случае теорема верна по предположению. Поскольку , то .

Обозначая , имеем. Теперь

.

Поскольку в силу (3.4), по условию, то по определению выпуклого множества , что и требовалось доказать.

Пересечением двух множеств и называется такое множество , которое состоит из точек, принадлежащих одновременно как , так и .

Полупространством в называется множество точек , удовлетворяющих соотношению

, (3.6)

где - некоторые константы.

Гиперплоскостью называется множество точек , удовлетворяющих линейному уравнению

. (3.7)

Любая гиперплоскость (3.7) может быть представлена как пересечение двух полупространств

, .

Многогранным множеством называется пересечение конечного числа полупространств. Ограниченное многогранное множество называется многогранником.

Каждое из неравенств системы (3.2) определяет полупространство. Соответственно, допустимое множество , определяемое системой (3.2), является (если оно не пусто) многогранным множеством.

Покажем, что многогранное множество  выпукло.

Теорема 3.2. Полупространство является выпуклым множеством.

Д о к а з а т е л ь с т в о. Пусть - две точки полупространства (3.6), т.е.

, (3.8)

Покажем, что точка , также принадлежит полупространству, т.е. удовлетворяет (3.6). Действительно, в силу (3.8) получаем

Теорема доказана.

Теорема 3.3. Пересечение двух или более выпуклых множеств является выпуклым.

Д о к а з а т е л ь с т в о. Пусть . По определению пересечения и . Так как и выпуклы, то и , где .

Следовательно, , что и требовалось доказать.

Следствие. Гиперплоскость является выпуклым множеством.

Из приведенных определений и доказанных теорем вытекает следующее утверждение.

Многогранное множество, если оно не пустое, является выпуклым.

Л3.4. Геометрическая интерпретация ОЗЛП

Для каждой точки значение функции можно рассматривать как уклонение точки от плоскости , которое пропорционально расстоянию этой точки от этой плоскости.

Таким образом, геометрический смысл решения ОЗЛП заключается в отыскании точки многогранного множества , которая наиболее (наименее) уклонена от плоскости .

Теорема 3.4. Пусть допустимое множество  задачи линейного программирования является многогранником. Тогда функция цели (3.1) имеет экстремальное значение в вершине .

Д о к а з а т е л ь с т в о. Нетрудно показать, что любая точка многогранника является выпуклой комбинацией его вершин. Тогда и точка , в которой функция достигает экстремума (пусть, например, минимума) представима в виде

, ,

где - вершины многогранника .

В силу линейности имеем

, (3.9)

где .

Проиллюстрируем справедливость правой части (3.9) на примере двух точек:

.

Но, по предположению, - оптимальное решение, следовательно , т.е. существует вершина , в которой линейная форма принимает минимальное значение.

Для максимума доказательство аналогично.

Рассмотрим геометрическую интерпретацию для двумерного пространства. Здесь многогранник  является многоугольником, гиперплоскости - прямыми, а полупространства - полуплоскостями (на рисунках их будем определять штриховкой в сторону выполнения неравенств). Ясно, что решением ОЗЛП будет какая-то вершина многоугольника . На Рис. 3.1а решение задачи максимизации формы дает вершина Р1, а задачи минимизации - вершина Р2, причем эти решения единственны. Случай существования бесчисленного множества решений иллюстрирует Рис. 3.1b. Случай неограниченности функции Z на  показан на Рис. 3.1c, случай отсутствия решения - Рис. 3.1d (многогранник решений - пустое множество, система ограничений несовместна).

Рис. 3.1.

Лекция 4. Симплекс-метод решения ОЗЛП

Основным методом решения задач линейного программирования является так называемый симплекс-метод, основоположником которого является американский ученый Дж. Данциг.

Симплекс-метод состоит из алгоритма отыскания опорного решения системы линейных неравенств (3.2), т.е. определения координат любой вершины многогранника  (или установления факта несовместности системы), и алгоритма направленного перехода от полученного опорного решения к оптимальному - вершине с максимальным (минимальным) значением функции цели (3.1). Основу вычислительной схемы симплекс-метода составляют МЖИ.

Л4.1. Переход к таблице

Функцию цели (3.1) и условия (3.2) записываются в виде следующей таблицы:

		...		...		1
		...		...
...	.	.	.	.	.	...
		...		...
...	.	.	.	.	.	...
		...		...
		...		...		0

(4.1)

Если среди ограничений (3.2) встречаются ограничения лишь на знак переменной, т.е. , то их не включают в таблицу (4.1). Если , то в системе (3.1)-(3.2) делается замена переменных , и ограничение также в таблицу не включается.

Переменные, на знак которых наложено ограничение, называются несвободными, остальные - свободными.

Верхние переменные таблицы называются базисными, левые - зависимыми. Последний столбец будем называть столбцом свободных членов, нижнюю строку - Z-строкой. Каждой таблице вида (4.1) геометрически будет соответствовать точка таблицы - начало координат пространства, определяемого базисными переменными.

Л4.2. Исключение свободных переменных

Для простоты изложения будем считать, что все переменные свободны и что ранг матрицы коэффициентов системы (3.2) равен . Тогда (см. Л2.3.) с помощью МЖИ можно перевести из верхней строки таблицы в ее левый столбец и на их место поставить соответствующие . При этом в классической постановке метода никаких ограничений на выбор разрешающих элементов не налагается, лишь бы они были отличны от нуля.

Для удобства записи можно считать, что на верх таблицы перешли , так что получена таблица вида:

		...		...		1
		...		...
...	.	.	.	.	.	...
		...		...
		...		...
...	.	.	.	.	.	...
		...		...
...	.	.	.	.	.	...
		...		...
		...		...

Выражения для переменных

выписываются из таблицы отдельно ( они понадобятся лишь после получения решения, чтобы выразить его в старом базисе).

		...		...		1
		...		...
...	.	.	.	.	.	...
		...		...
...	.	.	.	.	.	...
		...		...
		...		...

Далее продолжаем работать с оставшейся частью таблицы:

. (4.2)

Так как по условию (3.2) то переходим к следующей обычной формулировке ЛП-задачи (например максимизации):

Дана линейная функция

(4.3)

и задана система неравенств (ограничений)

, (4.4)

причем .

Из всех неотрицательных решений системы (4.4) найти такое, которое максимизирует линейную функцию (4.3).

Замечание. Подчеркнем что исключению подлежат лишь свободные переменные. Несвободные же переменные (которые, как указано выше, можно считать неотрицательными не исключают. Таким образом, если, как обычно, , то после п. Л4.1 приступают сразу к п. Л4.3.

Л4.3. Нахождение опорного решения

Если в таблице (4.2) все элементы столбца свободных членов неотрицательны ( ), то точка таблицы (с координатами ) является опорным решением, так как для нее , и, следовательно, все , и система (3.2) удовлетворяется.

Если же в таблице (4.2) хотя бы один свободный член отрицателен (например, - й, где ), то в точке таблицы и ,следовательно, она не является решением систем (4.4) и (3.2).

Переход от текущей таблицы к следующей, содержащей меньшее (в общем случае - не большее) число отрицательных свободных членов, осуществляется посредством МЖИ с разрешающим элементом, выбор которого производится по следующему правилу.

1) Находим строку (первую попавшуюся) с отрицательным элементом столбца свободных членов (если таковой не оказалось, то опорное решение уже найдено, и следует переходить к поиску оптимального решения). Пусть, например, ;

2) среди коэффициентов этой строки находим первый попавшийся отрицательный ( если такового не оказалось, то система ограничений ЛП-задачи противоречва). Пусть, например, , т.е. s-й столбец - разрешающий;

3) для выбора разрешающей строки находим минимальное неотрицательное среди отношений элементов столбца свободных членов к соответствующим отличным от нуля коэффициентам разрешающего столбца (назовем его МНО). Пусть МНО достигается при , т.е.

.

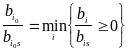Тогда -ю строку берем в качестве разрешающей, так что - разрешающий элемент.

Примечание. Если часть свободных членов равна нулю, то говорят что имеет место вырождение. При этом МНО 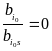. Коэффициент следует брать в качестве разрешающего лишь при , в противном случае ищем новое МНО, не учитывая -ю строку.

Нетрудно убедиться, что такой выбор разрешающего элемента гарантирует, что количество отрицательных свободных членов не увеличится.

Действительно, после МЖИ

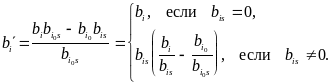
Т.е. всегда при .

Если разрешающим оказался , то после шага МЖИ новый свободный член станет положительным.

Если же разрешающий элемент не попал в r-ю строку, то новый останется еще отрицательным, но уменьшится по модулю. В этом случае продолжаем работать с r-й строкой (делать МЖИ, выбирая разрешающий элемент по изложенному правилу), и либо станет неотрицательным, либо установим несовместность системы ограничений.

Повторяем п.п. 1-3, и после конечного (но заранее неизвестного) количества шагов МЖИ либо установим несовместность системы ограничений, либо получим таблицу с неотрицательным столбцом свободных членов. Точка этой таблицы и будет соответствовать опорному решению (при вырождении не исключена возможность так называемого зацикливания (См. Л7)).

Лекция 5. Симплекс-метод решения ОЗЛП (продолжение)

Л5.1. Обоснование правила выбора разрешающего элемента при поиске опорного решения

Пусть все свободные члены таблицы (4.2) отличны от нуля (нет вырождения).

Если опорное решение найдено ( ) то точка таблицы ( точка P₀ с координатами ) является вершиной многогранника . Если же хотя бы один из свободных членов отрицателен (например, ), то P₀ и область  находятся в разных полупространствах относительно плоскости .

Действительно,

,

в то время как для точек многогранника  обязательно .

Проинтерпретируем правило выбора в двумерном пространстве (см. Рис. 5.1), т.е. для последней таблицы базисными переменными являются и .

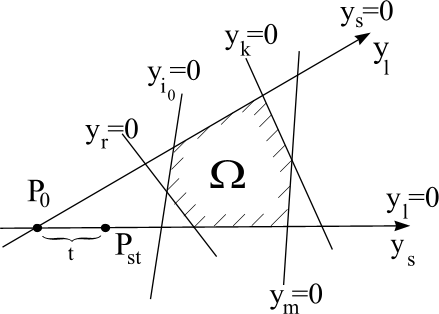
Рис. 5.1.

Так как , то двигаться к опорному решению следует в направлении к отделяющей прямой , например, вдоль . Обозначим через точку на оси с координатами

.

При движении к  модуль уклонения от отделяющей плоскости должен уменьшаться:

,

т.е.

.

Так как , то последнее неравенство означает, что

,

т.е. и, в силу положительности t, что . Таким образом установлено, что по оси следует двигаться тогда и только тогда, когда s-й столбец содержит отрицательный коэффициент r-й строки.

Если в r-й строке нет отрицательных коэффициентов, то движение к отделяющей плоскости невозможно ни по одной из осей и это является признаком несовместности (противоречивости) системы ограничений, т.е. многогранник  пустой. В этом случае , и неотрицательность несовместима с требованием неотрицательности .

Двигаться по оси следует до встречи с отделяющей плоскостью (не обязательно с ).

Каждый шаг МЖИ с разрешающим элементом, выбранным из s-го столбца, как раз и приводит к переносу точки таблицы в одну из точек пересечения плоскостей системы ограничений в направлении (на рисунке таких точек четыре).

Алгоритм симплекс-метода предлагает двигаться из точки таблицы по оси лишь до первой встречи с новой плоскостью (в нашем случае это плоскость ). Такой выбор исключает возможность «перепрыгивания» через , обеспечивает монотонное но не обязательно оптимальное (по количеству МЖИ) приближения к .

При движении из P₀ в направлении можно встретить плоскости

,

для которых . Очевидно, первой встретится плоскость для которой . Такое отношение здесь обязательно найдется, так как . После шага МЖИ с разрешающим элементом точка таблицы переместится в начало новой системы координат, полученной заменой базисной плоскости на новую .

Если МНО получилось при (что желательно), то в результате шага МЖИ перейдем к точке, которую отделяет от  меньшее, чем предыдущую, число плоскостей (количество отрицательных свободных членов в таблице уменьшится).

Если же МНО получилось при , то в результате шага МЖИ количество отрицательных свободных членов в таблице не изменится, однако при этом уменьшится , т.е. точка таблицы приблизится к отделяющей плоскости .

Если имеет место вырождение (часть свободных членов равна нулю), то через точку таблицы проходит больше чем плоскостей. Тогда МНО=0, и в результате шага МЖИ с разрешающим элементом точка таблицы останется на прежнем месте (т.к. ), но базисная плоскость заменится плоскостью , в результате чего появляются новые направления движения к  (о борьбе с возможным при этом зацикливанием см. Л7). Таким образом, после конечного количества шагов мы либо выйдем из вырожденной вершины, либо обнаружим противоречивость системы ограничений.

5.2. Поиск оптимального решения (решение задачи максимизации)

Пусть рассматривается задача максимизации линейной формы

при ограничениях

,

и пусть после исключения свободных переменных и отыскания опорного решения получена таблица

		...		...		1
		...		...
...	.	.	.	.	.	...
		...		...
...	.	.	.	.	.	...
		...		...
		...		...

,

так что .

В зависимости от знаков коэффициентов Z-строки возможны два случая.

1. Все коэффициенты Z-строки неотрицательны.

Если , то задача линейного программирования решена, причем и достигается в точке . Действительно, в этой точке имеем , т.е. удовлетворяются ограничения (3.2), и так как в любой другой точке многогранника  все неотрицательны, то , т.е. - максимальное значение .

2. Среди коэффициентов Z-строки есть отрицательные.

Пусть . В этом случае нельзя утверждать, что значение функции в точке P₀ с координатами является максимальным. Действительно, если в направлении от P₀ взять точку P_s с координатами ( ), принадлежащую  (т.е. ), то в этой точке .

Чтобы осуществить переход от точки P₀ к соседней вершине многогранника  с большим (не меньшим) значением , необходимо произвести шаг МЖИ с разрешающим элементом, выбранным по следующему правилу.

1) Находим столбец (первый попавшийся) с отрицательным коэффициентом Z-строки (если таковых не окажется, то задача уже решена). Пусть, например, т.е. s-й столбец - разрешающий;

2) для выбора разрешающей строки находим МНО, используя процедуру выполнения п. 3 правила выбора разрешающего элемента при поиске опорного решения (при поиске оптимального решения, в отличие от поиска опорного, МНО может не существовать, если в s-м столбце не оказалось положительных элементов — это означает неограниченность сверху функции цели ). Пусть МНО достигается при , т.е.

.

Тогда -ю строку берем в качестве разрешающей, так что - разрешающий элемент.

Примечание. Если МНО 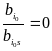, то коэффициент можно брать в качестве разрешающего лишь при , в противном случае ищем новое МНО, не учитывая -ю строку.

Поясним случай неограниченности функции цели. Действительно, если , а в s-м столбце нет положительных элементов, то для любого точка с координатами ( ) будет принадлежать , так как в этом случае , а соответствующее значение функции можно сделать сколь угодно большим при неограниченном увеличении .

После шага МЖИ с разрешающим элементом коэффициент станет положительным (при этом возможно появление новых отрицательных коэффициентов в Z-строке).

Если все новые коэффициенты Z-строки неотрицательны то задача решена.

Л5.3. Обоснование правила выбора разрешающего элемента

Пусть среди коэффициентов Z-строки есть отрицательные и, следовательно, нет уверенности в том, что точка P₀ с координатами дает максимум функции . Переход к соседней вершине означает движение из P₀ по ребру многогранника вдоль некоторой оси , выбранной так, чтобы в точке с координатами ( ) значение было больше, чем в P₀. Т.е. . Отсюда и .

Таким образом, для увеличения следует двигаться по ребру многогранника вдоль базисной оси, определяемой столбцом таблицы, содержащим отрицательный коэффициент в Z-строке.

Пусть . Ясно, что по выбранному ребру можно двигаться лишь до соседней вершины многогранника ( чтобы не сойти с  !), т.е. до встречи с некоторой плоскостью , где . В точке встречи с этой плоскостью, если , получим , следовательно , и так как , то . Первой, очевидно, встретится плоскость для которой .

В случае вырождения, т.е. когда среди свободных членов встречаются равные нулю, искомая «соседняя» вершина может совпасть с исходной P₀ ( движения не будет). Можно избежать таких «пустых» МЖИ, выбирая среди столбцов с отрицательными элементами Z-строки в качестве разрешающего тот столбец (если таковой существует), у которого против всех нулевых свободных членов нет положительных коэффициентов.

После конечного числа шагов мы либо сойдем с рассматриваемой вершины, либо убедимся, что в этой вершине достигается искомый максимум, либо обнаружим неограниченность функции Z (о борьбе с возможным при этом зацикливанием см. Л7).

Лекция 6. Симплекс-метод решения ОЗЛП (продолжение)

Л6.1. Монотонность и конечность симплекс-метода

Чтобы убедиться в монотонности алгоритма симплекс-метода, достаточно показать, что значение функции Z (определяемое последним элементом Z-строки) не убывает при переходе от одного опорного решения к другому в процессе поиска оптимального решения.

Действительно, для нового значения , которое обозначим (учитывая, что ), получим

.

Таким образом, если , то , т.е. имеет место строгая монотонность рассмотренного шага. Если же , то и имеет место вырождение (о борьбе с возможным при этом зацикливанием см. Л7).

Конечность алгоритма симплекс-метода легко устанавливается в случае отсутствия вырождения, так как многогранник  имеет конечное число вершин, а возвращение к раз использованной вершине невозможно в силу монотонности алгоритма.