Міністерство освіти і науки України

Національний аерокосмічний університет

ім. М.Є. Жуковського

"Харківський авіаційний інститут"

Кафедра 603

Конспект лекцій

“Методи оптимізації та дослiдження операцiй”

за фахом «Програмна інженерія»

факультету №9

Харків – 2011

Поиск оптимального значения функции с помощью метода наискорейшего спуска

Применение метода наискорейшего спуска для решения задачи минимизации без ограничений было рассмотрено еще известным французским математиком Коши. Как известно из курса математического анализа, градиент целевой функции в любой точке x=(x₁,…,x_n) есть вектор в направлении локального увеличения . Следовательно, для минимизации целевой функции нужно двигаться в направлении, противоположном градиенту , т.е. в направлении наискорейшего спуска, поскольку отрицательный градиент в точке =(x₁^(k),…,x_n^(k)) направлен в сторону наибольшего уменьшения по всем компонентам x и ортогонален линии уровня в точке , где k – номер шага метода, k=0, 1, …. Введение направления, противоположного градиенту, т.е. направления наискорейшего спуска, дает следующую формулу перехода из в :

(3.1.1)

Отрицательный градиент дает только направление оптимизации, но не величину шага. При этом можно использовать различные версии метода наискорейшего спуска в зависимости от процедуры выбора . Поскольку один шаг в направлении наискорейшего спуска в общем случае не приводит в точку минимума , формула (3.1.1) должна применяться несколько раз до тех пор, пока минимум не будет достигнут. В точке минимума все сотавляющие вектора градиента равны нулю, т.е. критерий останова алгоритма поиска:

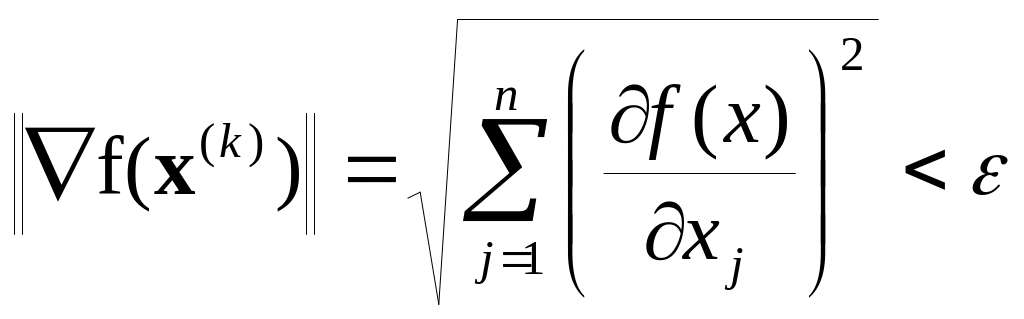(3.1.2)

Используем следующий метод нахождения . Пусть - функция от . Наращиваем от 0 с малым шагом до тех пор, пока не получим .

Построим полином второго порядка для по трем точкам (0, /2, ):

, где . (3.1.3)

Составляем систему:

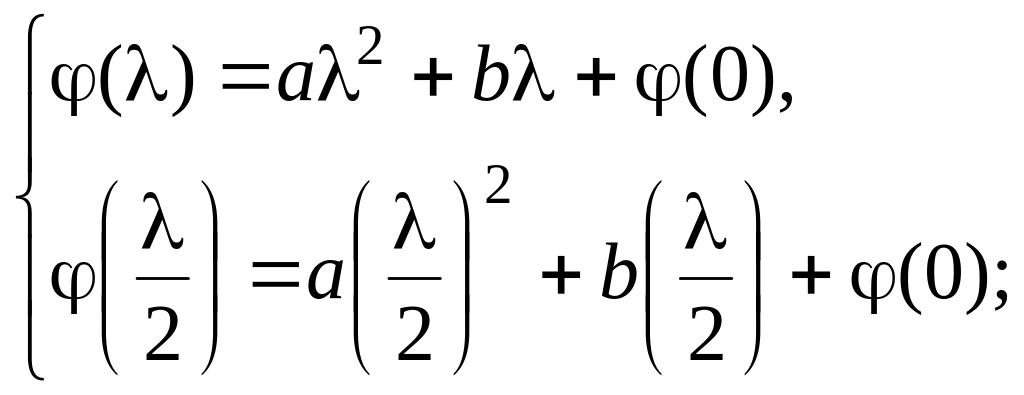(3.1.4)

решаем ее относительно коэффициентов a и b, после чего находим оптимальное значение как координату экстремума параболы по формуле:

. (3.1.5)

Для вычисления градиента функции воспользуемся определением производной , пусть , тогда

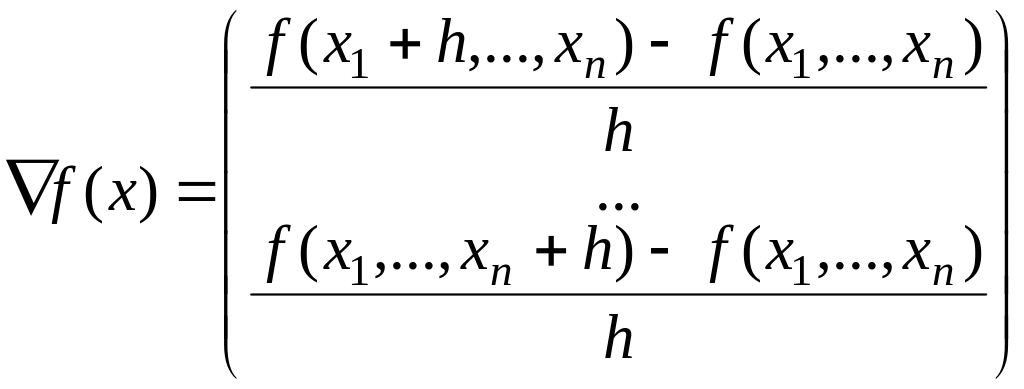(3.1.6)

Таким образом, используя формулы (3.1.1)-( 3.1.6), получаем минимизирующую последовательность и искомое значение .

Использование метода оврагов для поиска экстремумов функции

Овражная ситуация создается потому, что в практике встречается большое количество задач, в которых независимые переменные по-разному существенно влияют на поведение функции цели и потому имеет смысл по-разному строить поиск вдоль этих переменных.

Разобьем переменные функции на две группы. К первой группе отнесем переменные, незначительное варьирование которыми приводит к значительным изменениям функции цели. Частные производные для этой группы переменных велики по модулю. Будем считать, что они удовлетворяют условию

Переменные этой группы будем называть несущественными, подразумевая под этим простоту организации поиска вдоль этих переменных. К существенным переменным отнесем те, для которых

при . Организовать поиск вдоль этих переменных существенно сложно. Функцию цели (здесь ), оптимизируемые переменныe которой хорошо разбиваются на такие группы, называют хорошо организованной функцией. В противном случае функцию следует считать плохо организованной.

Например, функцию следует считать хорошо организованной, так как ее переменные четко подразделяются на две группы: несущественные и существенные переменные. В противоположность этому функция - плохо организована, потому что ее переменные не допускают четкого деления на сущесвтенные и несущественные. Как правило, хорошо организованная функция имеет «овраги». Однако, в общем случае, плохо организованная функция тоже может иметь «овраги».

При минимизации функции по методу оврагов поступаем следующим образом.

Выбираем случайным образом точки и ) (считаем, что точки находятся на склоне «оврага»);

Находим точку , расположенную близко к дну «оврага». Для этого, например, можно, взяв стартовую точку , применить одну итерацию алгоритма, описанного в лабораторной работе №1.

Аналогично, взяв стартовую точку , находим точку , также расположенную на дне «оврага».

Далее предполагается, что – в противном случае стартовые точки и следует поменять местами.

Вычисляем

Точка находится на склоне «оврага»,

.

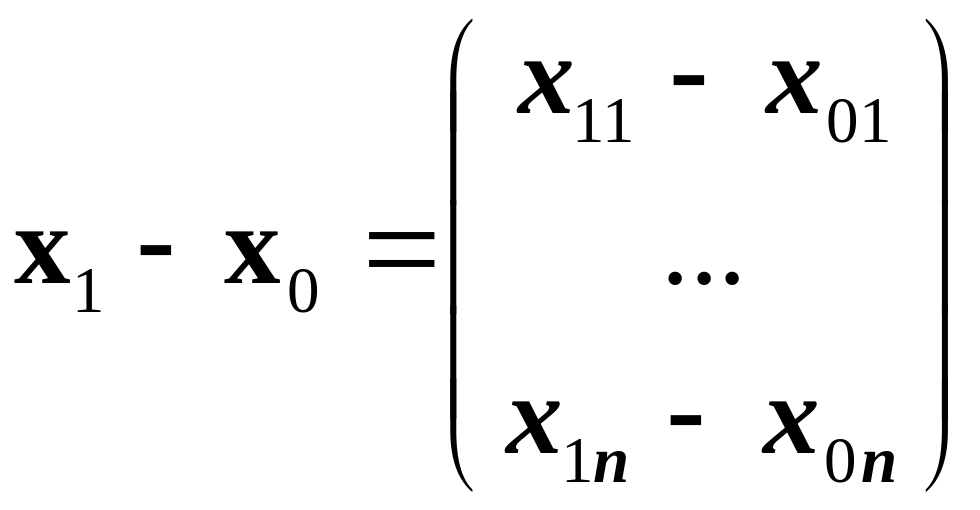
К величине «овражного» шага предъявляются следующие требования:

1. чем круче поворот, тем меньше шаг;

2. чем прямолинейнее дно, тем больше должен быть шаг;

3. в любом случае следует придерживаться дна «оврага».

Таким образом, формула нахождения следующей точки на склоне «оврага» выглядит следующим образом:

,

где согласно стратегии Гельфанда-Цетлина: , С>1, - угол между векторами и , С – параметр чувствительности к кривизне дна «оврага»;

,

где - скалярное произведение векторов и ;

- произведение по модулю векторов и .

В формуле для h_k+1 распишем h_k через h_k-1 (по той же формуле), h_k-1 через h_k-2, и т.д_.:

.

Пусть . Таким образом, .

выбирают произвольно. Например, = .

Если в процессе поиска возникнет ситуация , то следует начать поиск из точки с меньшим шагом.

Останов в овражной ситуации выполняется при .