Задача 1м, 1т (4 бали)

З’ясувати, чи для кожного натурального числа існує квадратна матриця порядку , визначник якої дорівнює 1, а всі елементи – цілі числа, кожне з яких не меньше за .

Відповідь: так, існує.

Розв’язання.

Матрицю з вказаними властивостями можна отримати, наприклад, з одиничної матриці порядку , визначник якої дорівнює 1, за допомогою елементарних перетворень, що не змінюють визначник матриці:

Задача 2м, 2т (4 бали)

Нехай і – деякі точки простору. Відомо, що . Знайти скалярний добуток .

Відповідь:

Розв’язання.

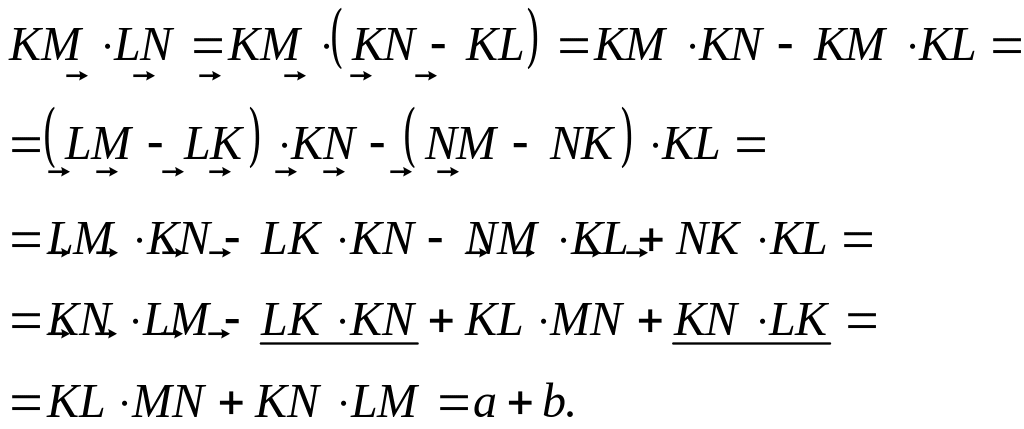
Задача 3м (7балів)

На площині прямокутних декартових координат знайти множину точок, із кожної з яких можна провести рівно три нормалі до параболи .

Відповідь: .

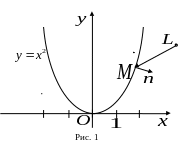
Розв’язання.

Нехай – довільна точка площини, а – довільна точка параболи (рис.1). За вектор нормалі до параболи у точці можна взяти вектор . Вектор також є вектором нормалі до параболи у точці тоді і тільки тоді, коли вектори і колінеарні, тобто коли виконується рівність або . (1)

Підставляючи у рівняння (1), після перетворень дістаємо

. (2)

Таким чином, треба знайти множину точок , для яких рівняння (2) має рівно три різних дійсних кореня.

Якщо , то рівняння (2) має три різних дійсних кореня при і один дійсний корінь при (при дійсний корінь є кратним).

Нехай .

Розглянемо функцію . Обчислимо похідну цієї функції:

Якщо , то за винятком при . Тому функція є строго зростаючою на всій числовій вісі, і оскільки , то при і довільному рівняння (2) має один дійсний корінь.

Якщо , то похідна має два дійсних різних кореня:

и .

У точці функція має мінімум, причому .

У точці функція має максімум: .

Звідси випливає, що рівняння (2) має три різних дійсних кореня тоді і тільки тоді, коли виконується умова

, тобто , або .

Якщо , тобто , або , то рівняння має єдиний дійсний корінь, а якщо , тобто , або , то рівняння має два різних дійсних кореня.

Оскільки парабола симетрична відносно осі , то у випадку, коли можна зробити такі ж самі висновки, як і у випадку, коли .

Таким чином, з точки до параболи можна провести:

1) рівно три нормалі тоді і тільки тоді, коли координати цієї точки задовольняють нерівність

, ;

2) рівно дві нормалі тоді і тільки тоді, коли координати цієї точки задовольняють рівняння

, .

3) рівно одну нормаль тоді і тільки тоді, коли координати цієї точки задовольняють умовам

, або (рис.2).

Задача 3т (7 балів)

На площині прямокутних декартових координат знайти множину точок, із кожної з яких можна провести рівно дві нормалі до параболи .

Відповідь: . Див. розв’язання задачі 3М.

Задача 4м (5 балів)

Розв’язати у комплексних числах систему рівнянь:

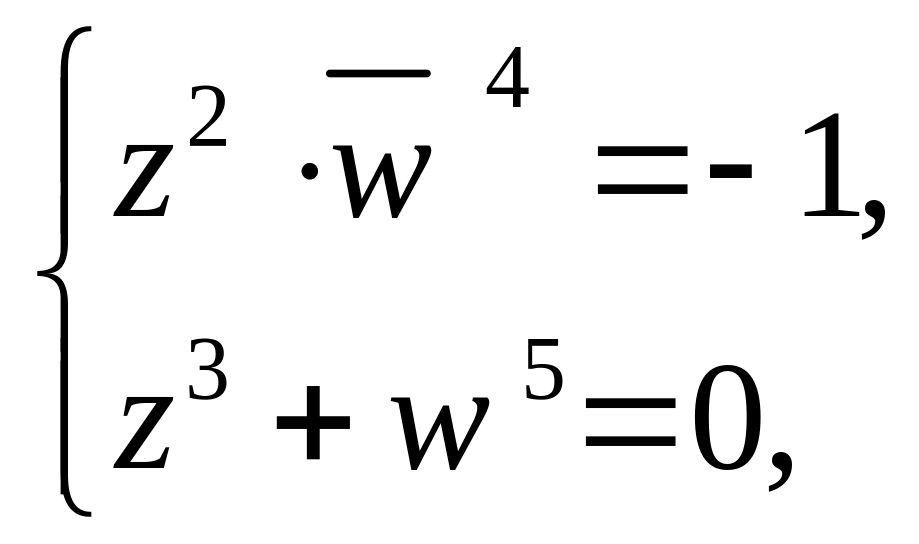
де – число, комплексно спряжене до числа .

Відповідь: ; .

Розв’язання.

Оскільки , то дана система рівнянь рівносильна системі:

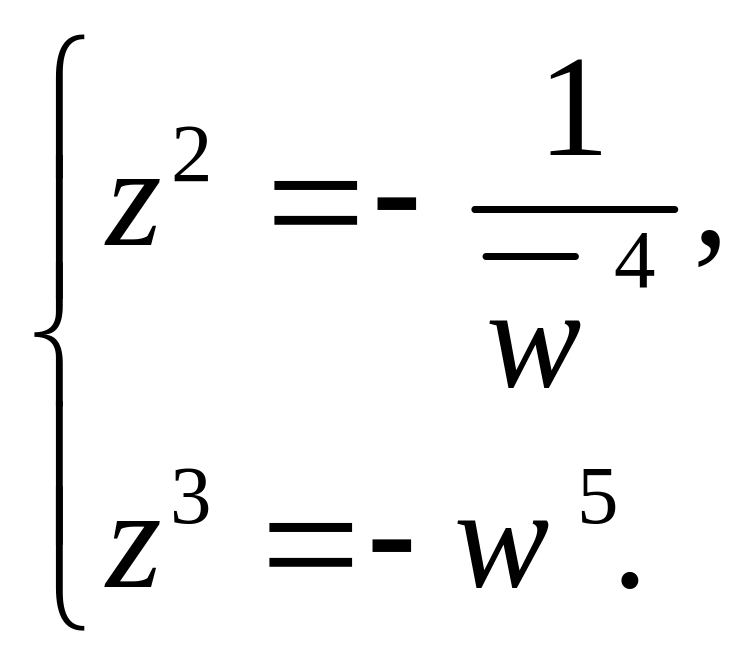
Піднесемо обидві частини першого рівняння до куба, а обидві частини другого рівняння – до квадрата. Тоді з отриманих рівнянь випливає, що

.

Звідси , або

. (1)

З рівняння (1) випливає, що , або . Тому рівняння (1) набуває вигляду або , тобто .

Таким чином, якщо пара комплексних чисел є розв’язком даної системи, то .

Нехай . Тоді вихідна система рівнянь набуває вигляду:

.

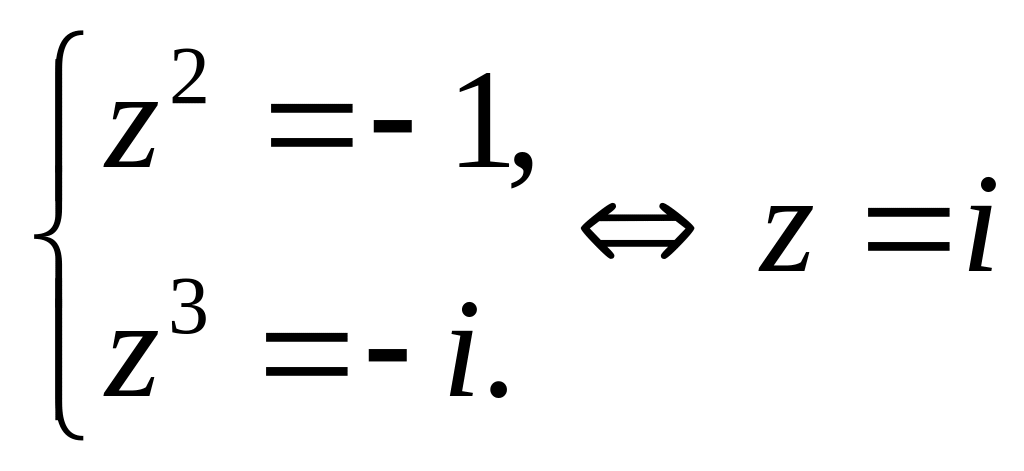Отже, впорядкована пара є розв’язком даної системи.

Якщо , то вихідна система набуває вигляду:

.

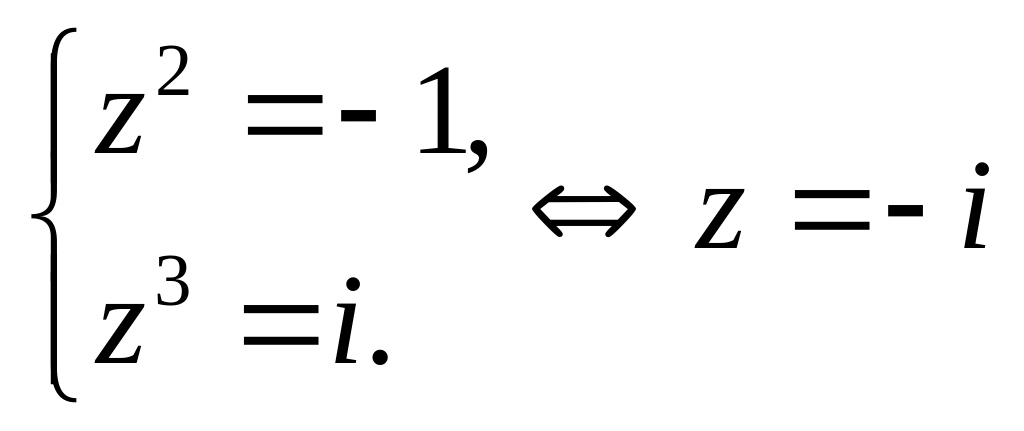Тому впорядкована пара також є розв’язком даної системи.

Таким чином, дана система має два розв’язки: и .