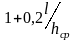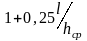8.4 Методы расчета среднего удельного давления при прокатке толстых полос и профилей непрямоугольного сечения

Процессы прокатки толстых полос и профилей непрямоугольного поперечного сечения отличаются от процессов прокатки тонких широких полос характером напряженно-деформированного состояния металла в очаге деформации: оно является не плоским, а объемным.

Поэтому при расчете энерго-силовых параметров этих процессов нельзя пренебрегать уширением, неравномерностью напряжений и деформаций по толщине и ширине прокатываемых полос.

Общепризнанные аналитические методы расчета среднего удельного давления, основанные на уравнениях механики сплошной среды и математической теории пластичности, для процессов прокатки толстых полос и профилей непрямоугольного сечения отсутствуют.

В инженерной практике для указанных видов сортамента проката получили распространение приближенные методы расчета величины p_ср, подробно рассмотренные в учебном пособии Г.С Никитина [15], обобщившего в 2009 году работы А.И Целикова и его научной школы, а также известных ученых В.С. Смирнова, С.И. Губкина, М.А. Зайкова, Е.П. Унксова, П.К. Тетерина, А.П. Чекмарева, В.М. Клименко и др., выполненные в 50^х-80^х годах 20 века.

В основе этих методов лежит эмпирическое выражение:

(8.9)

где: γ – коэффициент, учитывающий влияние среднего главного нормального напряжения на объемное напряженное состояние металла в очаге деформации;

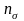- коэффициент напряженного состояния металла, учитывающий влияние трения между полосой и валками, натяжений полосы, внешних зон очага деформации;

- коэффициент, учитывающий особенности прокатки в калибрах;

- сопротивление пластической деформации металла, зависящее от марки стали, температуры прокатки, предшествующего наклепа и скорости деформации.

Ниже изложены методы определения величин, входящих в выражение (8.9), основанные на рекомендациях работы [15]. Из этих рекомендаций мы выбрали наиболее достоверные и обоснованные, исходя из опыта расчетов энергосиловых параметров различных процессов прокатки.

а) Определение коэффициента γ

: при двумерной деформации (когда уширением пренебрегают) ; при прокатке полос со свободным уширением 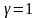. Во всех остальных случаях (при прокатке в калибрах) γ принимает промежуточное значение. В работах [1;15] рекомендуется для вычисления этого коэффициента использовать формулы М.Л. Зарощинского и В.С. Смирнова, без оценки погрешности каждой из них. Однако, поскольку формула p_срi (8.9), в которую входит γ, сама по себе является приближенной, а диапазон величин γ изменяется в пределах 15% от минимального до максимального значения, вычислять γ по какой-либо формуле не имеет смысла. Можно рекомендовать при расчетах оборудования и процессов прокатки в калибрах принимать среднее значение γ=1,075, уточняя его путем адаптации методики энерго-силового расчета на каждом стане, где представится возможность сравнить расчетные и измеренные силы прокатки.

б) Определение коэффициента

Коэффициент напряженного состояния определяют по формуле:

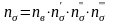(8.10)

где - коэффициенты, приближенно учитывающие влияние на среднее удельное давление ширины прокатываемого металла (n_в), трения в очаге деформации ; внешних зон очага деформации и натяжений полосы .

Для определения всех этих коэффициентов в литературе приводится большое количество эмпирических или “квазитеоретических” формул, однако данные об их достоверности и точности не приводятся. Поскольку выражения (8.9), (8.10) приближенные, не являющиеся результатом решения задачи методом механики сплошной среды или теории пластичности, уточнение входящих в них коэффициентов какими-либо теоретическими формулами не имеет смысла.

Ниже приводятся рекомендации, позволяющие определить эти коэффициенты в реальных диапазонах значений, основанные на обобщении литературных источников и на опыте расчетов энергосиловых параметров различных процессов прокатки.

Коэффициент влияния ширины полосы n_в введен в формулу (8.10) для учета особенности напряженного состояния полосы при прокатке узких полос, когда отношение <5 (где b – ширина полосы, l – длина очага деформации).

Эта особенность, обнаруженная на практике, состоит в том, что чем уже полоса, тем с меньшим сопротивлением происходит ее уширение, в результате чего контактные напряжения в очаге деформации уменьшаются.

Поэтому коэффициент n_в вводят в формулу (8.10) только при прокатке узких полос прямоугольного поперечного сечения.

Если ≥5, принимают: n_в=1. При уменьшении величина n_в уменьшается: на практике редко бывает <1…2. Минимальное значение n_в при =1: n_в≈0,8.

Исходя из этих данных, можно принимать значения n_в согласно рекомендациям таблицы 8.3

Таблица 8.3.

Приближенные значения n_в, в зависимости от отношения .

	≥5	4-5	3-4	2-3	1-2	1
nв	1	0,98	0,95	0,9	0,83	0,8

Коэффициент учитывает влияние напряжений трения на величину среднего удельного давления.

В аналитическом методе расчета величины p_ср при прокатке тонких широких полос, изложенном в п. 8.2, напряжения трения τ_x учитываются при холодной и горячей прокатке по-разному.

При холодной прокатке в очаге деформации на всей его протяженности действует закон трения скольжения τ_x=μ_ip_x, поэтому влияние трения учитывают через коэффициент трения μ_i.

При горячей прокатке преобладающую часть длины очага деформации занимает зона прилипания, в которой, вместо трения скольжения, действует закон трения покоя, поэтому для учета влияния этого вида трения следует использовать максимальное значение касательного напряжения: τ_xmax= τ_Si, где τ_Si≈0,57σ_фi – сопротивление чистому сдвигу материала полосы в i-й рабочей клети.

Исходя из этих соображений, при холодной прокатке нет необходимости рассчитывать величину p_срi и n_σ по приближенным формулам (8.9), (8.10). Если требуется определение p_срi с минимально возможными погрешностями, следует использовать формулы таблиц 8.1 и 8.2. Если устраивает приближенный результат расчета, следует рассчитывать p_срi по формуле А.И. Целикова (8.5), учитывающей и трение, и натяжение полосы (влияние внешних зон и ширины полосы при прокатке тонких широких полос отсутствует, т.е. n_в=1, =1, а коэффициент γ=1,15 входит в формулу (8.5)).

При горячей прокатке в случае двумерной деформации (когда уширение незначительно), расчет p_срi с минимальными погрешностями также следует производить по соответствующим формулам таблиц 8.1 и 8.2. Если не требуется высокой точности результата, то для расчета p_срi по приближенным формулам (8.9), (8.10) величину можно рассчитать по формулам, рекомендуемым А.И. Целиковым и Г.С. Никитиным [1; 15].

Эти формулы, скорректированные нами для случая 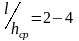(h_ср – средняя толщина полосы в очаге деформации), приведены в таблице 11.4.

Таблица 8.4

Формулы для приближенного определения коэффициента при горячей прокатке.

Значение	1-2	более 2-4	более 4
Формула

Их можно использовать и в расчетах процессов трехмерной деформации (прокатка толстых узких полос, прокатка в калибрах).

Недостаток формул таблицы 8.4 состоит в том, что они не включают величин, характеризующих трение в очаге деформации – сопротивление чистому сдвигу τ_Si и коэффициент трения μ_i, хотя предназначены для учета влияния на p_срi именно этих величин.

Тем не менее, косвенно они учитывают увеличение τ_Si по мере роста суммарного обжатия: из таблицы 8.4 видно, что с ростом отношения , происходящим по мере увеличения суммарного обжатия полосы, растет и коэффициент . Однако величина τ_Si зависит не только от суммарного обжатия, но и от свойств материала прокатываемой полосы, которые в формулах таблицы 8.4 не учитываются.

Несмотря на приближенный характер этих формул, они достоверно отражают большое влияние сопротивления деформации (главного фактора трения в зоне прилипания) на величину среднего удельного давления при горячей прокатке. Например, в первых черновых клетях двенадцатиклетевого широкополосного стана горячей прокатки (ШПСГП), где =1-2, а величина τ_xmax= τ_S(i=1,2) минимальна, по первой из формул таблицы 8.4 получим: =1+0,17(1-2)=1,17-1,34.

В последних клетях ШПСГП, где = 7-8, а величина τ_xmax= τ_S(i=11,12) максимальна, по третьей из формул таблицы 8.4 получим:

=1+0,25(7-8)=2,75-5,0.

Как видно из этого примера, рост напряжений трения в очаге деформации вызывает увеличение контактных давлений в последних клетях ШПСГП, по сравнению с первыми клетями, в 2,5-4,3 раза.

С учетом анализа, изложенного в п. 8.3, можно сделать общий вывод о влиянии напряжений на величину среднего удельного давления и силы прокатки.

Он состоит в том, что независимо от варианта процесса прокатки (горячая, холодная, с трехмерной или двумерной деформацией) и от вида трения (скольжение или прилипание, характеризуемое трением покоя), рост напряжений трения (определяемых через коэффициент трения или через сопротивление чистому сдвигу) приводит к существенному росту величин p_срi и P_i (до 5-6 раз).

Коэффициент учитывает влияние внешних зон на контактные напряжения в очаге деформации, если он характеризуется отношением <1, т.е. когда его длина меньше средней толщины полосы [1].

Такие очаги деформации имеют место в черновых клетях, толстолистовых, крупносортных, рельсобалочных станов. Для них А.И. Целиков рекомендует определять по эмпирической формуле В.В. Смирнова:

. (8.11)

График зависимости от , построенный по формуле (8.11), применимой при значениях <1, показан на рис. 8.2.

Из графика видно, что при отношениях <0,5 коэффициент может достигать величин 4-5, из-за большого подпора, создаваемого внешними зонами для металла, расположенного в высоких и коротких очагах деформации. При значениях ≥1 =1, т.е. влияние внешних зон на величины p_срi и P_i можно не учитывать.

Рис. 8.2 Зависимость от , построенная по формуле (8.11)

Коэффициент 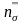, учитывающий влияние натяжений полосы, согласно рекомендации А.И. Целикова и Г.С. Никитина [1,15], можно приближенно рассчитать по формуле:

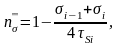(8.12)

где σ_i-1, σ_i – заднее и переднее удельные натяжения полосы в i-й рабочей клети; τ_Si≈0,57σ_фi – среднее сопротивление полосы чистому сдвигу в i-й рабочей клети.

Сопоставив выражение (8.12) с формулами (8.6), видим, что: где и - коэффициенты, учитывающие в приближенной формуле А.И. Целикова (8.5) влияние на p_срi заднего и переднего удельных натяжений.

Следовательно, физический смысл коэффициента такой же, как коэффициентов и в формуле (8.5): при отсутствии натяжений = = =1; при наличии натяжений <1, <1, <1; причем с ростом натяжений эти коэффициенты уменьшаются, вызывая уменьшение величин p_срi и P_i.

в) Определение коэффициента n_к, учитывающего особенности прокатки в калибрах.

Как отмечено выше, строгий аналитический метод определения среднего удельного давления при прокатке в калибрах, пригодный для использования в инженерных расчетах, отсутствует. Поэтому авторы работ [1; 15] предлагают рассчитывать p_срi по тем же формулам, что и для процессов прокатки на гладкой бочке, а влияние особенностей напряженного состояния металла в калибрах учитывать приближенно, вводя в формулу (8.9) дополнительный коэффициент n_к.

Для его вычисления в книге [15] предлагается несколько эмпирических формул, однако не приводится сведений об их достоверности, о погрешностях расчета величины p_срi с их использованием.

Исключение составляет эмпирическая формула В.Г. Дрозда:

(8.13)

где μ_i – коэффициент трения в очаге деформации i-й клети; l_i, Δh_i – длина очага деформации и абсолютное обжатие в i-й клети.

Относительно формулы (8.13) в работе [15] указано, что она основана на анализе большого числа экспериментальных данных и обеспечивают меньшую погрешность при расчете сил прокатки, чем другие эмпирические формулы.

Для использования формулы (8.13) необходимо знать основы калибровки валков при прокатке сортовых и фасонных профилей. Например, абсолютное обжатие при прокатке в калибрах вычисляют по формуле:

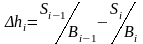, (8.14)

где S_i-1, S_i – площади поперечного сечения прокатываемого профиля до и после обработки в i-й клети; B_i-1, B_i – максимальная ширина поперечного сечения профиля до и после его прокатки в i-й клети.

Таким образом, отношения ; в формуле (8.14) представляют собой условные толщины на входе h_i-1 и на выходе h_i, если реальный профиль заменить так называемой приведенной полосой, имеющей плоское поперечное сечение.

Длину очага деформации при прокатке в калибрах вычисляют по формуле:

, (8.15)

где R_Кi – это так называемый катающий диаметр валка в i-й клети, равный:

, (8.16)

где D_i = номинальный (наружный) диаметр бочки валка в i-клети (до того, как в ней производят “врезку” калибров).

Например, если, с учетом формул (8.14) – (8.16), R_Кi=400мм,

h_i-1=100мм, h_i=70мм и μ_i=0,5, по формуле (8.13) получим: n_К=1,25. По данным Г.С. Никитина, возможный диапазон значений n_К=1…2. При прокатке на гладкой бочке n_К=1.