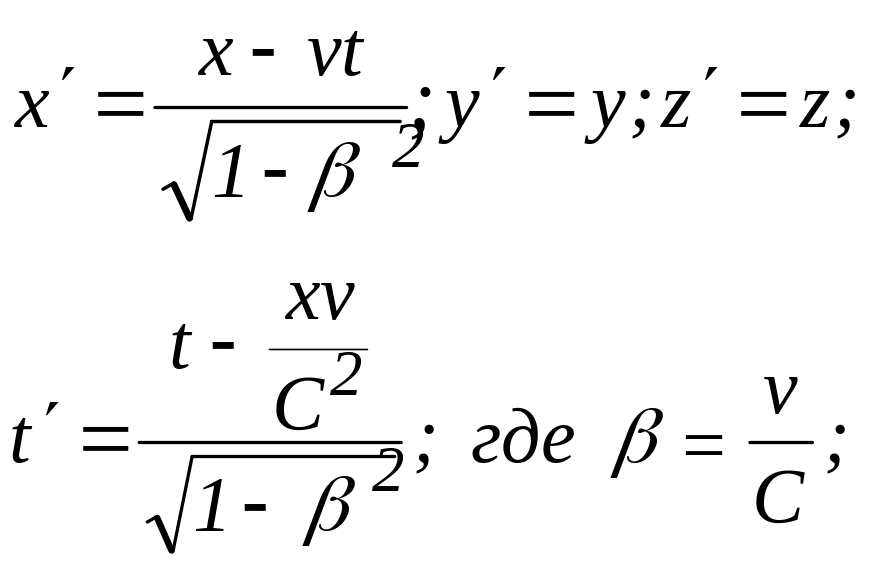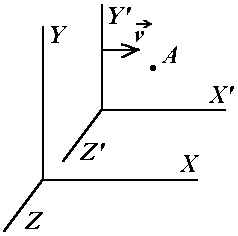Контрольные вопросы

1. Возможно ли проведение исследований, аналогичных описанным, если исследуемый фактор имеет не только качественное выражение, но и количественную градацию?

2. При отсутствии достоверных опытных результатов в подтверждение гипотезы о врожденной предрасположенности к преступному поведению - можно ли считать такую гипотезу окончательно опровергнутой? Ответ поясните.

3. Возможно ли исследование влияния на преступное поведение не биологических, а социальных и психолого-педагогических факторов?

Литература

1. Генетика и наследственность. Сб. под ред. Е.А.Яновской. Пер. с фр. М.: Мир, 1987. - С.191-193, 244-247.

2. Малиновский А.А. Биология человека. М.: Знание, 1983 (сер. “Биология”, № 8). - С.33 - 36.

3. Венчиков А.И., Венчиков В.Д. Основные приемы статистической обработки результатов наблюдений в области физиологии. М.: Медицина, 1974. - С. 52-59.

Практическая работа № 13

ПАРАДОКСЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

Раздел программы: Новейшая революция в естествознании.

Необходимые предварительные знания: Преобразования Лоренца.

Теоретическая часть

Годом создания специальной (или частной) теории относительности (СТО) считается 1905 г., когда ее автор А.Эйнштейн выступил с докладом “К электродинамике движущихся сред.” Эта теория стала обобщением ряда научных достижений, носящих революционный характер: эксперимента А.Майкельсона (1881), релятивистских преобразований координат для двух инерциальных систем отсчета (Х.Лоренц,1904г.) и некоторых других. Именно теоретическое осмысление экстраординарных научных фактов и знаменовало скачок в естественнонаучном развитии, получивший название новейшей революции в физике и охватившей затем другие науки о природе. Релятивистская физическая теория (механика) А.Эйнштейна наряду с квантовой теорией М.Планка - А.Эйнштей­на заложили основу физики и всего естествознания ХХ века. Вместе с тем, объяснительные и предсказательные функции СТО, касающиеся условий движения вещества с околосветовыми скоростями, для ученых, воспитанных в классических представлениях, выглядят явно парадоксально.

Ход работы

1. Запишите и объясните преобразования Лоренца, сопроводив их пояснительным чертежом.

Эти преобразования связывают координаты и моменты времени событий, происходящих в произвольной точке А, при их измерении в неподвижной системе отсчета XYZ и в системе XYZ, движущейся с постоянной скоростью v относительно первой вдоль оси Х.

2. Запишите или выведите обратные преобразования Лоренца, выражающие, в отличие от прямых преобразований, зависимости координат и времен в неподвижной системе отсчета от соответствующих характеристик в движущейся системе отсчета.

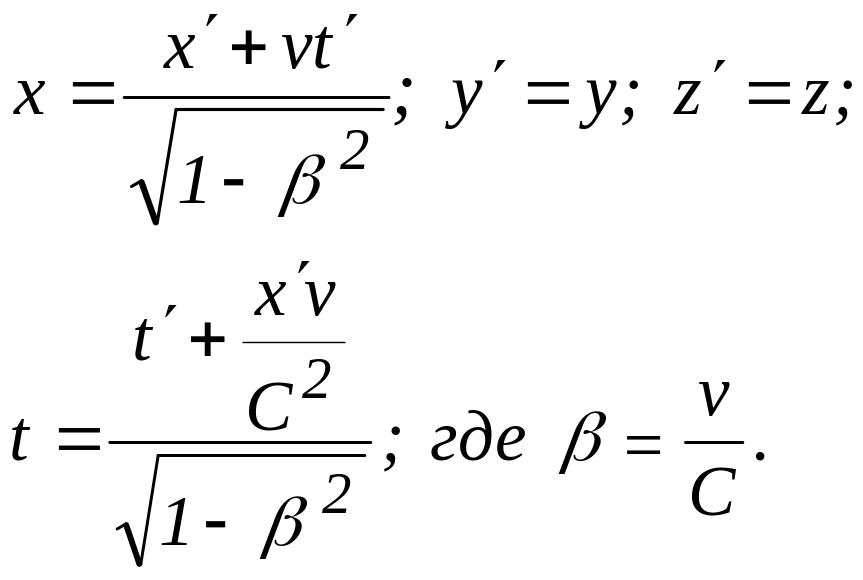
Ответьте, какую замену переменных следует произвести, чтобы из прямых преобразований Лоренца получить обратные самым простым способом?

Сравните полученный результат с результатом, вытекающим из тривиального преобразования формул (разрешение их относительно x и t). Вся СТО обязательно подразумевает существование двух вышерассмотренных инерциальных систем отсчета.

3. Выведите предельный случай преобразований Лоренца для v«С, или «1:

Эти преобразования носят название преобразований Галилея и известны из классической физики. Дайте словесное выражение преобразований Галилея и приведите примеры их действия.

4. Первый парадокс СТО называется парадоксом одновременности. Он формулируется следующим образом:

Два события, происходящие одновременно в разных местах одной системы отсчета, не являются одновременными в другой системе отсчета.

Если в движущейся системе XYZ происходят одновременно два события в разных точках, то

Из обратных преобразований Лоренца тогда следует, что t₁  t₂. Обоснуйте этот вывод. Затем проделайте аналогичное исследование для событий, одновременных в неподвижной системе отсчета, и запишите результат.

5. Второй парадокс СТО называется парадоксом длины. Он формулируется следующим образом:

Длина l тела, измеренная в неподвижной системе отсчета, и длина l' того же тела, измеренная в движущейся системе отсчета, не одинаковы и связаны соотношением:

Таким образом, длина движущегося тела сокращается (при измерении ее в неподвижной систем отсчета). Для доказательства воспользуйтесь предыдущим парадоксом (п.4) и запишите:

Здесь учтено, что координаты х₁ и х₂ измеряются одновременно, т.е. t₁= t₂. Объясните, почему для вывода были использованы прямые преобразования Лоренца.

6. Третий парадокс СТО называется парадоксом времени. Он формулируется следующим образом:

Время t протекания процесса в движущейся системе отсчета и время t протекания этого же процесса в неподвижной системе отсчета не одинаковы и связаны соотношением:

Таким образом, темп протекания времени в движущейся систем отсчета замедляется (в сравнении с темпом тех же процессов в неподвижной системе отсчета).

Для доказательства воспользуйтесь следующим расчетом. Пусть в точке x’, неподвижной в системе X’Y’Z’, протекает процесс длительностью . Используя обратные преобразования Лоренца, получаем:

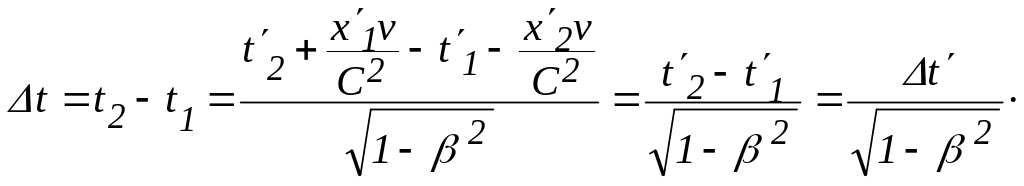
Мы учли, что процесс протекает в одной точке, т.е. x’₁ = x’₂ = x’.

Объясните, почему для данного вывода были использованы именно обратные преобразования Лоренца.

7. В заключение получите численные оценки рассмотренных эффектов для следующих гипотетических условий:

А. Космический корабль длиной 100 м летит со скоростью 2,97х10⁸м/с относительно Земли. Какая длина корабля будет наблюдаться с Земли?

Б. Из двух двадцатилетних близнецов, Тима и Тома, второй остается на Земле, а первый совершает полет (со скоростью 0,999 частей от скорости света) до ближайшей звезды Альфа Центавра, находящейся на расстоянии 4-х световых лет от Земли. По достижении звезды он сразу пускается в обратный путь и прилетает на Землю. Каков будет возраст каждого из близнецов при их встрече?

Это - так называемый в СТО “парадокс близнецов”.

Резюме

Учет в СТО релятивистских эффектов, математически представленных в преобразованиях Лоренца, приводит к неожиданным с точки зрения классической механики парадоксам. Однако ощутимое проявление этих парадоксов возникает только при очень больших скоростях движения объектов - близких к скорости света.