Ход работы

1. Исследуйте простейшую модель неограниченного роста численности популяции: , где х - численность популяции; k₁>0 - коэффициент пропорциональности.

Дайте словесную (смысловую) формулировку записанного математического выражения. Решите составленное дифференциальное уравнение.

Ответ:

Таким образом, в математическом виде рост популяции выражается экспоненциальной функцией от времени. Объясните смысл величины x₀.

Такой рост называется мальтузианским по имени Мальтуса Т.Р. - первого ученого, который его исследовал в 1798 г. Зарисуйте график мальтузианского роста и объясните его ход:

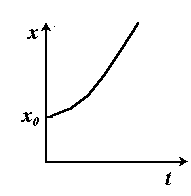
2. Исследуйте простейшую модель неограниченного спада численности популяции:

Дайте словесную (смысловую) формулировку записанного выражения. Найдите решение приведенного дифференциального уравнения.

Ответ:

График спадающей экспоненты выглядит следующим образом:

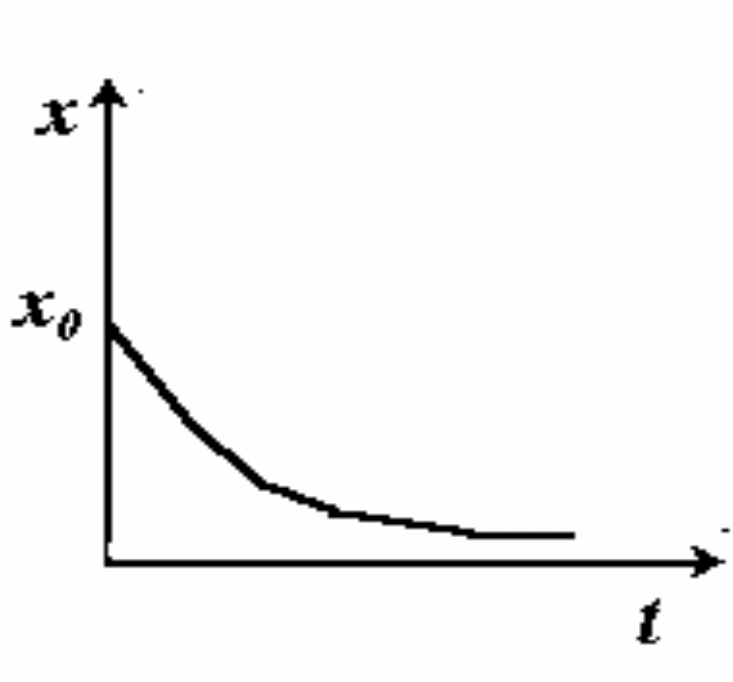
3. Исследуйте общий случай простейшей модели динамики популяции при наличии рождаемости и смертности:

Решение уравнения очевидно:

Выведите условия для частных случаев динамики:

а) неограниченного роста популяции;

б) неограниченной ее убыли;

в) стационарности, т.е. постоянства численности.

Установите, является ли данное стационарное состояние численности популяции устойчивым или неустойчивым.

4. Исследуйте простейшую модель ограниченного роста численности популяции:

Дайте словесную (смысловую) формулировку записанного математического выражения и объясните на качественном уровне механизм ограничения (т.е. возникновения предела) роста численности популяции. Решите приведенное дифференциальное уравнение (нелинейное, первого порядка, с разделяющимися переменными). Удобно воспользоваться табличной формулой неопределенного интеграла:

Ответ:

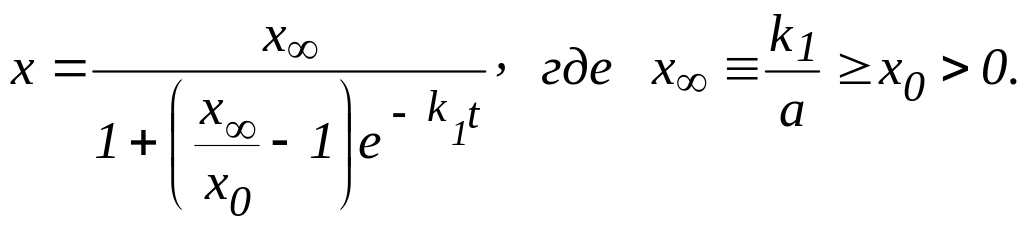
Объясните смысл величин x₀ и x_ .

Указанную функцию x(t) принято называть логистической (или логистикой), а сам рост - логистическим. Графический вид решения уравнения следующий:

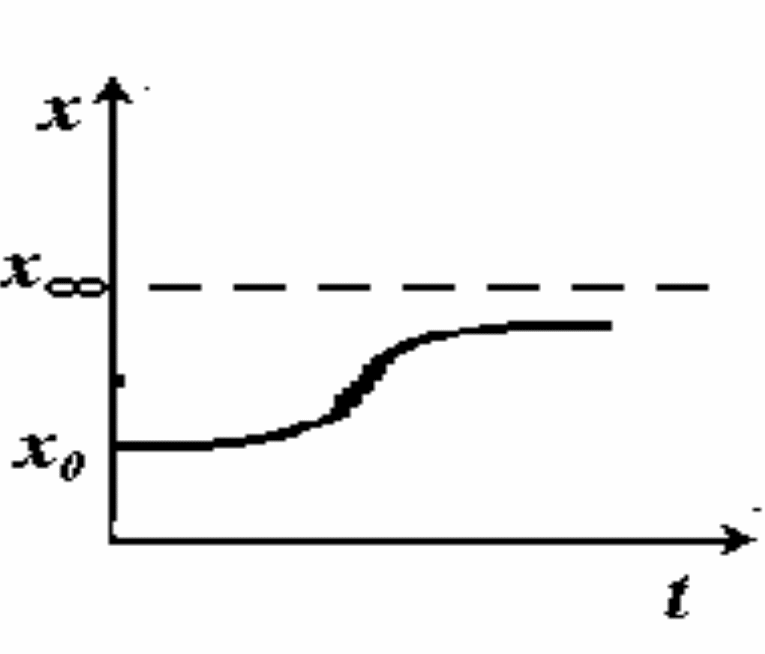
5. Исследуйте простейшую модель ограниченного спада численности популяции:

Дайте словесную (смысловую) формулировку записанного математического выражения и объясните механизм ограничения спада численности популяции. Запишите решение приведенного дифференциального уравнения:

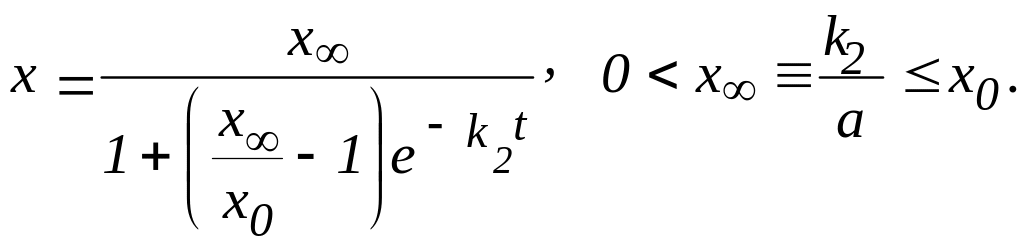
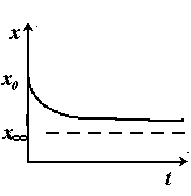
Такую функцию, как и ранее приведенную, называют логистической, но, в отличие от первой, спадающей, или обратной. Ее график следующий:

6. По аналогии с п.3 исследуйте обобщенную математическую модель ограниченного роста численности популяции:

Знак в скобках зависит от знака k : он противоположен ему. Поэтому модуль (абсолютная величина) двучлена в скобках при ограниченном росте меньше, чем при неограниченном.

По аналогии с п.3 выясните характер стационарности (устойчивая или неустойчивая) при k=0.

7. Рассмотрите на качественном уровне более сложный случай, когда ограничения роста и спада взаимообусловлены у двух популяций, находящихся в отношениях типа "хищник-жертва":

Объясните роль каждого из членов системы уравнений как отражения взаимоотношений внутри и вовне популяций (модель Вольтерра).

Решение этой системы нелинейных дифференциальных уравнений в общем случае можно найти лишь приближенно. Математические подходы к этому решению будут изучаться во второй части данной темы. Графически решение для общего случая представляется в следующем виде:

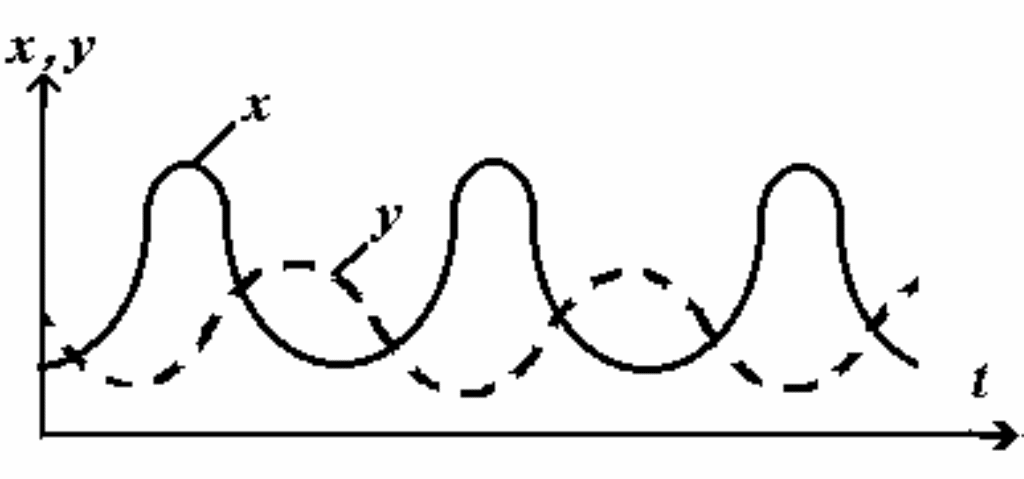
Объясните на качественном уровне ход кривых и обоснуйте это с биологических позиций.

Резюме

Основными режимами популяционной динамики являются: рост (неограниченный или ограниченный), спад (неограниченный или ограниченный) и колебания (ритмы) численности.