Ход работы

Примечание: В работе используется наша модификация физической модели ритмов популяций (известных еще под названием "хищник-жертва"), созданной Дж.Т. Томпсоном и описанной в научной литературе [1]. В отличие от модели Томпсона, наша модификация не требует специального реквизита и проста в процедурном отношении.

1. Используйте для занятия шахматную доску, у которой в раскрытом состоянии нет просвета и уступа между 4-й и 5-й горизонталями, а также два набора плоских дискообразных фишек разного цвета. Фишек каждого цвета желательно иметь не менее 100 штук, они должны быть совершенно одинаковы по размеру и форме. Диаметр фишки не должен превышать половины (а лучше - трети) стороны клетки доски. Таким образом, в пределах клетки должно умещаться несколько фишек. В качестве фишек модели можно использовать не только фишки от настольных игр, но и пуговицы, монеты и т.п. предметы.

Оптимальным условием для проведения занятия является такое, когда одной моделью пользуются два студента, взаимно помогая и контролируя друг друга.

2. Усвойте и запишите в тетрадь правила моделирования, т.е. правила "игры":

1) в заданном исходном соотношении "хищники", или "лисы" (например, фишки черного цвета) и "жертвы", или "зайцы" (фишки белого цвета) тщательно перемешиваются и равномерно распределяются по "ареалу обитания" (игровому полю);

2) положения фишек, относящиеся к двум или четырем соседним клеткам доски, корректируются перемещением фишки в одну, превалирующую клетку;

3) "лисы", попавшие на черные клетки, если там нет "зайцев", "вымирают" из-за отсутствия "пищи" (т.е. снимаются с доски);

4) "зайцы", попавшие на белые клетки, ели там нет "лис", "размножаются" (т.е. удваиваются по числу);

5) "лисы", попавшие на одну клетку с "зайцами", “пое­дают” последних и "размножаются" (т.е. фишки "зайцев" снимаются с доски, а фишки "лис" удваиваются на занятых ими полях);

6) после выполнения всех правил игровой цикл (тайм) повторяется с использованием оставшихся фишек.

3. Выполните не менее 30-ти игровых циклов (таймов) с наборами фишек, каждый раз фиксируя в тетради результат очередного тайма. Исходное соотношение фишек задается преподавателем (например, 10 : 20 "лис" и "зайцев" соответственно). Оно может быть разным или одинаковым для всех пар студентов.

4. Зарисуйте графики динамики ритмов популяции, реализованных на вашей модели. Их удобно разместить по всему тетрадному листу.

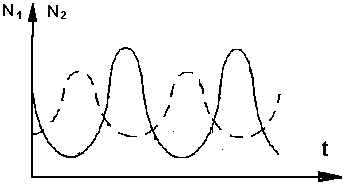
Ориентировочный вид графиков показан на ри­сунке. По оси ординат от­ложены численности, по оси абсцисс – таймы. – – – – “зайцы” –––– – “лисы”

5. Проанализируйте представленные на графиках результаты и запишите выводы, ответив на вопросы:

1) какой ритм - хищников или жертв - является опережающим?

2) одинаковы ли периоды ритмов хищников и жертв?

3) являются колебания численности популяций гармоническими (т.е. синусоидальными по форме)?

Попытайтесь дать объяснения на качественном теоретическом уровне полученным эмпирическим закономерностям, отраженным в графиках.

Резюме

Физическое моделирование ритмов популяций (типа "хищник - жертва") легко позволяет установить основные закономерности этой динамики не только в качественном, но и в количественном отношении.

Контрольные вопросы

1. Каким образом в рассмотренной модели реализуется взаимодействие между популяциями?

2. Зависит ли период ритма популяций от исходного соотношения их численностей?

3. Возможен ли, в принципе, другой исход реализации модели, кроме ритма? Ответ обоснуйте.

4. Какой тип пищевой связи (жесткий или гибкий) реализован в данной модели?

Литература

1. Томпсон Дж.М.Т. Неустойчивости и катастрофы в науке и технике. М.: Мир, 1985. - С. 143 -148.

2. Романовский Ю.М. и др. Что такое математическая биофизика. М.: Просвещение, 1971.- С. 81 - 88.

3. Волькенштейн М.В. Физика и биология. М.: Н.,1980. - С. 101 -104.

Практическая работа № 22

МОДЕЛИРОВАНИЕ ДИНАМИКИ ПОПУЛЯЦИЙ

Часть 1

Разделы программы: Роль математики в науке. Ритмическая самоорганизация материи.

Необходимые предварительные знания: Обыкновенные дифференциальные уравнения. Модель Вольтерра.

Теоретическая часть

Математическое моделирование - один из самых эффективных теоретических методов, применяемых в естественнонаучном познании. Оно позволяет с необходимой точностью осуществить все основные функции научной теории - описать, объяснить и спрогнозировать изучаемое явление. Более того, по мере углубления изучения моделируемого объекта математическое моделирование позволяет реализовать широкий диапазон своих возможностей для все более точной подгонки модели к объекту. В частности, использование современной электронной вычислительной (компьютерной) техники позволяет в большинстве случаев достичь высокой степени соответствия модели и объекта, даже если исходное приближение является весьма грубым.

Изучение численности популяций и ее изменений со временем (т.е. динамики) в зависимости от различных факторов - один из самых развитых разделов математического моделирования. Он находит применение в экологии, микробиологии, паразитологии, общей биологии, биогеоценологии и в ряде других естественнонаучных дисциплин.