Ход работы

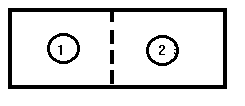
1. Исследуйте случай системы из двух частиц (№№ 1 и 2), свободно перемещающихся в замкнутом объеме и могущих занимать левую (Л) или правую (П) половины сосуда.

	_ _ _ - условная граница раздела половин сосуда
Л П

Результаты исследования отразите в таблице 1:

Примечания: 1. Эту и аналогичные последующие таблицы стройте в левой половине тетрадного листа, оставляя справа свободные места. Они будут заполняться в дальнейшем.

2. Обозначения: n_i - число состояний. P_i - их вероятность.

2. Проделайте аналогичное исследование для систем из трех и четырех частиц соответственно. Результаты отразите таблицах 2 и 3. Положение частиц достаточно отражать в таблицах только цифрами (без кружков, точек и т.п.).

3. Установите математическую закономерность для общего числа состояний N=n_i системы, состоящей из конкретного числа частиц. Сопоставьте эту зависимость с ранее установленной зависимостью числа состояний системы от числа ее элементов и числа состояний каждого элемента (см. практическую работу “Информационный подход в естествознании”, часть I). Сделайте вывод. Рассчитайте значения N для системы из 5, 10, 100 частиц (последнее можно оценить приближенно).

4. Усвойте рациональный подход для ускоренного выполнения расчетов определенных состояний системы, состоящей из конкретного числа частиц. Он основан на использовании комбинаторики - раздела математики дискретных величин.

Согласно комбинаторике случаи попадания m частиц из их общего количества n в левую половину сосуда могут быть рассчитаны нахождением числа сочетаний (“С”) из n по m: В этой формуле, очевидно, числа сомножителей в числителе и знаменателе дроби равны. Произведение последовательности m натуральных чисел обозначается m! (“эм факториал”). Таким образом:

Из комбинаторики также известны правила :

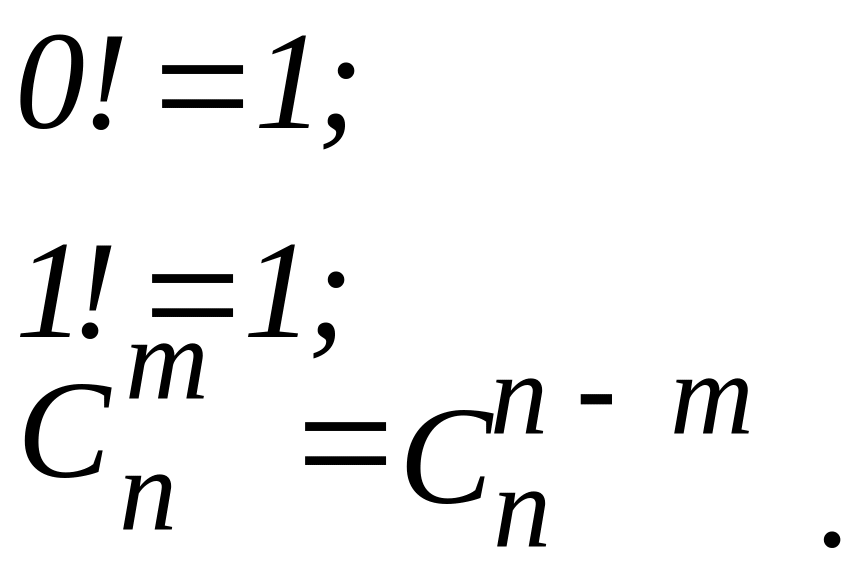
Таким образом, попадание в левую половину трех частиц из четырех может быть осуществлено числом вариантов:

Такое число вариантов имеет место и для одной частицы:

Следовательно, расчеты можно проводить как по левой, так и по правей половинам сосуда. Произведите эти расчеты для систем из двух, трех и четырех частиц и приведите их справа от соответствующих строчек таблиц №№ 1,2,3. Сделайте вывод.

5. Исследуйте систему из пяти частиц, заполнив таблицу № 4 и применяя рациональный способ расчета. При этом в таблице, расширенной для внесения выкладок, достаточно оставить всего два столбца: ”n_i” и “P_i”.

6. Проанализируйте полученные результаты:

А. Установите закономерность изменения вероятности реализации высокоупорядоченного состояния ( все частицы - в одной половине сосуда) с ростом числа частиц в системе: (Р_i)_min.

Б. Установите закономерность изменения вероятности реализации неупорядоченного состояния (частицы поровну распределены по частям сосуда) с ростом числа частиц: (Р_i)_max .

В. Установите закономерность изменения отношения (Р_i)_max /(Р_i)_min с ростом числа частиц.

7. Сделайте вывод о динамическом поведении закрытой системы, т.е. изменении ее состояния с течением времени. Считая все состояния равновероятными, отдельно отметьте тенденцию к снижению упорядоченности и тенденцию к увеличению флуктуаций около неупорядоченного состояния.

Резюме

Закрытая система в динамическом поведении стремится снизить свою внутреннюю упорядоченность до минимально возможной (т.е. увеличить беспорядок до максимального предела). Эта тенденция становится все более выраженной с ростом числа элементов системы. Математически это выражается через закон роста энтропии (S)в изолированной системе (формула Больцмана): S=k ln N, где k=1,3810 ^-23 Дж/К - постоянная Больцмана.

Одновременно с ростом числа элементов системы возрастает и вероятность флуктуаций вблизи неупорядоченного состояния.