6.10.4 Полярные и биполярные координаты

Задача определения положения точек местности, относительно какой-либо точки, принятой за начальную решается с помощью системы полярных координат (см. подраздел 6.10.1).

Полярные координаты – угол направления (угол положения) на определяемую точку, измеряемый по ходу часовой стрелки от полярной оси и расстояние (дальность) от полюса до этой точки однозначно определяют положение точки на плоскости относительно начала координат точки О (рисунок 117). Система полярных координат проста и может быть построена в любой точке местности, принятой за полюс. Углы и расстояния на местности, необходимые для определения местоположения объектов (целей) в этой системе при небольших расстояниях измеряют с помощью приборов наблюдения. Поэтому система плоских полярных координат широко применяется при засечке целей с одного наблюдательного пункта, целеуказании, ориентировании и т. п. При необходимости линейные и угловые измерения выполняют специальные дальномерами и угломерными приборами (устройствами). Полярной осью в этой системе координат может служить линия геодезического (астрономического) меридиана, магнитного меридиана, вертикальная линия координатной сетки на карте или принятое за начальной направление на удаленный ориентир на местности.

Рисунок 117 – Полярные координаты точки А: ά – дирекционный угол направления на точку А; Д – дальность до точки А

Полярные координаты точки на плоскости называются плоскими полярными координатами, а точки на референц-эллипсоиде – геодезическими полярными координатами. Положение точки на эллипсоиде относительно полюса определяется длиной геодезической линии S от полюса до определяемой точки и геодезическим азимутом А ее направления в точке, принятой за полюс. Геодезические полярные координаты определяют местоположение различных объектов, удаленных от полюса на значительное расстояние. Они широко применяются в различных видах топографических съемок.

Б

Рисунок 118 – Биполярные координаты точки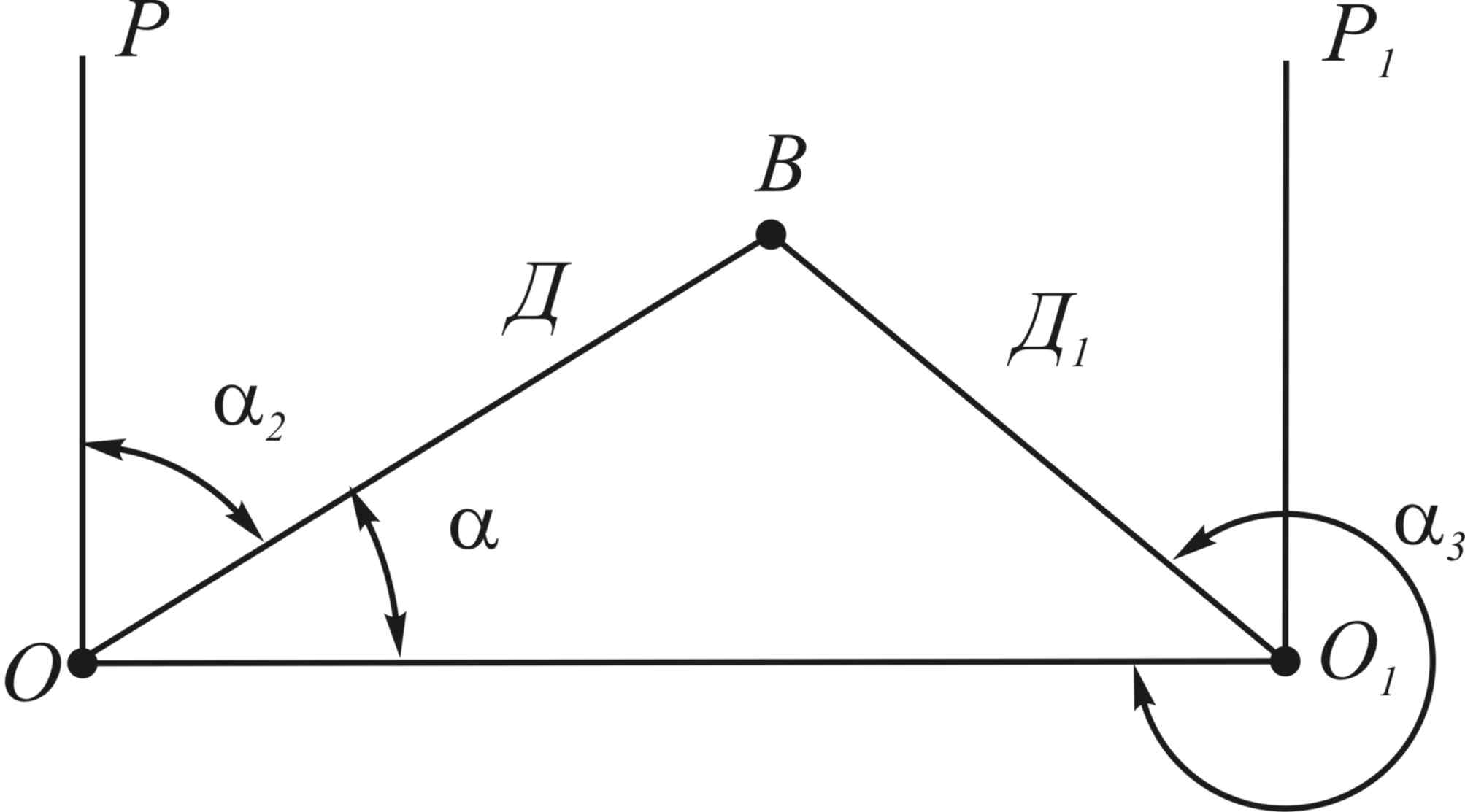

иполярные координаты. Рисунок 118 – это две линейные или угловые величины, которые определяют положение точки на местности или карте относительно двух точек (полюсов), принятых за наклонные. Биполярные координаты представляют собой разновидность полярных координат. Линейными величинами служат расстояния до определяемой точки оси полюсов, а угловые величины могут быть геодезические. Азимуты, магнитные азимуты, дирекционные углы, углы направлений которые измеряют от линии (базиса), соединяющей полюсы.

Биполярная система координат применяется при засечке проектных точек на местности, при определении границ земельных участков. Для более четкого определения местоположения точек указывают две угловые и две линейные величины.

6.10.5 Звездное небо

Небесная сфера. Звездное небо ночью из любой точки земной поверхности выглядит в виде полушара. Небесные светила удалены от Земли на огромные расстояния, поэтому наблюдателю кажется, что все они расположены на одной внутренней сферической поверхности этого полушара. Такая сферическая поверхность называется небесной сферой. Она имеет радиус произвольной длины, а центр ее находится в произвольной точке, в частности в точке наблюдения.

Воображаемая прямая линия, проходящая через центр небесной сферы параллельно оси вращения Земли, называется осью мира. Вокруг этой оси происходит видимое вращение небесной сферы с востока на запад, которое является следствием суточного вращения Земли вокруг своей оси с запада на восток.

Ось мира пересекает сферу в двух точках – Северном и Южном полюсах мира, являющихся неподвижными точками небесной сферы. Северный полюс мира Р находится вблизи Полярной звезды, а Южный Р1– около созвездия Октант. Чем ближе светило к Полюсу мира, тем меньше круг его суточного вращения.

Плоскость, проходящая через отвесную линию к поверхности Земли и ось мира, является плоскостью астрономического или истинного меридиана точки наблюдения, а след сечения этой плоскостью небесной сферы – астрономическим или истинным меридианом. Совершенно очевидно, что каждой точке на земной поверхности соответствует свой меридиан, а угол между направлениями на Полюс мира и на какой-либо предмет на земной поверхности является астрономическим азимутом. Способы определения азимута из астрономических наблюдений относятся к наиболее точным, так как расположение светил на небесной сфере и их видимое движение относительно сторон горизонта строго подчинено определенному закону движения небесных тел.

Созвездия. Для удобства ориентирования на звездном небе астрономы еще в глубокой древности разделили его на отдельные участки – созвездия (рисунок 119). В настоящее время насчитывается 88 созвездий. В Северном полушарии известны, например, созвездия Большая Медведица, Малая Медведица, Возничий, Орион, Лебедь, Лира, Кассиопея, а в Южном полушарии – Южный Крест, Большой Пес, Центавр и др.

Яркие звезды созвездий обозначаются буквами греческого алфавита, α некоторые из них, кроме того, имеют собственные имена, например Вега (α Лиры), Артур (α Волопаса), Полярная звезда (α Малой Медведицы).

Яркие звезды (их около 20) условились называть звездами 1-й величины, а наиболее слабые из доступных для наблюдения невооруженным глазом отнесены к звездам 6-й величины. Звезда Вега (созвездие Лиры) является самой яркой звездой северной, части небосвода. Она расположена вблизи Млечного Пути.

Небесные светила вращаются вокруг своей оси: и перемещаются в пространстве. Кроме собственного (истинного) движения светил имеет место видимое (кажущееся) для наблюдателя на Земле движение светил вследствие вращения Земли вокруг своей оси и вокруг Солнца. Годичный путь Земли, относительно Солнца называется эклиптикой. Чтобы безошибочно опознавать созвездия и отдельные звезды, надо изучить звездное небо. Вначале по карте звездного неба запоминают основные созвездия и их взаимное расположение. Легко опознается на небе созвездие Большой Медведицы, семь звезд которой составляют «ковш».

Рисунок 119 – Карта основных созвездий Северного полушария небесной

сферы

Если продолжить ручку «ковша» Большой Медведицы и на этом отрезке отложить расстояние, равное примерно длине всего «ковша», можно опознать звезду а созвездия Волопаса (Артур). Продолжив таким же образом ручку «ковша» Малой Медведицы и отложив расстояние, равное примерно двум длинам «ковша», в конце отрезка легко найти звезду α Возничего (Капеллу).

Таким образом, пользуясь картой звездного неба, можно опознать и использовать для ориентирования на местности то или иное созвездие или выбрать звезду для определения астрономического азимута.

Полярная звезда. Полярная звезда – яркая звезда из созвездия Малой Медведицы. Среди других звезд для наблюдателя она кажется неподвижной из-за близкого расположения к Северному полюсу мира. Угловое расстояние этой звезды от полюса в 1978 г. равнялось 50'. Ежегодно уменьшаясь вследствие прецессии оси вращения Земли в мировом пространстве, около 2100 г. оно достигнет наименьшего значения – 28'

Полярная звезда широко используется при ориентировании и определении местоположения. По наблюдениям Полярной звезды определяют склонение магнитной стрелки, поправки к показаниям буссолей, гирокомпасов и гиротеодолитов.

Контрольные вопросы и упражнения:

1. В чем различие между географическими и прямоугольными координатами точки на земной поверхности?

2. На какое расстояние удалена точка А с координатами х – 6885 км, у = 4852 км от точки В с координатами х=6852 км, у=4852 км?

3. На каком расстоянии к востоку или западу от осевого меридиана зоны находятся точки, имеющие координаты:

х_а =3 832 325, у_а = 6 352 683;

х_в =5 121 420, у_в =8 621 350;

х_с =4 835 740, у_с =22 422 138?

4. С какой максимальной точностью можно определять прямоугольные и геодезические координаты объектов по топографическим картам разных масштабов с помощью циркуля-измерителя и поперечного масштаба?

5. Прямоугольные координаты точки А: х=3831 км,у =21 583 км. Определить географические координаты этой точки с точностью до 1°.

6. Прямоугольные координаты исходной точки А (полюса):ха – 3 538 342, уо=6 344 535. Определить прямоугольные координаты точки В, если ее полярные координаты: а=60° и S=9350

7. Прямоугольные координаты х= 4 821355 у=3 837 434, а цели х=4 715 120, у=3 820 225. Определить полярные координаты цели.

1 Более подробно о системе высот будет сказано ниже.

11) Футштоком называется рейка с делениями, установленная так, что по ней можно сделать отсчёт, указывающий уровень воды.

1 Силой тяжести называется равнодействующая двух сил: силы притяжения Земли и центробежной силы суточного вращения Земли. Сила тяжести характеризуется величиной ускорения, которое она сообщает свободно падающему телу.

1 При отыскании дирекционного угла α_{1, 2} из точки В на точку А знаки приращений координат будут обратными: Δх = x₁ – x₂; Δу = y₁ – у₂.

1 При влажности грунта 50% (в обычном состоянии грун­ты имеют влажность 20%) -преодолеваемые уклоны меньше в 2 раза.

1 На проведение инженерных работ большое влияние оказывают приливы и отливы. Величина прилива различна: от 7 до 13м на Охотском море. Приливы изменяют уровень воды в реках, впадающих в моря. Приливная волна, входя в устье реки, может распространяться вверх по реке иногда на сотни километров, вызывая подьем уровня воды и противотечения. Скорость распространения приливной волны может достигать 20км/ч а высота 10м.