6.9 Измерения по карте

6.9.1 Измерение расстояний

При создании топографических карт, спроектированные на уровенную поверхность линейные размеры всех объектов местности уменьшают в определенное количество раз. Степень такого уменьшения называется масштабом карты.

Масштаб может быть выражен в числовой форме (численный масштаб) или в графической (линейный, поперечный масштабы) в виде графика. Оформление на карте численного и линейного масштабов показано на рисунке 100.

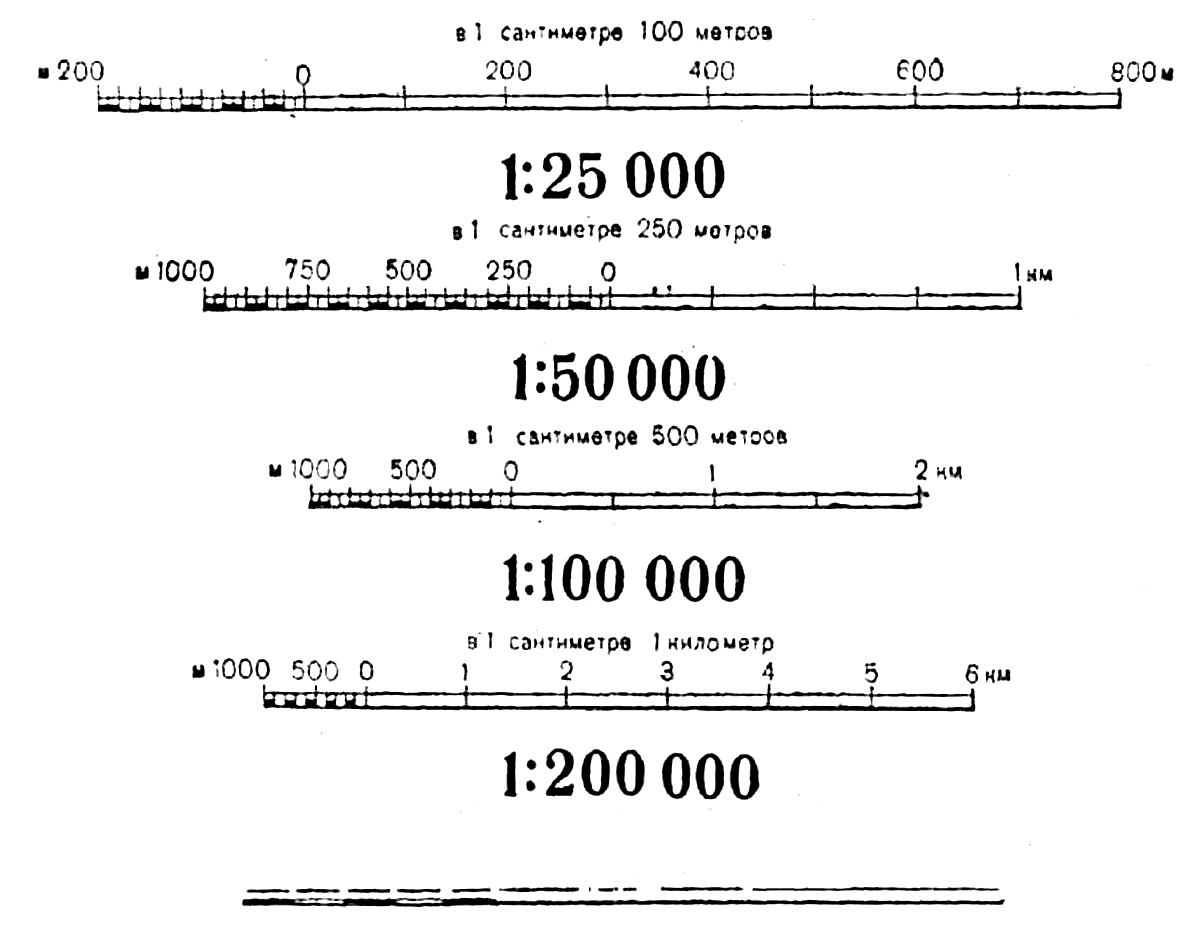
Рисунок 100 – Оформление численного и линейного масштабов на топографических картах

Расстояния по карте измеряют, пользуясь обычно численным или линейным масштабом. Более точные измерения выполняют с помощью поперечного масштаба.

Численный масштаб – это масштаб карты, выраженный дробью, числитель которой – единица, а знаменатель – число, показывающее, во сколько раз уменьшены на карте горизонтальные проложения линий местности. Чем меньше знаменатель, тем крупнее масштаб карты. Например, масштаб 1:25 000 показывает, что все линейные размеры элементов местности (их горизонтальные проложения на уровенную поверхность) при изображении на карте уменьшены в 25 000 раз

Расстояние на местности в метрах и километрах, соответствующее 1 см на карте, называется величиной масштаба. Она указывается на карте под численным масштабом.

При пользовании численным масштабом расстояние, измеренное на карте в сантиметрах, умножают на знаменатель численного масштаба в метрах. Например, на карте масштаба 1:50 000 расстояние между двумя местными предметами равно 4,7 см; на местности оно будет 4,7x500=2350 м. Если расстояние, измеренное на местности, необходимо отложить на карте, его надо разделить на знаменатель численного масштаба.

На пример, на местности расстояние между двумя местными предметами составляет 1525 м. На карте масштаба 1:50 000 оно будет 1525:500 = 3,05 см. Линейный масштаб представляет собой графическое выражение численного масштаба. На шкале линейного масштаба оцифрованы отрезки, соответствующие расстояниям на местности в метрах или километрах. Это облегчает процесс измерения расстояний, так как не требуется производить вычисления.

Измерения по линейному масштабу выполняют с помощью циркуля-измерителя (рисунок 101). Длинные прямые линии и извилистые линии на карте измеряют по частям. Для этого устанавливают раствор («шаг») циркуля-измерителя, равный 0,5 – 1 см, и таким «шагом» проходят по измеряемой линии (рисунок 102), ведя счет перестановок ножек циркуля-измерителя. Остаток расстояния измеряют по линейному масштабу. Расстояние подсчитывают, умножив число перестановок циркуля на величину «шага» в километрах и прибавив к полученной величине остаток. Если нет циркуля-измерителя, его можно заменить полоской бумаги, на которой черточкой отмечают измеренное на карте или откладываемое на ней по масштабу расстояние.

Поперечный масштаб – это специальный график, выгравированный на металлической пластинке (рисунок 103). Построение его основано на пропорциональности отрезков параллельных линий, пересекающих стороны угла. Стандартный (нормальный) поперечный масштаб имеет большие деления, равные 2 см, и малые деления (слева на графике), равные 2 мм. Кроме того, на графике имеются отрезки между вертикальной и наклонной линиями, равные по первой нижней горизонтальной линии 0,2 мм, по второй 0,4 мм, по третьей 0,6 мм и.т. д. С помощью поперечного масштаба можно измерять и откладывать расстояния на картах любого масштаба.

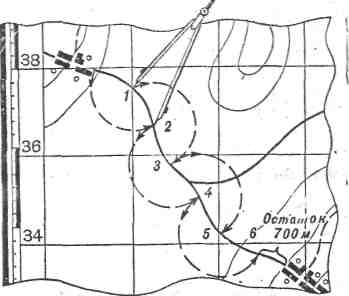
Рисунок 101 – Измерение расстояний на карте циркулем-измерителем по линейному масштабу

Рисунок 102 – Измерение расстояний по извилистой линии

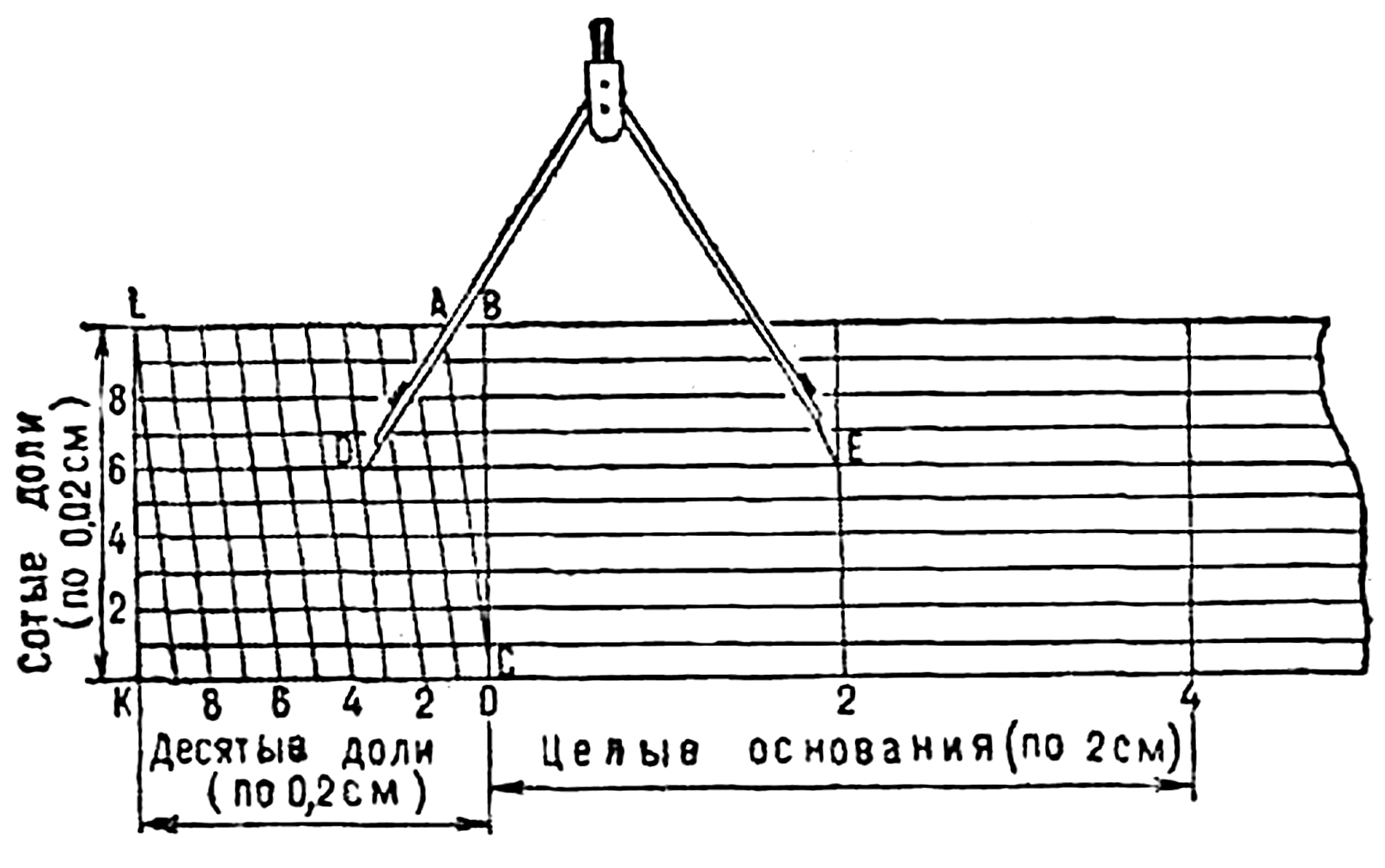
Рисунок 103 – Поперечный масштаб: отсчет по масштабу 2,36 см

Точность измерения расстояний. Точность измерения длины прямолинейных отрезков на топографической карте с помощью циркуля-измерителя и поперечного масштаба не превышает 0,1 мм. Эта величина называется предельной графической точностью измерений, а расстояние на местности, соответствующее 0,1 мм на карте, – предельной графической точностью масштаба карты.

Графическая ошибка измерения длины отрезка на карте зависит от деформации бумаги и условий измерения. Обычно она колеблется в пределах 0,5 – 1 мм. Чтобы исключить грубые ошибки, измерение отрезка на карте надо выполнять два раза. Если полученные результаты не расходятся более чем на 1 мм, за окончательное значение длины отрезка принимают среднее из двух измерений. Ошибки в определении расстояний по топографическим картам различных масштабов приведены в таблице 43.

Таблица 43 – Ошибки в определении расстояний по картам

Масштаб карты	Предельная графическая ошибка, м	Средняя ошибка
1:25 000 1:50 000 1:100 000 1:200 000 1:500 000 1:1000 000	2,5 5 10 20 50 100	12 – 25 25 – 50 50 – 100 100 – 200 250 – 500 500 – 1000

Поправка в расстоянии за наклон линии. Измеренное по карте расстояние на местности будет всегда несколько меньше. Это происходит потому, что на карте измеряют горизонтальные приложения, в то время как соответствующие им линии на местности обычно наклонные (рисунок 104). Коэффициенты перехода от измеренных на карте расстояний к действительным приведены в таблице 44.

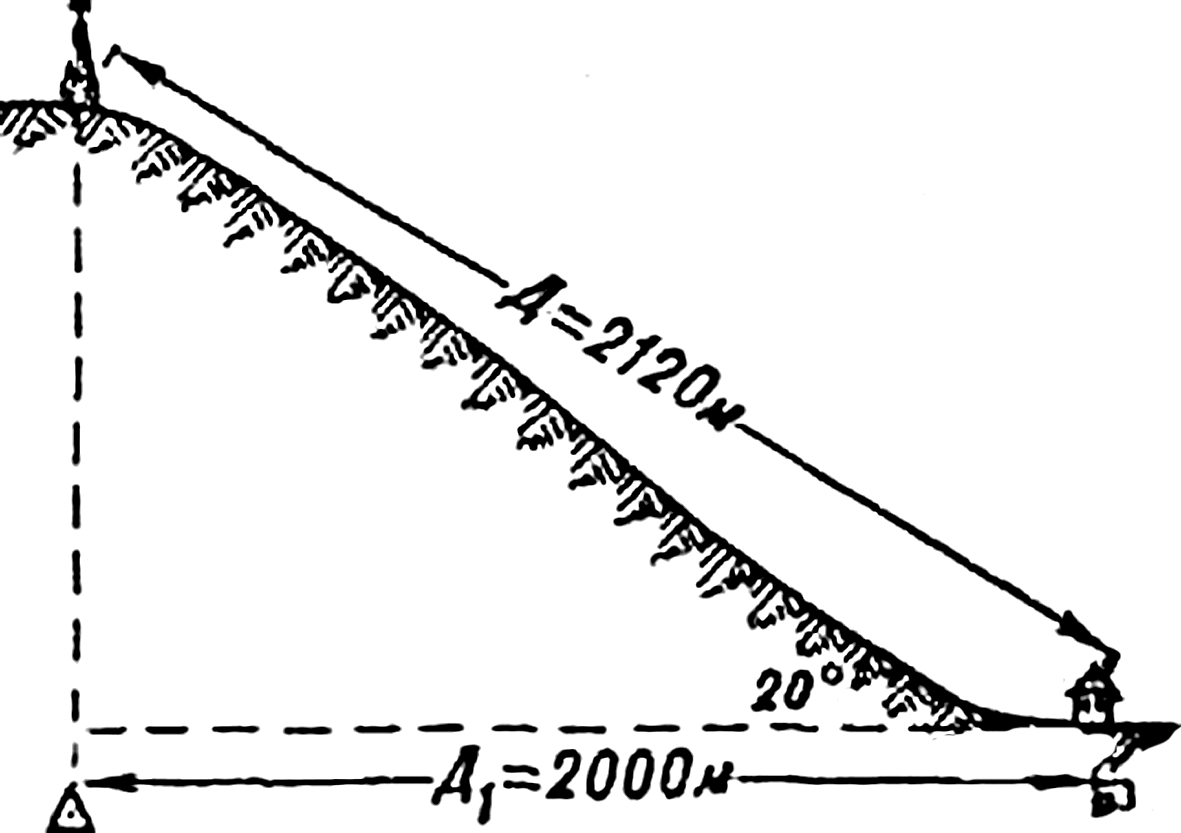
Рисунок 104 – Проекция длины ската на плоскость (карту):Д1 – расстояние на плоскости (карте); Д – расстояние на местности.

Как видно из таблицы, на равнинной местности измеренные по карте расстояния мало отличаются от действительных. На картах холмистой и особенно горной местности точность определения расстояний значительно снижается. Например, расстояние между двумя пунктами, измеренное по карте, на местности с углом наклона 12°, равно 9270 м. Действительное же расстояние между этими пунктами будет 9270х1,02=9455м.

Таблица 44 – Коэффициенты перехода расстояний

Угол наклона		Коэффициент перехода от длины линии на карте к расстоянию на местности
в градусах	в делениях угломера
0 6 12 18 24 30 36	0-00 1-00 2-00 3-00 4-00 5-00 6-00	1,00 1,01 1,02 1,05 1,10 1,15 1,24

Таким образом, при измерении расстояний по карте необхо­димо вводить поправки за наклон линий (за рельеф).

Определение расстояний по координатам, снятым с карты. Прямолинейные расстояния большой протяженности в одной координатной зоне могут быть рассчитаны по формуле.

(0)

где S — расстояние на местности между двумя точками, м;

х₁,y₁— координаты первой точки;

x₂,y₂ — координаты второй точки.

Этот способ определения расстояний используется при подготовке данных для проектирования сооружений в других случаях.