4.2.3 Отыскание грубых ошибок в полигонометрических ходах

Наличие грубых просчетов обычно подтверждается недопустимой величиной линейной и угловой невязок. Выявление точек и сторон хода, где допущен грубый просчет, проводится путем дополнительных вычислений.

Для обнаружения точки хода, на которой допущена грубая ошибка в измерении угла, вычисляют дирекционные углы и координаты точек хода сначала от исходного пункта N к пункту К (рисунок 60), а затем от пункта К к пункту N.

Рисунок 60 – Схема для нахождении ошибки в измерении угла при проложении полигонометрического хода

Угловая невязка в этом случае не распределяется.

При таком порядке вычислений координаты всех точек, полученные из «прямого» и «обратного» ходов, будут резко отличаться друг от друга, за исключением точки с ошибочно измеренным углом (значения координат этой точки, полученные из двух вычислений, будут очень близкими друг к другу). Угловые измерения на этой точке выполняют в полевых условиях заново, а для контроля измеряют углы и на соседних точках.

Для обнаружения стороны хода, в которой допущен грубый просчет при измерении линии, вычисления выполняют следующим образом: по уравненным дирекционным углам и измеренным сторонам вычисляются координаты точки К (рисунок 61), ошибочно определенные из-за просчета при измерении линий.

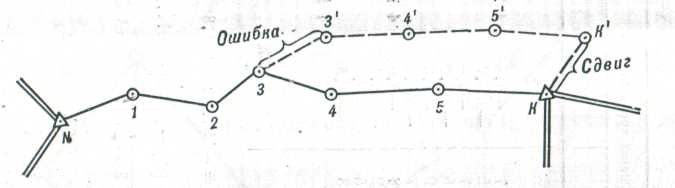
Рисунок 61 – Схема для нахождения ошибки в измерении сторон при проложении полигонометрического хода

Из решения обратной геодезической задачи по координатам точки К' и пункта К находят величину сдвига и дирекционный угол сдвига К К''. Вычисленный - дирекционный угол сдвига КК' будет близок (с точностью 1 – 5°) к дирекционному углу той стороны, в которой допущен просчет при измерении линии. Величина сдвига указывает величину ошибки.

Ошибочно определенная сторона снова измеряется на местности. При наличии нескольких сторон с близкими значениями дирекционных углов проводятся повторные измерения длин всех линий.

Отыскание ошибок указанными способами возможно при условии, что в полигонометрическом ходе допущен только один грубый просчет в измерении угла или линии. При наличии двух и более просчетов ошибки вычислениями не выявляются, и все полевые измерения повторяются заново.

4.2.4 Определение координат точек методом триангуляции

Определение координат точек методом триангуляции заключается в построении на местности системы смежных треугольников, вершинами которых являются определяемые и вспомогательные точки.

Треугольники могут образовывать ряды (рисунок 62), центральные системы (рисунок 63), сплошные сети. Отдельные точки могут определяться из вставок в треугольники (рисунок 64). При этом любая из принятых систем должна опираться, на две исходные стороны ГГС, а каждая из определяемых точек должна входить одновременно не менее чем в два треугольника.

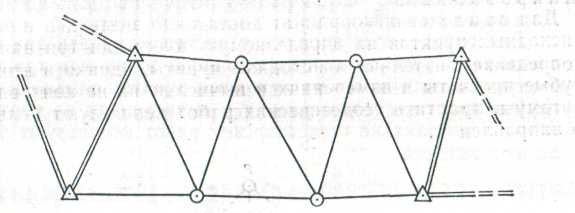
Рисунок 62 – Ряд треугольников

Частным случаем триангуляции при определении координат отдельных точек являются засечки, суть которых заключается в построении треугольников, образованных односторонними направлениями с исходных пунктов на определяемую точку или с определяемой точки на исходные пункты ГГС.

В зависимости от того, где выполняются измерения, различаются следующие виды засечек: прямая, обратная и комбинированная.

Для определения координат достаточно знать два направления с исходных пунктов на определяемую точку или три направления с определяемой точки на исходные пункты, однако в этом случае грубые просчеты в измерениях и вычислениях не контролируются, поэтому в практике геодезических работ используют большее число направлений.

Прямой засечкой координаты точки определяются по измеренным направлениям с трех и более исходных пунктов (рисунок 66).

Обратной засечкой координаты определяются по измеренным направлениям с определяемой точки на четыре и более исходных пункта (рисунок 67).

Комбинированной засечкой координаты точки, определяются по измеренным направлениям с одного исходного пункта на определяемую точку и по направлениям с определяемой точки на три исходных пункта (рисунок 68).

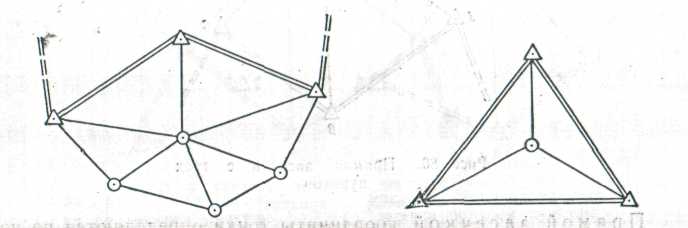
Рисунок 63 – Центральная система

Рисунок 64 – Вставка точки в треугольник

Все виды засечек в основном равноценны по точности, но несколько различаются по объему полевых измерений. При прямой засечке измерения выполняются на трех исходных пунктах. В комбинированной засечке измерения выполняются на одном исходном пункте и на определяемой точке. В обратной засечке полевые измерения выполняются только на определяемой точке.

Полевые работы при определении координат точек методом триангуляции включают рекогносцировку, закрепление точек на местности и измерение горизонтальных направлений. В процессе рекогносцировки проверяются сохранность центров и знаков на пунктах ГГС и видимость по всем запроектированным направлениям, уточняется местоположение точек. Как правило, одновременно с рекогносцировкой производится закрепление точек на местности.

Определяемые точки закрепляются специальными центрами. На точках устанавливаются переносные наружные знаки, а при необходимости строятся постоянные знаки в виде простых пирамид или вех.

Горизонтальные направления измеряются точными оптическими теодолитами. Порядок измерения горизонтальных направлений (углов) изложен в разделе 3.1.

Элементы приведения на исходных пунктах ГГС и точках, где установлены наружные знаки, определяются, как правило, графическим способом. Порядок определения элементов приведения изложен в разделе 3.1.

Рисунок 65 – Прямая засечка с трёх пунктов

Рисунок 66 – Обратная засечка по четырем пунктам

Рисунок 67 – Комбинированная засечка по трем пунктам

Вычислительные работы при определении координат точек методом триангуляции включают:

• обработку полевых материалов и предварительные вычисления;

• вычисление координат точек, определенных засечками;

• уравнивание триангуляции.

В ходе обработки полевых материалов и предварительных вычислений проводятся:

• проверка журналов измерения горизонтальных углов (направлений) и центрировочных листов;

• приведение измеренных направлений к центрам пунктов (точек) и на плоскость проекции Гаусса;

• уравнивание направлений на станции.

Приведение измеренных направлений к центрам пунктов и на плоскость проекции Гаусса, а также уравнивание направлений на станции осуществляются по формулам (13), (14), (17) и (18). Примеры вычисления приведены в таблице 22 и 23. Вычисление прямой засечки выполняется двумя способами:

• по котангенсам углов треугольников;

• по котангенсам дирекционных углов направлений.

Первый способ ограничений не имеет. Второй способ применяется в случае, когда значения дирекционных углов направлений находятся в пределах 5 – 85°, 95– 175^о, 85 – 265°, 275 – 355°.

Вычисление прямой засечки по котангенсам углов треугольников выполняется по формулам:

(0)

Контроль:

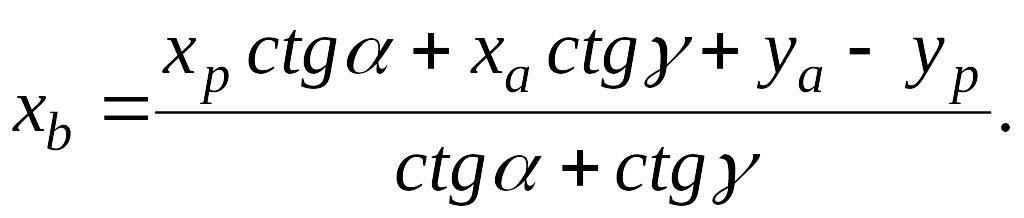(0)

Обозначение исходных пунктов и углов треугольника осуществляется по следующему правилу (рисунок 69): если смотреть с исходной стороны АВ на определяемую точку Р, то пункт, находящийся слева, обозначается буквой А, и внутренний угол при нем – буквой α, а пункт, находящийся справа, обозначается буквой В, и внутренний угол при нем – буквой β.

Обозначение исходных пунктов и углов треугольника осуществляется по следующему правилу (рисунок 70): если смотреть с исходной стороны АВ на определяемую точку Р, то пункт, находящийся слева, обозначается буквой А, и внутренний угол при нем – буквой α, а пункт, находящийся справа, обозначается буквой В, и внутренний угол при нем – буквой β.

За окончательное значение координат определяемой точки принимается среднее арифметическое из полученных результатов. Допустимые расхождения в значениях координат устанавливаются инструкцией. Пример вычислений приведен в таблице 25.

Рисунок 68 – К вычислению прямой засечки по котангенсам углов треугольников

Рисунок 69 – К вычислению прямой засечки по котангенсам дирекционных углов направлений

Таблица 25 – Вычисление прямой засечки по катангенсам углов треугольников

Название пункта (точки)	γ α β	xp xa xb	ctg α + ctgγ ctgγ ctg α ctg β ctg α + ctgβ	yp ya yb
P, № 0801 А,№ 671, пир. В,№ 660, пир. P, № 0801 А,№ 660, пир. В,№ 645, пир. ТЧК № 0801	120о15'33'' 35 45 5 23 58 42 180 00 00 82 07 57 43 33 07 54 18 56 180 00 00 Среднее	6 407 998,5 6 408 407,7 6 411 279,2 6 07 998,7 6 411 279,2 6 406 199,0 6 407 998,6	+ 0,805051 - 0,583 398 + 1,388 449 + 2,248 322 + 3,636 771 + 1,190 053 + 0,138 184 + 1,051 869 + 0,718 161 1,770 030	7 58 797,4 7 585 677,3 7 580 202,1 7 582 97,0 7 580 202,1 7 579 739,3 7 582 797,2

Вычисление прямой засечки по котангенсам дирекционных углов выполняется по формулам:

(0)

Контроль

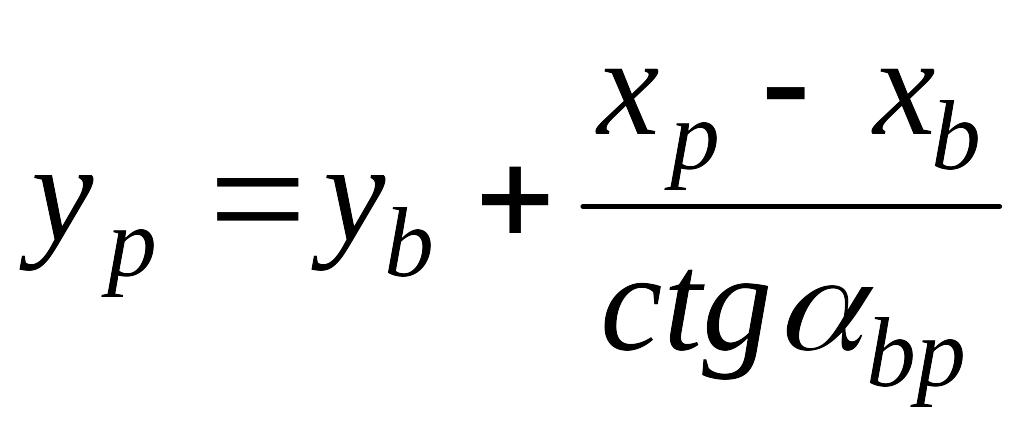(0)

где х_а, y_а, х_b, y_b – координаты исходных пунктов А и В;

х_p, y_p – координаты определяемой точки Р;

α_ap, α_bp – дирекционные углы направлений с исходных пунктов A и В на определяемую точку Р.

Обозначение исходных пунктов осуществляется по следующему правилу (рисунок 69): буквой В обозначается пункт, направление с которого на определяемую точку Р образует острый угол с направлением оси абсцисс х, второй пункт обозначается буквой А. За окончательное значение координат точки принимается среднее арифметическое из полученных результатов.

Пример вычисления приведен в таблице 26.

Таблица 26 – Вычисление прямой засечки по котангенсам дирекционных углов

Название пункта (точки)	αbp αap	xb xp – xb xp xp – xa xa xa – xp	ctg αbp ctg αap ctg αbp – ctg αap	yb yp – yb yp yp – ya ya ya – yp
В, № 660, пир. Р, № 0801 А, № 671, пир. В, № 660, пир. Р, № 0801 А, № 645, пир. ТЧК № 081	141o39'12'' 261 54 45 Среднее	6 411 279,2 - 3 280,7 6 407 998,5 - 409,2 6 408 407,7	- 1,26 410 + 0,14 210	7 580 202,1 + 2 595,3 7 582 797,4 - 2 879,9 7 585 677,3
		- 2 871,5 6 11 279,2 - 3 280,4 6 407 998,8 + 1 799,8 6 406 199,0	- 1,40 620 - 1,26 410 + 0,58 856	- 5 475,2 7 580 202,1 + 2 595,1 7 582 797,2 + 3 057,9 7 579 739,3
		- 5 080,2 6 407 998,6	- 1,85 266	+ 462,8 7 582 797,3

При прямой засечке в качестве визирной цели на определяемой точке, как правило, используются телескопические вышки и другие приспособления, что позволяет значительно расширить возможность использования данного метода. Если по каким-либо условиям вышку установить непосредственно над определяемой точкой невозможно, поступают следующим образом: выбирают две вспомогательные точки, симметричные относительно определяемой, на которых поочередно устанавливают вышку, и определяют их координаты. Тогда координаты определяемой точки Р будут

. (0)

Вычисление обратной засечки выполняют в следующем порядке:

– составляют схему обратной засечки (рисунок 70), на которой обозначают: буквой Р – определяемую точку; буквой В – исходный пункт; направление на который с точки Р образует более острый угол с осью абсцисс (X); буквой А – исходный пункт, лежащий слева от пункта В (если смотреть с точки Р); буквой С – третий исходный пункт; буквой D – контрольный пункт;

– вычисляют дирекционный угол α_ap стороны АР по формуле

, ( 0)

где х_а, y_a, x_b, x_c, y_c – координаты исходных пунктов ГГС;

α, β – значения измеренных углов на определяемой точке Р;

– вычисляют дирекционный угол α_bp стороны ВР по формуле

(0)

– вычисляют дирекционный угол α_ap стороны ВР по формуле (55) котангенсов дирекционных углов;

– для контроля вычислений по полученным координатам определяемой точки Р и координатам контрольного пункта D вычисляют дирекционный угол α_dp и длину S_dp стороны DP:

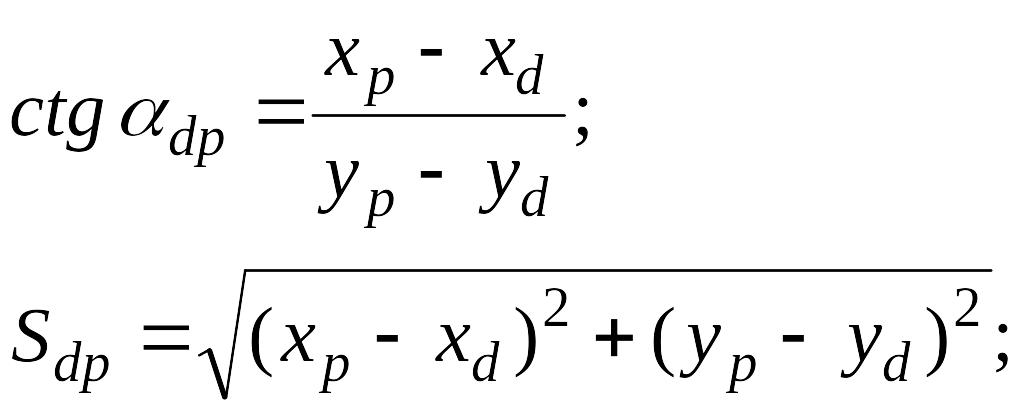(0)

– вычисляют ошибку положения определяемой точки Р относительно исходных пунктов

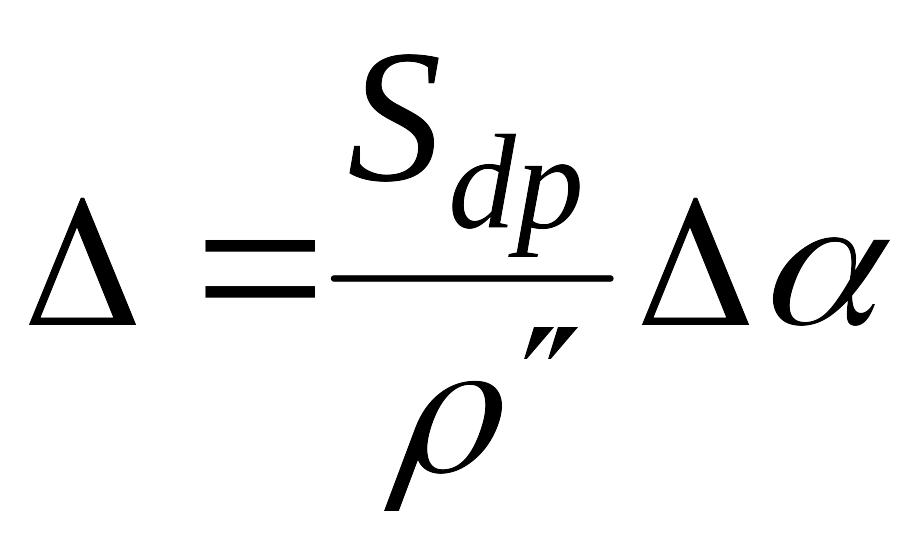(0)

где Δα = α_dp – (α_ap + γ);

ρ'' = 206 265.

Пример вычислений приведен в таблице 27.

Таблица 27 – Вычисление обратной засечки

Название пункта (точки)	Координаты		Результаты вычислений
	x	y
В, № 111, сигн. А, № 123, пир. С, № 131, сигн. D, № 118, пир.	4 122 300,1 4 116 067,1 4 124 171,3 4 118 577,3	5 158 001,4 5 159 568,7 5 165 096,0 5 166 752,5	α β γ	69о55'31'' 211 03 39 283 51 05	ctg α yb – ya ya – yc xc - xb	+ 0.36 545 - 1 567,3 - 5 527,3 + 1 871,7	ctg β xb – xa xa – xc yb – yc	+ 1,66 028 + 6 233,0 - 8 104,7 - 7 094,6
Р, № 2023	4 122 064,4 yконтр Δα Δ	5 162 154,3 5 162 154,3 + 6'' 0,17 м	Знам. αap αbp αbp + γ	- 78 77,9 23 19'20'' 93 14 51 307 10 25	yp – ya ctg αap ctg αbp Разн.	+ 2 585,6 + 2,31 950 - 0,05 674 - 2,37 624	xp – xd yp – yd ctg αdp αdp Sdp	+ 3 487,1 - 4 598,2 - 0,75 836 307о10'31'' 5,8 км

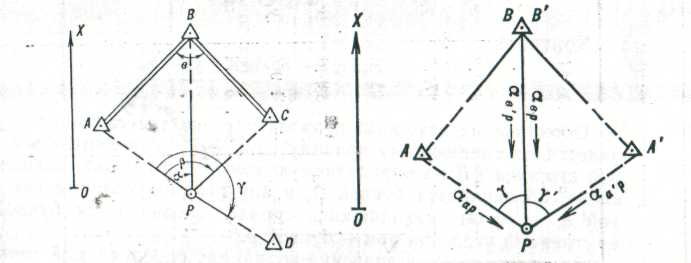
Рисунок 70 – К вычислению обратной засечки

Рисунок 71 – К вычислению комбинированной засечки

Вычисление комбинированной засечки выполняется двумя способами:

• по котангенсам углов треугольников;

• по котангенсам дирекционных углов направлений.

По котангенсам углов треугольников (рисунок 68) вычисление выполняют в следующем порядке:

• вычисляют значения углов треугольников β и α';

• вычисляют по формулам (53) координаты определяемой точки Р (пример вычисления приведен в таблице 25).

Вычисление по котангенсам дирекционных углов направлений (рисунок 69) выполняют в следующем порядке:

• вычисляют дирекционный угол с исходного пункта, где проводились измерения на определяемую точку (вычисления выполняются, как правило, одновременно с уравниванием за условие станции, пример вычисления приведен в таблице 28);

• вычисляют дирекционные углы направлений с двух других исходных пунктов на определяемую точку α_ap и α_a'р:

  αap = αbp + 180o – γ; αa'р = αbp + 180o + γ;

  (0)

• вычисляют по формулам (55) координаты определяемой точки Р (пример вычисления приведен в таблице 26).

Для отработки навыков в вычислении засечек рекомендуется первоначально вычисления производить с записью промежуточных действий. Уравнивание триангуляции осуществляется в следующем порядке:

Таблица 28 – Вычисление дирекционных углов направлений

Название направления	Дирекционный угол αисх	Приведение направления М	αисх - М	Δ	Уравненное направление Мур	Дирекционный угол направления α
№ 660, пир. № 671, пир. № 0801 № 645, пир.	117о40'30'',1 - 185 12 19,3	0о00'00'',0 23 58 40,3 67 31 45,7	117о40'30'',1 - 117 40 33,6	+ 1'',8 - - 1,7	0о00'00'',0 23 58 42,1 67 31 49,2	117о40'30'',1 141 39 12,2 185 12 19,3

• вычисляют значения углов, подсчитывают суммы углов треугольников, а также находят невязки каждого треугольника

(0)

• уравнивают углы треугольников путем распределения невязки каждого треугольника поровну на все три угла

(0)

• вычисляют дирекционные углы сторон триангуляции;

• вычисляют по теореме синусов длины сторон первого и последующих треугольников:

(0)

где b_i, c_i – определяемые стороны треугольника;

a_i – сторона треугольника, длина которой известна;

A_i, B_i, C_i – уравненные углы треугольника;

из решения последнего треугольника находят значение второй исходной стороны триангуляции и подсчитывают линейную невязку

(0)

где a_выч – вычисленное значение второй исходной стороны триангуляции;

а_исх – значение этой же стороны из каталога.

Полученную линейную невязку распределяют на все стороны пропорционально числу треугольников от начальной стороны триангуляции.

Координаты вспомогательных и определяемых точек находят последовательно из решения прямых геодезических задач по уравненным сторонам треугольников и их дирекционным углам. Координаты каждой точки вычисляют дважды и из полученных значений берут среднее. После вычисления координат конечного исходного пункта триангуляции вычисляют невязки:

(0)

Полученные невязки вводят в результаты вычислений, после чего вычисляют окончательные значения координат вспомогательных и определяемых точек.

Контрольные вопросы и упражнения:

1. Изложить сущность геодезического ориентирования.

2 Перечислить методы определения координат точек и рассказать их сущность.

3. Рассказать о порядке выполнения полевых работ при определении координат отдельных точек из системы полигонометрических ходов с одной узловой точкой.

4. Рассказать об общем порядке обработки результатов полевых измерений и вычисления системы полигонометрических ходов с одной узловой точкой.

5. Выполнить уравнивание результатов измерений на пункте ГГС № 117.

Название направления	Дирекционный угол исходной стороны αисх	Приведенное направление М
№ 118, пир. № 120, пир. Шт. 1	108о15'46'',3 221 28 59,6 -	0о00'00'',0 113 13 18,5 240 17 29,4

6. Вычислить угловую невязку отдельного полигонометрического хода, если:

α_Н = 262°17'30";

α_К = 226 10 01;

Σβ = 1656°07'40";

n = 10

7. Вычислить относительную линейную невязку полигонометрического хода, если W_x = – 1,2 м; W_y = 8,2; ΣS=9320 м.

8. Рассказать о порядке выполнения полевых работ при определении координат прямой засечкой. Рассказать об общем порядке вычисления прямой засечки.

9. Изложить общий порядок выполнения полевых работ при определении координат обратной и комбинированной засечками.

10. Координаты точки № 0882 определялись методом прямой засечки с трех пунктов ГГС. Вычислить координаты данной точки по котангенсам измеренных углов треугольников и котангенсам дирекционных углов направлений, если дано:

а) координаты трех исходных пунктов, и дирекционные углы направлений с исходных пунктов на определяемый;

Задача № 1

Название пункта	x1 x2 x3	y1 y2 y3	αap αbp αcp
№ 117 № 121 № 124	6 371 371,2 6 369 946,6 6 367 423,2	9 428 552,4 9 427 697,0 9 428 913,9	155о59 43'' 106 38 04 14 00 44

Ответ: x_ср = 6 369 433,1; у_ср = 9 429 415,5.

б) координаты трех исходных пунктов и внутренние углы при них;

Задача № 2

Название пункта	x1 x2 x3	y1 y2 y3	α1 β1 α2 β2
№ 117 № 121 № 124	6 371 371,2 6 369 946,6 6 367 423,2	9 428 552,4 9 427 697,0 9 428 913,9	54о59 34'' 75 39 01 47 37 10 39 45 30

Ответ: х_ср = 6 369 433,1; у_ср = 6 429 415,6.

11. Определить координаты точки № 0889 с трех пунктов ГГС прямой засечкой.

Измеренные направления:

№ 116, сигн.

№ 117, сигн. 0^о00'00"; 0889 24°30'59"; № 110, сигн. 188°45'10".

№ 108, пир.

№ 116, сигн. 0°00'00"; 0889 48°09'50"; № 114, сигн. 140°55'38".

№ 117, сигн.

№ 116, сигн. 0^о00'00"; № 118, сигн. 292°59'03"; 0889 309°16'28".

Исходные данные:

Название пункта	X Y	На какой пункт	Дирекционный угол
№ 108, сигн. № 116, сигн. № 117, сигн.	4 125 442,3 7 201 467,7 4 125 369,8 7 208 026,5 4 120 570,5 7 203 808,5	№ 116 № 114 № 117 № 110 № 116 № 108	90о37'58'' 231 33 36 221 18 43 50 03 45 41 18 43 334 17 53

Ответ: х_ср: = 4 123 276,0; у_ср = 7 203 360,2.

12. Определить координаты точки № 0774 комбинированной засечкой. Исходные данные:

№ 148, сигн.; х = 4 107047,0; у = 7148 515,2;

№ 154, пир.; x = 4 105 151,9; y =7 150 999,7

№ 152, сигн.; х = 4 099 765,1; y = 7 147 794,0.

Измеренные направления:

0774		№ 152, сигн.
№ 148, сигн. № 154, пир. № 152, сигн.	0о00'00'' 24 45 58 81 05 14	0774 № 148, сигн. № 154, пир.	0о00'00'' 79 34 51 104 40 54

Ответ: х = 4 100 444,1; y = 7 145 437,9.

13. Координаты точки № 0883 определялись обратной засечкой по четырем пунктам ГГС. Вычислить обратную засечку.

Задача № 1

Исходные данные:

№ 32, сигн. № 36, сигн.

х = 4 137 488,8; у = 4 472 286,0. х = 4 134 397,1; y = 7 485 130,6.

№ 34, пир. № 38, пир.

х = 4 135 931,0; у = 7 478 105,9. х = 4 127 829,9; у = 7 471 705,7.

Измеренные направления:

0883

№ 32, сигн. 0°00'00"; № 34, сигн. 45°16'01"; № 36, сигн. 68^o09'08";

№ 38, пир. 167°55'51".

Ответ: x = 4 130 805,7; y = 7 471 449,0.

Задача № 2

Исходные данные:

№ 63, пир. № 65, пир.

x = 4 127829,9; у = 7 471705,7. x = 4 121 217,8; y = 7478168,2.

№ 64, пир. № 67, сигн.

x = 4 128403,1; у = 7 479 515,1. x = 4 120 222,2; у = 7474010,2.

Измеренные направления:

0884

№ 63, пир. 0°00'00"; № 64, пир. 74°17'36"; № 65, пир. 132°.43'44";

№ 67, сигн. 171°51'54".

Ответ: х = 4 124 651,9; y =7 472 383,1.