2.3.3 Решение треугольника
Решением треугольника называется определение всех его сторон и углов по трем известным элементам, из которых хотя бы один должен быть его стороной.
Решение треугольника осуществляют по формулам соотношений его элементов, известных из курса тригонометрии.
Обозначив в треугольнике AВС (рисунок 31) стороны через а, в и с, а углы через А, В и С, запишем основные соотношения:
А + В + С = 180° (теорема суммы углов);
(теорема синусов);
а2 = в2 + с2 – 2·в·сcos A (теорема косинусов);
(теорема тангенсов)
и дополнительные соотношения:
Sin A = Sin· (B + C);
.
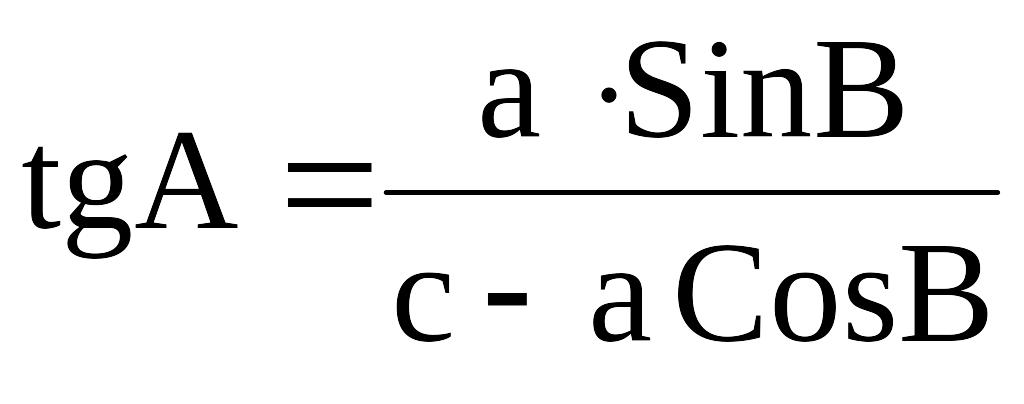Рисунок 31 – Треугольник
Пример. Пусть в треугольнике ABC (рисунок 31) известны сторона в и углы А и В. Необходимо найти угол С и стороны а и с.
Решение проводят в следующем порядке:
угол С находят по теореме суммы углов
С = 180о – (А + В);
стороны а и с вычисляют по теореме синусов
;
;
контроль вычислений осуществляют по формуле
.
Пример вычислений приведен в таблице 9.
Таблица 9 – Решение треугольника
-
№
действия
Элемент формулы
Величина
1
А
86о15'43"
2
4
5
В
С = [180o – (1) + (2)]
Контроль:
(1) + (2) +(4) = 180о
46о34'52"
47о09'25"
180о00'00"
6
7
8
Sin A
Sin B
Sin C
0,997 873
0,726 348
0,733 220
9
3
10
11
а = (3)
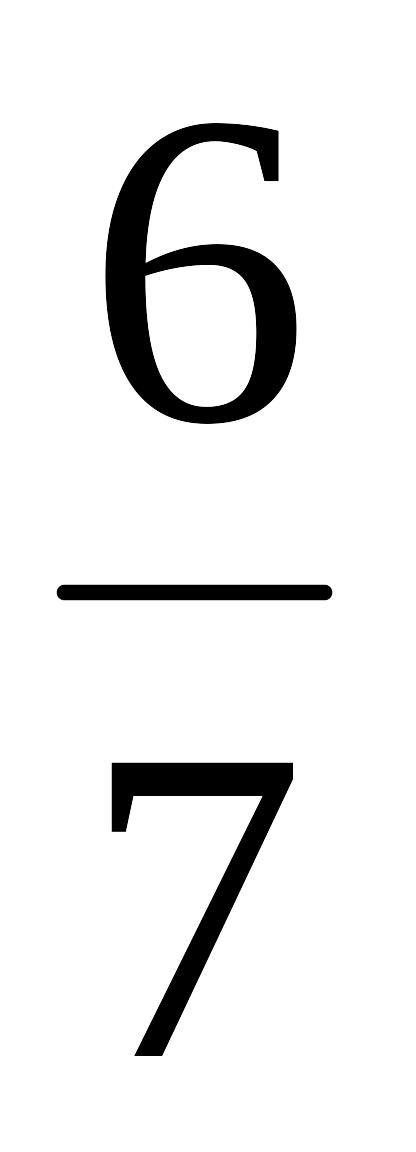
в
с = (3)
Контроль:
аконтр = (10)
6о448,3
4о693,7
4о738,1
6о448,3
Контрольные вопросы и упражнения:
1. Дать определение прямой и обратной геодезических задач.
2. Дать вывод формул решений прямой (обратной) геодезической задачи.
3. Решить прямую задачу по данным: x1 =6 104 172,8; y1 = 5 565 542,8;
s = 4 021,4; α1, 2 =57°57'54".
Ответ: x2 = 6 106 212,4; у2 = 5 568 802,5.
4. Решить обратную задачу по данным:
x1 = 6 114 133,5; х2 = 6 107 134,0; у1 = 5.565 596,8; у2 = 5 574 985,3. |
Ответ: α1, 2 = 126°42'21"; s =11710,5.
|
5. Решить треугольник по данным:
а) A = 86°49'11"; В = 36°52'12"; в = 7 211,2.
|
Ответ: С = 56°18'37"; а = 12 000,1; с = 10 000,1. |
б) а=5590,2; s = 9 340,7; С = 84°46'51". |
Ответ: с = 10 440,2; А = 32°13'26"; В = 62°59'43". |
в) а = 10 440,2; в = 12530,0; с = 8 944,2.
|
Ответ: А = 55°10'30"; В = 80°08'05"; С = 44°41 '25". |