2.3.2 Обратная геодезическая задача

Обратной геодезической задачей называется способ определения дирекционного угла и расстояния между двумя точками по известным их координатам.

Возвратимся к рисунку 30. Из условия обратной задачи известны: прямоугольные координаты точек А и В (х₁ и y₁; х₂ и y₂).

Необходимо найти расстояние s между точками А и В и дирекционный угол α_{1, 2} из точки А на точку В.

Решение. Искомые величины находят из соотношений прямоугольного треугольника ABC:

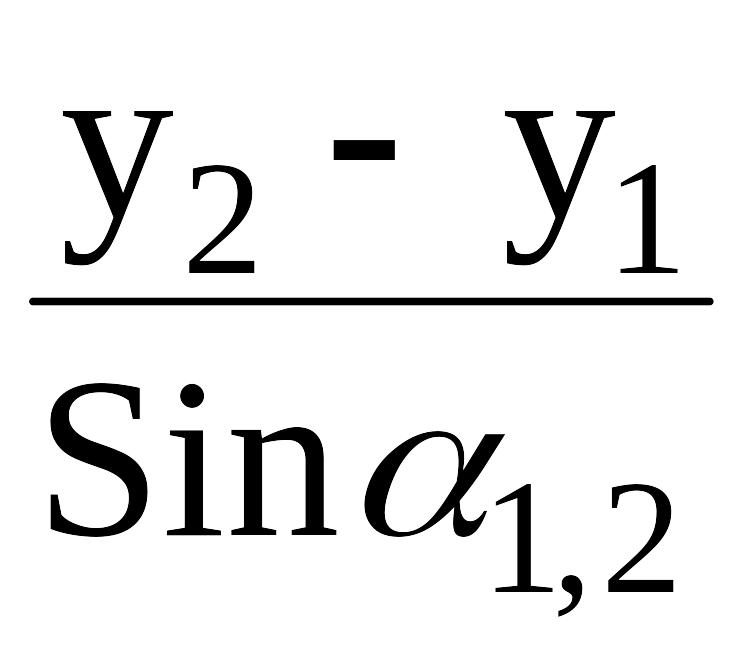tg α_{1, 2} = ; s= = =. (0)

По значению тангенса с помощью тригонометрических таблиц определяют величину только острого угла. Острый угол, отсчитываемый от ближайшего направления оси абсцисс (северного или южного) до направления данной линии, называется румбом и обозначается буквой r.

Для отыскания значения дирекционного угла по значению румба определяют четверть, в которой находится искомое направление.

Четверть, в которой находится направление АВ, определяют по знакам приращений координат Δх и Δу, вычисляемых как разности абсцисс и ординат:

Δх = x₂ – x₁; Δу = y₂ – у₁¹.

Формулы перехода от румба к дирекционному углу в зависимости от знака приращения координат приведены в таблице 7.

Таблица 7 – Переход от румба к дирекционному углу

Четверть круга	Знак приращения		Формулы перехода от румба к дирекционному углу
	Δх	Δу
I II III IV	+ – – +	+ + – –	α = r α = 180o – r α = 180o + r α = 360o – r

Искомое расстояние S определяют по формулам (10).

Наличие двух вариантов формул обеспечивает надежный контроль вычисления расстояния.

Вычисление расстояний и дирекционных углов при решении обратной геодезической задачи производят с использованием вычислительных машин и таблиц натуральных значений тригонометрических функций в следующем порядке, таблица 8:

Таблица 8 – Решение обратной геодезической задачи.

№ действия	Элементы формул	Величина
1	2	3
4 2 6 3 1 5 7 8	y2 у1. Δу = (4) – (2) x2 x1 Δх = (3) – (1) tg α1, 2 = (6) : (5) r	7 579 739,3 7 580 202,1 - 462,8 6 406 199,0 6 411 279,2 - 5 080,2 0,091 099 5о 12'19"

Продолжение таблицы 8

№ действия	Элементы формул	Величина
1	2	3
9 10 11 12 13 14	α1, 2 Sin α1, 2 Cos α1, 2 S1 S2 Sср	185о 12'19" 0,090 724 0,995 786 5 101,2 5 101,2 50 101,2

• выписывают координаты исходных пунктов. х₁, y₁, х₂, у₂ (действия 1 ‑ 4);

• вычисляют приращения координат Δх и Δу (действия 5 и 6); при этом всегда из координат второй точки алгебраически вычитают координаты первой точки;

• вычисляют тангенс дирекционного угла (действие 7);

• по тангенсу угла находят румб, который затем переводят в дирекционный угол с помощью таблицы 7, выбирают из таблиц синус и косинус этого угла (действия 8 – 11);

• дважды вычисляют расстояние s и за окончательное значение берут среднее из обоих результатов, при этом расхождение S₁ – S₂ не должно превышать более двух единиц последнего знака (действия 12 – 14).