2.2 Сведения о тригонометрических функциях

2.2.1 Тригонометрические функции острого угла

Тригонометрическими функциями острого угла называются числовые значения взаимного отношения любых двух сторон прямоугольного треугольника. В зависимости от того, отношения каких сторон прямоугольного треугольника рассматриваются (рисунок 28) тригонометрические функции носят названия: синус (Sin), косинус (Cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec).

Рисунок 28 – Прямоугольный треугольник

Синусом острого угла называется числовое значение отношения длины противолежащего катета к длине гипотенузы:

; .

Косинусом острого угла называется числовое значение отношения длины прилежащего катета к длине гипотенузы:

; .

Тангенсом острого угла называется числовое значение отношения длины противолежащего катета к длине прилежащего катета:

; .

Котангенсом острого угла называется числовое значение отношения длины прилежащего катета к длине противолежащего катета:

; .

Секансом острого угла называется числовое значение отношения длины гипотенузы к длине прилежащего катета:

; .

Косекансом острого угла называется числовое значение отношения длины гипотенузы к длине противолежащего катета:

; .

Тригонометрические функции острого угла связаны между собой математическими зависимостями. Так, например, тангенс произвольного острого угла х равен отношению синуса угла к косинусу

;

котангенс равен отношению косинуса угла к синусу

.

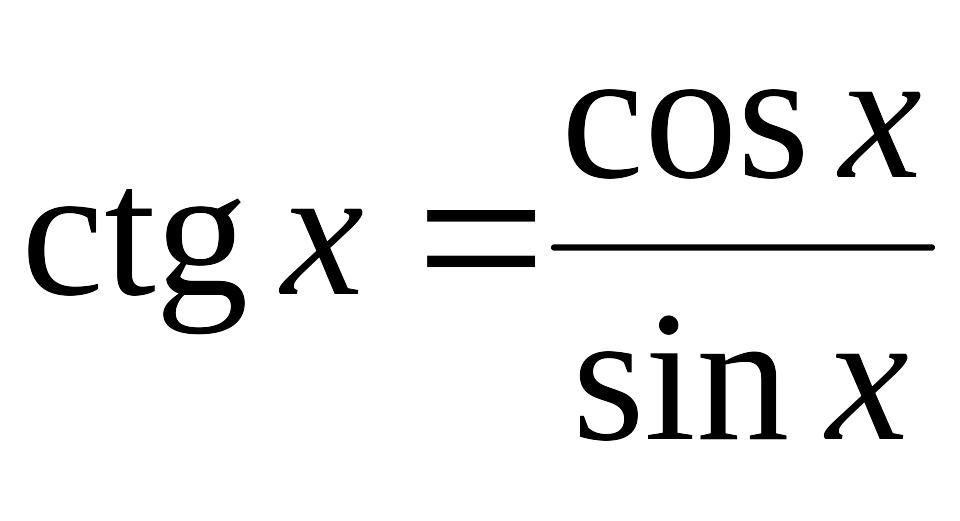Функции острых углов играют важную роль при решении многих математических и геодезических задач. Однако их использование ограничено пределами изменений острых углов от 0 до 90°. В геодезических построениях широко применяются косоугольные треугольники с пределами изменений углов свыше 90°, а в системе геодезического ориентирования используются углы (направления) с пределами изменений до 360°. Поэтому возникает необходимость распространения понятия тригонометрических функций на углы любой величины.

2.2.2 Тригонометрические функции произвольного угла

Тригонометрические функции угла любой величины определяют с помощью геодезического круга (рисунок 29) с двумя взаимно перпендикулярными диаметрами. За центр круга принимают точку стояния прибора или точку с известными координатами Р, за вертикальный диаметр SN геодезического круга – ось абсцисс данной точки (ось X). За горизонтальный диаметр WE геодезического круга принимают ось ординат (ось Y), за положительные направления осей – направления в сторону увеличения значений координат X и Y: для абсцисс – на север (вверх), для ординат – на восток (вправо).

За подвижный радиус РВ принимают направление (дирекционный угол) из данной точки на заданный предмет. Отсчет углов в геодезическом круге ведут от положительного (северного) направления оси абсцисс до направления на заданный предмет (подвижный радиус) по ходу часовой стрелки от 0 до 290°.

Четверти круга нумеруют в зависимости от направления подвижного радиуса: I четверть от 0 до 90°; II четверть от 90 до 180°; III четверть от 180 до 270°; IV четверть от 270 до 290° (на рисунке 29 двойными пунктирными линиями показано расположение подвижного радиуса во II, III и IV четвертях круга). На геодезическом круге производится построение тригонометрических .линий.

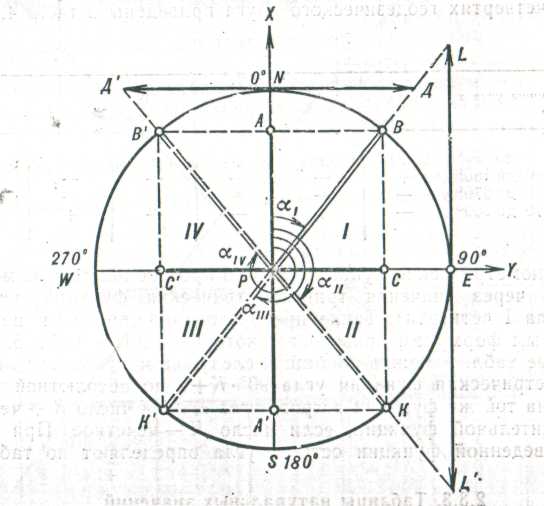
Рисунок 29 – Геодезический круг

Линией синуса называется проекция подвижного радиуса на ось ординат (на рисунке 29 отрезки РС и РС'),

Линией косинуса называется проекция подвижного радиуса: на ось абсцисс (на рисунке 29 отрезки РА и РА').

Линией тангенса называется отрезок касательной к геодезическому кругу в точке севера N от точки касания до пересечения с продолжением подвижного радиуса (на рисунке 29 отрезки NД и NД').

Линией котангенса называется отрезок касательной к геодезическому кругу в точке востока Е от точки касания до пересечения с продолжением подвижного радиуса (на рисунке 29 отрезки EL и EL').

Тригонометрическими функциями произвольного угла (угла любой величины) называются числовые значения взаимного отношения длин тригонометрических линий к длине подвижного радиуса геодезического круга. Так, синусом произвольного угла называется числовое значение отношения длины линии синуса (взятой со своим знаком) к длине подвижного радиуса геодезического круга (в I, II, III и IV четвертях):

; .

Косинусом произвольного угла называется числовое значение отношения длины линии косинуса (взятой со своим знаком) к длине подвижного радиуса геодезического круга:

; .

Знаки тригонометрических функций произвольного угла в различных четвертях геодезического круга приведены в таблице 4.

Таблица 4 – Знаки тригонометрических функций

Чет-верть	Величина угла αi	Sin αi	Cos αi	tg αi	ctg αi	sec αi	cosec αi
I II III IV	От 0о до 90о От 90о до 180о От 180о до 270о От 270о до 360о	+ + – –	+ – – +	+ – + –	+ – + –	+ – – +	+ + – –

Тригонометрические функции любого произвольного угла можно выразить через значения тригонометрических функций острого угла (угла I четверти). Такие преобразования проводят по так называемым формулам приведения, которые даны в таблице 5.

Таблица 5 – Формулы приведения

Данные таблицы 4 можно обобщить следующим правилом: любая тригонометрическая функция угла 90°∙К + α по абсолютной величине равна той же функции острого угла α, если число К – четное, и дополнительной функции, если число К – нечетное. При этом знак приведенной функции острого угла определяют по таблице 5.