Результаты измерений

Параметры	Номер измерения
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Емкость батареи С, мкФ
Частота собственных колебаний , Гц
(V1) Напряжение UC, В
(V2) Напряжение UL, В
(V3) Напряжение UR, В

L = ...............Гн; = ..................В.

Контрольные вопросы

1. В чем состоит резонанс напряжений в контуре?

2. Выведите формулу для амплитуды силы тока установившихся вынужденных колебаний в контуре.

3. Выведите формулу для сдвига фаз между силой тока в контуре и вынуждающей ЭДС.

4. Чему равна разность фаз между силой тока в контуре и вынуждающей ЭДС при резонансе?

5. Чему равна разность фаз напряжений на катушке индуктивности и на батарее конденсаторов?

Литература

1. Савельев И.В. Курс общей физики. Т. II. – М.: Наука, 2007.

2. Детлаф А.А., Яворский Б.М., Курс общей физики. – М.: Высшая школа, 2010.

Работа 77

РЕЗОНАНС ТОКОВ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Цель работы: изучение распределения токов в различных ветвях электрического контура при резонансной и близких к ней частотах.

Введение

Резонанс токов возникает при определенных условиях в электрическом контуре, содержащем параллельно включенные катушку индуктивности L и конденсатор емкостью C (рис.1). Активные сопротивления в ветвях обозначены R₀, R₁ и R₂. В контур включается источник тока, ЭДС которого зависит от времени по гармоническому закону .

С R₁

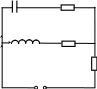
i₁ i₂ L R₂

i

R₀



Рис. 1

Резонанс токов сопровождается рядом интересных особенностей, которые можно установить при расчете токов в схеме рис. 1 и проверить экспериментально. Предполагая, что величина циклической частоты вынуждающей ЭДС  и размеры электрического контура обеспечивают квазистационарность токов, применим правило Кирхгофа для выяснения характера установившихся вынужденных колебаний тока в этом контуре. Для мгновенных значений токов, сходящихся в узле, используя первое правило Кирхгофа можно написать равенство

i = i₁ + i₂ . (1)

При составлении уравнений для контуров воспользуемся уравнением (2) работы 76, теоретическую часть которой необходимо изучить, приступая к подготовке данной лабораторной работы. Запишем это уравнение

. (2)

Нетрудно видеть, что уравнение для контура, содержащего С, R₁, R₀ и  (см. рис.1), получается из уравнения (2), если принять L=0, R₀=0 и R=R₁:

Используя решение уравнения (2) в работе 76, получим для силы тока i₁ следующее выражение:

.

Амплитуда силы тока i₀₁ и сдвиг по фазе между током и вынуждающей ЭДС ₁ имеют вид

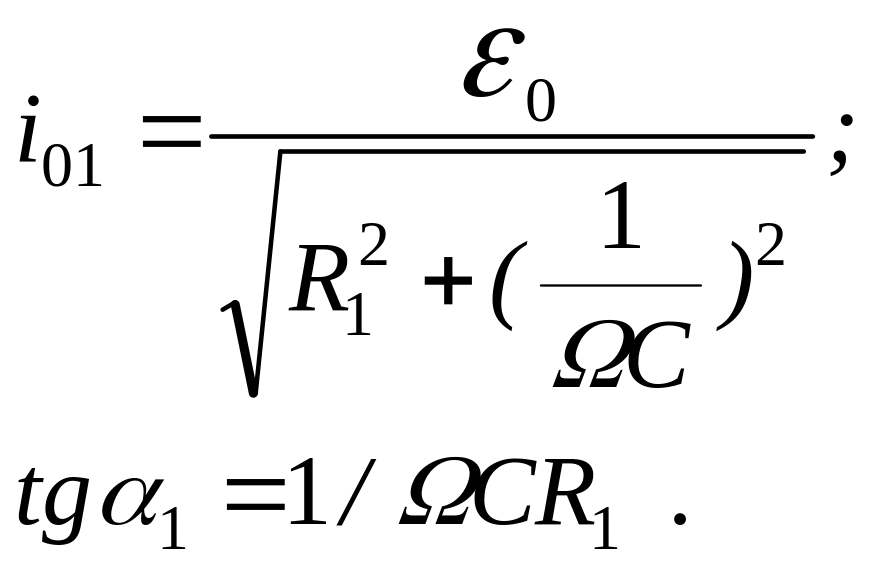(3)

Для контура, содержащего L, R₂, R₀ и , из уравнения (2) в предположении, что , R₀=0 и R=R₂, получим уравнение

.

Из этого уравнения следует такое выражение для силы тока i₂:

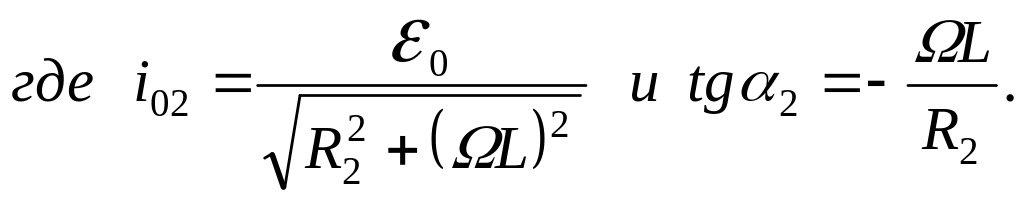(4)

Так как циклическая частота  токов i₁ и i₂ при установившихся вынужденных колебаниях одинакова, то согласно формуле (1) силу тока i можно представить в виде

(5)

Как видно из формул (3-5), сила токов в ветвях и фазовые соотношения между ними и ЭДС определяются параметрами L, C, ₀, , R₁ и R₂.

Известно, что наиболее выразительно явление резонанса проявляется при отсутствии активного сопротивления. Допустим для этого предельного случая, что R₁=R₂=0. Тогда

При этом амплитудное значение тока в неразветвленной части цепи оказывается наименьшим:

а токи в ветвях (i₁ и i₂) изменяются противофазно. Из последнего равенства вытекает условие, при котором ток в неразветвленной части цепи обращается в нуль. Для этого необходимо, чтобы частота вынуждающей ЭДС стала равной собственной частоте колебаний идеального контура (содержащего индуктивность и емкость).

Итак, при выполнении условий R₀=R₁=R₂=0 и ток в неразветвленной части цепи обращается в нуль, а в ветвях, содержащих индуктивность и емкость, амплитудные значения токов становятся одинаковыми и могут быть большими по величине. Это явление именуется резонансом токов.

Соотношение между токами i₁ и i₂ можно изобразить наглядно с помощью векторной диаграммы токов. При построении диаграммы вектора токов необходимо откладывать относительно оси напряжений, в качестве которой выберем горизонтальную ось (рис. 2).

Ток в индуктивности отстает от напряжений на /2 и потому изображается вектором, повернутым относительно оси напряжений против часовой стрелки на угол /2. Ток в емкости опережает напряжение на /2, соответственно он повернут относительно оси напряжений по часовой стрелке на угол /2. При резонансе длины векторов обоих токов одинаковы, а результирующий ток равен нулю.



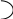Ось напряжений



Рис. 2

Однако в реальном контуре в полной мере выполнить указанные условия практически невозможно. Поэтому в данной лабораторной работе будет наблюдаться резкое уменьшение тока в неразветвленной части цепи, сопровождающееся выравниванием величин токов в ветвях с катушкой индуктивности и батареи конденсаторов, когда собственная частота колебаний контура будет приближаться к фиксированной частоте электродвижущей силы .