ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ»

Кафедра “Физика”

С.И. ИЛЬИН

С.В. МУХИН

Резонанс напряжений в колебательном контуре

Методические указания

к лабораторным работам

по дисциплине

«ФИЗИКА»

РАБОТЫ 76, 77

Москва – 2012

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ»

Кафедра “Физика”

С.И. ИЛЬИН

С.В. МУХИН

Резонанс напряжений в колебательном контуре

Рекомендовано редакционно-издательским

советом университета в качестве

методических указаний для студентов 1 и 2 курса

всех специальностей

Москва – 2012

УДК 537.86

И46

Ильин С.И., Мухин С.В. Резонанс напряжений в колебательном контуре. Методические указания к лабораторным работам по дисциплине «Физика». Работы 76, 77. – М.: МИИТ, 2012. – 20 с.

Методические указания к лабораторным работам по физике № 76 и № 77 соответствуют программе и учебным планам по курсу общей физики (раздел «Колебания и волны») и предназначены для всех специальностей институтов ИУИТ, ИТТСУ, ИЭФ.

 МИИТ, 2012

Работа 76

РЕЗОНАНС НАПРЯЖЕНИЙ

В колебательном контуре

Цель работы: изучение распределения напряжений на разных участках цепи электрического контура при резонансе и вблизи него.

Введение

Резонанс напряжений возникает в электрическом контуре, содержащем последовательно соединенные катушку индуктивности L, конденсатор с электрической емкостью С и активное сопротивление R (рис.1).

L

С R



Рис. 1

Будем считать, что источник тока, включенный в контур, имеет электродвижущую силу , изменяющуюся со временем по синусоидальному закону:

,

где _о – амплитуда ЭДС;  – циклическая частота ЭДС.

Если ограничиться случаем квазистационарных токов, то к мгновенным значениям силы тока i, ЭДС и напряжения на обкладках конденсатора U_c может быть применено 2-е правило Кирхгофа (в любом замкнутом контуре алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС):

iR + U_c = , (1)

где  – алгебраическая сумма ЭДС источника тока и ЭДС самоиндукции _с на участке с сосредоточенной индуктивностью L.

Выразим в этом уравнении силу тока в контуре, напряжение на конденсаторе и ЭДС самоиндукции через переменный заряд на обкладках конденсатора q:

После подстановки получим неоднородное линейное дифференциальное уравнение второго порядка – уравнение вынужденных электрических колебаний.

. (2)

Она определяет как общий характер, так и все особенности вынужденных колебаний в контуре. Нас будут интересовать, в частности, зависимости от времени силы тока и напряжений (на разных участках цепи) и сдвиг по фазе между ними.

Решение уравнения (2) состоит из суммы общего решения этого уравнения без правой части (однородного) и частного решения неоднородного уравнения (2). Решение однородного уравнения является затухающим электрическим колебанием. Если произведение 1, то этим колебанием можно пренебречь. Поэтому решение установившихся электрических колебаний будем искать в виде

(3)

Определим, при каких значениях амплитуды тока i₀ и сдвига фаз  между силой тока и вынуждающей ЭДС зависимость i(t) в виде (3) обращает уравнение (2) в тождество. Из формулы (3) следует, что

;

Подставив эти выражения в уравнение (2), получим:

(5)

Используя соотношения

и , (6)

перепишем уравнение (5) в виде

(7)

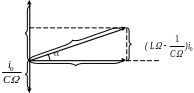
Полученное соотношение между переменными токами и напряжениями делается особенно наглядным, если изобразить его с помощью векторов. (Совокупность векторов напряжений или токов образует векторную диаграмму данной цепи). Рассмотрим цепь, используемую в данной работе (рис. 1). При подаче на концы этой цепи напряжения частотой  в ней возникает переменный ток той же частоты, амплитуда i₀ и фаза  которого определяются параметрами цепи. Выберем произвольное направление, которое назовем осью токов (рис. 2).

₀

Ось токов

Ri₀

Рис. 2

Этот ток вызовет на активном сопротивлении напряжение , амплитуда которого равна Ri₀, а фаза совпадает с фазой тока (второе слагаемое в левой части уравнения (7)). Поэтому на векторной диаграмме вектор, изображающий , нужно отложить по оси токов. Напряжение на индуктивности (с амплитудой Li₀) опережает ток по фазе на /2; поэтому вектор, изображающий , должен быть повернут относительно оси токов на угол /2 против часовой стрелки. Наконец, напряжение на емкости (имеющее амплитуду ) отстает от тока по фазе на /2; следовательно, вектор, изображающий , должен быть повернут относительно оси токов на угол /2 по часовой стрелке.

Напряжения , и в сумме должны быть равны приложенному к цепи напряжению ₀. Поэтому, сложив векторы, изображающие , и , мы получим вектор, изображающий  (на рис.2 изображены амплитудные значения величин напряжений). Из векторной диаграммы легко получить соотношения (8) и (9), определяющие разность фаз между силой тока в цепи и вынуждающей ЭДС и амплитуду силы тока в цепи.

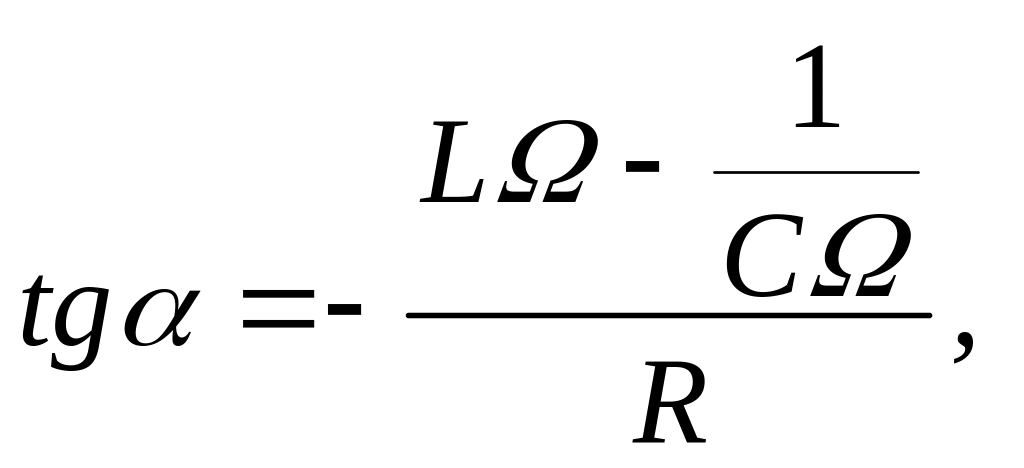(8)

и формулу для амплитуды силы тока

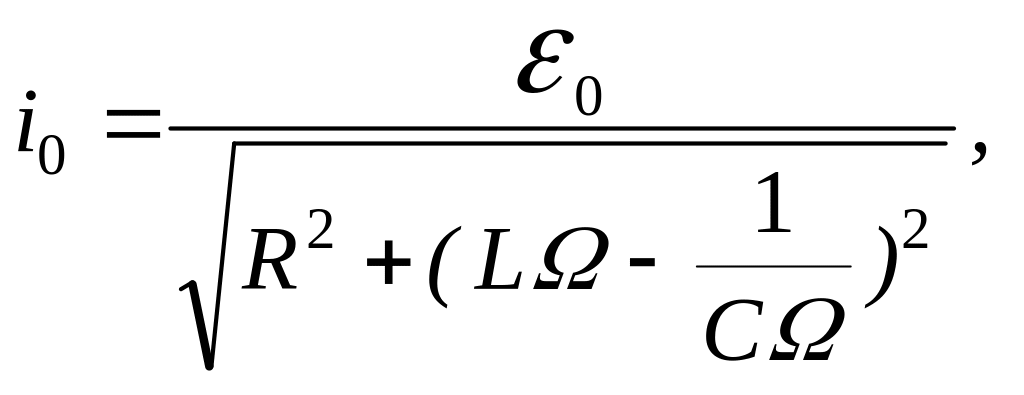(9)

где – полное сопротивление цепи переменного тока; R – активное (омическое) сопротивление; – реактивное сопротивление.

Как видно из уравнений (8) и (9), амплитуда силы тока и сдвиг фаз зависят не только от параметров контура, но и от частоты вынуждающей ЭДС. При этом легко определить частоту, при которой реактивное сопротивление становится равным нулю:

Эта частота _p, как видно, совпадает с частотой собственных незатухающих колебаний в контуре и называется резонансной, так как ей соответствует максимальное значение амплитуды силы тока

и нулевое значение сдвига фаз между током и вынуждающей ЭДС. Явление резкого возрастания амплитуды силы тока и сближения фаз колебаний тока и вынуждающей ЭДС при приближении частоты вынуждающей ЭДС к собственной частоте колебаний в контуре называется резонансом. Он сопровождается не только отмеченными, но и рядом других характерных особенностей. Рассмотрим, в частности, напряжение при резонансной частоте сначала на концах катушки индуктивности, а затем между обкладками конденсатора:

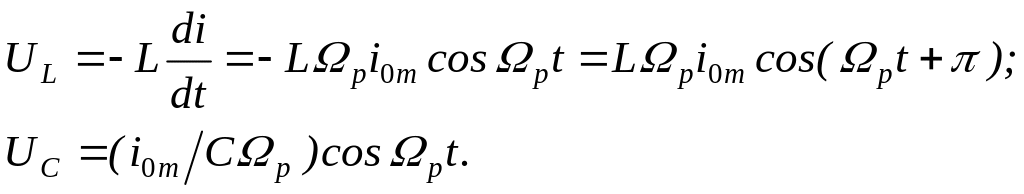
Сравнение этих двух напряжений показывает, что амплитуды их при резонансе совпадают, а фазы колебаний противоположны. Значит, в условиях резонанса , а напряжение на активном сопротивлении должно быть максимальным. Этот вид резонанса и называют резонансом напряжений.

Векторная диаграмма для случая резонанса напряжений показана на рис. 3.

₀ = Ri₀ ось токов

Рис. 3

Резонансная частота для заряда q и напряжения равна:

В данной работе должны быть экспериментально изучены отмеченные выше особенности распределения напряжений на разных участках колебательного контура при резонансе и при подходе к нему.