- •Методические указания к выполнению лабораторных работ
- •Лабораторная работа №1 «Введение в элементы языка лисп»
- •Работа в среде разработки.
- •Практические рекомендации:
- •Лабораторная работа №2 « Способы и методы хранения графической информации»
- •Основные особенности наиболее распространенных графических форматов
- •Цветовая модель rgb
- •Цветовая модель cmyk
- •Цветовые модели hsb и hsl
- •Пример программы работы с графическим файлом
- •Контрольные вопросы
- •Лабораторная работа №3 «Оформление чертежа в автоматизированной системе acad»
- •Лабораторная работа №4 «Выполнение позиционных задач в автоматизированной системе»
- •Изображение объектов трехмерного пространства. Метод проекций.
- •Ортогональные проекции.
- •Лабораторная работа №5 «Выполнение метрических задач в автоматизированной системе»
- •Способ прямоугольного треугольника
- •Способ замены плоскостей проекций
- •Лабораторная работа №6 «Выполнение пересечения фигур в автоматизированной системе»
- •Пересечение поверхностей
- •Лабораторная работа №7 «Выполнение разъемных и не разъемных соединений с использованием автоматизированной системы »
- •«Выполнение шпилечного соединения с использованием автоматизированной системы»
- •Лабораторная работа №9 «Эскиз простой детали»
- •Лабораторная работа №10 «Выполнение каркасной модели помещения с элементами инфраструктуры с использованием автоматизированной систем»
- •Несоблюдение стандарта преследуется по закону
- •Исполнение 1
- •Исполнение 2
Несоблюдение стандарта преследуется по закону
1. Настоящий стандарт распространяется на шпильки с номинальным диаметром резьбы от 2 до 48 мм, изготовляемые с крупным шагом резьбы на гаечном и ввинчиваемом концах, с мелким шагом резьбы на гаечном и ввинчиваемом концах, с мелким шагом резьбы на ввинчиваемом конце и крупным шагом резьбы на гаечном конце, с крупным шагом резьбы на ввинчиваемом конце и мелким шагом резьбы на гаечном конце.
(Измененная редакция, Изм. №4)
2. Конструкция и размеры шпилек должны соответствовать указанным на чертеже и в табл. 1, 2.
Исполнение 1

Исполнение 2
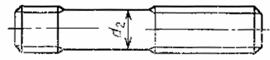
d2 приблизительно равен среднему диаметру резьбы
Примечание. (Исключено, Изм. №4)
Таблица 1
мм
Номинальный диаметр резьбы d |
2 |
2,5 |
3 |
4 |
5 |
6 |
8 |
10 |
12 |
(14) |
16 |
(18) |
20 |
(22) |
24 |
(27) |
30 |
36 |
42 |
48 |
|||||||||
Шаг Р: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
крупный |
0,4 |
0,45 |
0,5 |
0,7 |
0,8 |
1 |
1,25 |
1,5 |
1,75 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
|||||||||||||
мелкий |
- |
- |
- |
- |
- |
- |
1 |
1,25 |
1,5 |
2 |
3 |
||||||||||||||||||
Диаметр стержня d1 |
2 |
2,5 |
3 |
4 |
5 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
27 |
30 |
36 |
42 |
48 |
|||||||||
Длина ввинчиваемого резьбового конца b1 |
3 |
4 |
5 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
27 |
30 |
36 |
42 |
48 |
|||||||||||
Примечание. Размеры, заключенные в скобки, применять не рекомендуется.
(Измененная редакция, Изм. № 4)
Таблица 2
мм
Длина шпильки l |
Длина резьбы гаечного конца b при номинальном диаметре резьбы d |
|||||||||||||||||||
2 |
2,5 |
3 |
4 |
5 |
6 |
8 |
10 |
12 |
(14) |
16 |
(18) |
20 |
(22) |
24 |
(27) |
30 |
36 |
42 |
48 |
|
10 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
12 |
10 |
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
14 |
10 |
11 |
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
16 |
10 |
11 |
12 |
|
|
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
(18) |
10 |
11 |
12 |
14 |
|
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
20 |
10 |
11 |
12 |
14 |
16 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
(22) |
10 |
11 |
12 |
14 |
16 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
25 |
10 |
11 |
12 |
14 |
16 |
18 |
|
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
(28) |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
30 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
(32) |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
35 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
|
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
(38) |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
40 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
|
|
|
|
- |
- |
- |
- |
- |
- |
- |
(42) |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
|
|
|
|
- |
- |
- |
- |
- |
- |
- |
45 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
|
|
|
|
|
- |
- |
- |
- |
- |
(48) |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
|
|
|
|
- |
- |
- |
- |
- |
50 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
|
|
|
|
- |
- |
- |
- |
- |
55 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
|
|
|
|
- |
- |
- |
- |
60 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
|
|
|
|
- |
- |
- |
65 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
|
|
|
- |
- |
- |
70 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
|
|
|
- |
- |
75 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
|
|
- |
- |
80 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
|
|
|
|
85 |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
|
|
|
90 |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
|
|
|
(95) |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
78 |
|
|
100 |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
78 |
|
|
(105) |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
78 |
|
|
110 |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
78 |
90 |
|
(115) |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
78 |
90 |
|
120 |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
78 |
90 |
|
130 |
- |
17 |
18 |
20 |
22 |
24 |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
140 |
- |
17 |
18 |
20 |
22 |
24 |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
150 |
- |
17 |
18 |
20 |
22 |
24 |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
81 |
96 |
108 |
160 |
- |
17 |
18 |
20 |
22 |
24 |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
170 |
- |
- |
- |
- |
- |
- |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
180 |
- |
- |
- |
- |
- |
- |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
190 |
- |
- |
- |
- |
- |
- |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
200 |
- |
- |
- |
- |
- |
- |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
220 |
- |
- |
- |
- |
- |
- |
- |
- |
49 |
53 |
57 |
61 |
65 |
69 |
73 |
79 |
85 |
97 |
109 |
121 |
240 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
65 |
69 |
73 |
79 |
85 |
97 |
109 |
121 |
260 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
79 |
85 |
97 |
109 |
121 |
280 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
97 |
109 |
121 |
300 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
97 |
109 |
121 |
Примечания:
1. Размеры, заключенные в скобки, применять не рекомендуется.
2. Знаком отмечены шпильки с длиной гаечного конца b=l-0,5d-2Р.
Таблица 1
мм
Номинальный диаметр резьбы d |
2 |
2,5 |
3 |
4 |
5 |
6 |
8 |
10 |
12 |
(14) |
16 |
(18) |
20 |
(22) |
24 |
(27) |
30 |
36 |
42 |
48 |
|||||||||
Шаг Р: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
крупный |
0,4 |
0,45 |
0,5 |
0,7 |
0,8 |
1 |
1,25 |
1,5 |
1,75 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
|||||||||||||
мелкий |
- |
- |
- |
- |
- |
- |
1 |
1,25 |
1,5 |
2 |
3 |
||||||||||||||||||
Диаметр стержня d1 |
2 |
2,5 |
3 |
4 |
5 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
27 |
30 |
36 |
42 |
48 |
|||||||||
Длина ввинчиваемого резьбового конца b1 |
3 |
4 |
5 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
27 |
30 |
36 |
42 |
48 |
|||||||||||
Примечание. Размеры, заключенные в скобки, применять не рекомендуется.
(Измененная редакция, Изм. № 4)
Таблица 2
мм
Длина шпильки l |
Длина резьбы гаечного конца b при номинальном диаметре резьбы d |
|||||||||||||||||||
2 |
2,5 |
3 |
4 |
5 |
6 |
8 |
10 |
12 |
(14) |
16 |
(18) |
20 |
(22) |
24 |
(27) |
30 |
36 |
42 |
48 |
|
10 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
12 |
10 |
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
14 |
10 |
11 |
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
16 |
10 |
11 |
12 |
|
|
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
(18) |
10 |
11 |
12 |
14 |
|
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
20 |
10 |
11 |
12 |
14 |
16 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
(22) |
10 |
11 |
12 |
14 |
16 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
25 |
10 |
11 |
12 |
14 |
16 |
18 |
|
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
(28) |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
30 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
(32) |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
35 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
|
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
(38) |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
40 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
|
|
|
|
- |
- |
- |
- |
- |
- |
- |
(42) |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
|
|
|
|
- |
- |
- |
- |
- |
- |
- |
45 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
|
|
|
|
|
- |
- |
- |
- |
- |
(48) |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
|
|
|
|
- |
- |
- |
- |
- |
50 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
|
|
|
|
- |
- |
- |
- |
- |
55 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
|
|
|
|
- |
- |
- |
- |
60 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
|
|
|
|
- |
- |
- |
65 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
|
|
|
- |
- |
- |
70 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
|
|
|
- |
- |
75 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
|
|
- |
- |
80 |
10 |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
|
|
|
|
85 |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
|
|
|
90 |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
|
|
|
(95) |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
78 |
|
|
100 |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
78 |
|
|
(105) |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
78 |
|
|
110 |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
78 |
90 |
|
(115) |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
78 |
90 |
|
120 |
- |
11 |
12 |
14 |
16 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
54 |
60 |
66 |
78 |
90 |
|
130 |
- |
17 |
18 |
20 |
22 |
24 |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
140 |
- |
17 |
18 |
20 |
22 |
24 |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
150 |
- |
17 |
18 |
20 |
22 |
24 |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
81 |
96 |
108 |
160 |
- |
17 |
18 |
20 |
22 |
24 |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
170 |
- |
- |
- |
- |
- |
- |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
180 |
- |
- |
- |
- |
- |
- |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
190 |
- |
- |
- |
- |
- |
- |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
200 |
- |
- |
- |
- |
- |
- |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
66 |
72 |
84 |
96 |
108 |
220 |
- |
- |
- |
- |
- |
- |
- |
- |
49 |
53 |
57 |
61 |
65 |
69 |
73 |
79 |
85 |
97 |
109 |
121 |
240 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
65 |
69 |
73 |
79 |
85 |
97 |
109 |
121 |
260 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
79 |
85 |
97 |
109 |
121 |
280 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
97 |
109 |
121 |
300 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
97 |
109 |
121 |
Примечания:
1. Размеры, заключенные в скобки, применять не рекомендуется.

Пример реализации алгоритма Хаффмана на языке Delphi
unit CHuffman;
interface
uses
SysUtils, Classes, Dialogs;
const
ALPHABETSIZE = 256;
type
TTree = class;
THuffman = class;
TTree = class(TObject)
private
fchild0 : TTree; // потомки "0" и "1"
fchild1 : TTree;
fleaf : Boolean; // признак листового дерева
fcharacter : Integer; // входной символ
fweight : Integer; // вес этого символа
public
procedure Tree(character, weight : integer; leaf : boolean);
procedure traverse(code : string; h : THuffman);
property child0 : TTree read fchild0 write fchild0;
property child1 : TTree read fchild1 write fchild1;
property leaf : Boolean read fleaf write fleaf;
property character : Integer read fcharacter write fcharacter;
property weight : Integer read fweight write fweight;
end;
THuffman = class(TObject)
private
// поля :)
fweights : array [0..ALPHABETSIZE-1] of Integer;// веса символов
fcode : array [0..ALPHABETSIZE-1] of String;// коды Хаффмана
ftree : array [0..ALPHABETSIZE-1] of TTree;// рабочий массив деревьев
// методы доступа к массиву :)
function GetCodeValue(Index: Integer): String;
function GetTreeValue(Index: Integer): TTree;
function GetWeightValue(Index: Integer): Integer;
procedure SetCodeValue(Index: Integer; const Value: String);
procedure SetTreeValue(Index: Integer; const Value: TTree);
procedure SetWeightValue(Index: Integer; const Value: Integer);
public
// методы :)
procedure makeCode;
procedure growTree(var data : array of Integer);
function getLowestTree(used : integer) : integer;
function coder(var data : array of integer) : string;
function decoder(data : string) : string;
// свойства :)
property weights[Index: Integer] : Integer read GetWeightValue write SetWeightValue;
property code[Index: Integer] : String read GetCodeValue write SetCodeValue;
property tree[Index: Integer] : TTree read GetTreeValue write SetTreeValue;
end;
var
Huffman : THuffman;
implementation
{ TTree }
procedure TTree.Tree(character, weight: integer; leaf: boolean);
begin
fleaf := leaf;
fcharacter := character;
fweight := weight;
end;
(* Обход дерева с генерацией кодов
1. "Распечатать" листовое дерево и записать код Хаффмана в массив
2. Рекурсивно обойти левое поддерево (с генерированием кода).
3. Рекурсивно обойти правое поддерево. *)
procedure TTree.traverse(code: String; h: THuffman);
begin
if leaf then
begin
h.code[Ord(character)] := code;
ShowMessage('Символ: ' + Chr(character) +' '+'Вес: '+IntToStr(weight) +' '+'Двоичный код: '+ code);
end;
if child0 <> nil then child0.traverse(code + '0', h);
if child1 <> nil then child1.traverse(code + '1', h);
end;
{ THuffman }
(* ищем самое "легкое" дерево *)
function THuffman.getLowestTree(used: integer): integer;
var
min, i : Integer;
begin
min := 0;
for i:=1 to used-1 do if tree[i].weight < tree[min].weight then min := i;
Result := min;
end;
(* кодирует данные строкой из 1 и 0 *)
function THuffman.coder(var data: array of Integer): String;
var
str : String;
i : Integer;
begin
str := '';
for i:=0 to High(data) do str := str + code[data[i]];
Result := str;
end;
function THuffman.decoder(data : string): string;
var
str : String;
c : Integer;
begin
str := '';
while(length(data) > 0) do
begin
for c:=0 to ALPHABETSIZE-1 do
if (weights[c] > 0) AND (code[c] = copy(data, 1, length(code[c]))) then
begin
data := copy(data, length(code[c])+1, length(data));
str := str + chr(c) + ' - ' + code[c] + #13;
end;
end;
Result := str;
end;
(* растим дерево *)
procedure THuffman.growTree(var data: array of Integer);
var
i, c, w, min, used, weight0 : Integer;
temp : TTree;
begin
for i:=0 to ALPHABETSIZE-1 do weights[i] := 0;
for i:=0 to High(data) do weights[data[i]] := weights[data[i]] + 1; // считаем веса символов
// заполняем массив из "листовых" деревьев
// с использованными символами
used := 0;
for c:=0 to ALPHABETSIZE-1 do
begin
w := weights[c];
if w <> 0 then
begin
inc(used);
tree[used-1] := TTree.Create;
tree[used-1].Tree(c, w, true);
end;
end;
while used > 1 do // парами сливаем легкие ветки
begin
min := getLowestTree(used); // ищем 1 ветку
weight0 := tree[min].weight;
temp := TTree.Create; // создаем новое дерево
temp.child0 := tree[min]; // и прививаем 1 ветку
dec(used);
tree[min] := tree[used]; // на место 1 ветки кладем
// последнее дерево в списке
min := getLowestTree(used); // ищем 2 ветку и
temp.child1 := tree[min]; // прививаем ее к нов.дер.
temp.weight := weight0 + tree[min].weight; // считаем вес нов.дер.
tree[min] := temp; // нов.дер. кладем на место 2 ветки
end; // все! осталось 1 дерево Хаффмана
end;
(* запускаем вычисление кодов Хаффмана *)
procedure THuffman.makeCode;
begin
tree[0].traverse('', self);
end;
function THuffman.GetCodeValue(Index: Integer): String;
begin
Result := fcode[Index];
end;
function THuffman.GetTreeValue(Index: Integer): TTree;
begin
Result := ftree[Index];
end;
function THuffman.GetWeightValue(Index: Integer): Integer;
begin
Result := fweights[Index];
end;
procedure THuffman.SetCodeValue(Index: Integer; const Value: String);
begin
fcode[Index] := Value;
end;
procedure THuffman.SetTreeValue(Index: Integer; const Value: TTree);
begin
ftree[Index] := Value;
end;
procedure THuffman.SetWeightValue(Index: Integer; const Value: Integer);
begin
fweights[Index] := Value;
end;
end.
Результат работы для строки «to be or not to be?». Выводятся: символ, его вес и двоичный код. Далее закодированная строка и результат декодирования.
e 2 000
? 1 0010
n 1 0011
o 4 01
5 10
t 3 110
r 1 1110
b 2 1111
11001101111000100111101000110111010110011011110000010
to be or not to be?
-----------------------------------------------------------------------
110 01 10 1111 000 10 01 1110 10 0011 01 110 10 110 01 10 1111 000 0010
t o b e o r n o t t o b e ?
Итого:
53 бита
19 знаков (с пробелами)
2,79 бит/знак
Алгоритм JPEG
В алгоритме JPEG исходное изображение представляется двумерной матрицей размера N*N, элементами которой являются цвет или яркость пиксела. Упаковка значений матрицы выполняется за три этапа.
Дискретное косинус преобразование
Этап Квантования
Этап Вторичного Сжатия
Высокая эффективность сжатия, которую дает этот алгоритм, основана на том факте, что в матрице частотных коэффициентов, образующейся из исходной матрицы после дискретного косинусного преобразования, низкочастотные компоненты расположены ближе к левому верхнему углу, а высокочастотные - внизу справа. Это важно потому, что большинство графических образов на экране компьютера состоит из низкочастотной информации, так что высокочастотные компоненты матрицы можно безболезненно выбросить.“Выбрасывание” выполняется путем округления частотных коэффициентов. После округления отличные от нуля значения низкочастотных компонент остаются, главным образом, в левом верхнем углу матрицы. Округленная матрица значений кодируется с учетом повторов нулей. В результате графический образ сжимается более чем на 90% , теряя очень немного в качестве изображения только на этапе округления.
Дискретное косинус преобразование
Основным этапом работы алгоритма является дискретное косинусное преобразование (ДКП), представляющее собой разновидность преобразования Фурье. Оно позволяет переходить от пространственного представления изображения к его спектральному представлению и обратно. Что нужно сделать на первом этапе первом этапе ? Следует создать ДКП матрицу, используя такую формулу :
DCT = 1/sqr(N), если i=0
ij
DCT = sqr(2/N)*cos[(2j+1)*i*3.14/2N], если i > 0
ij
N = 8, 0 < i < 7 , 0 < j < 7
в результате имеем:
|.353553 .353553 .353553 .353553 .353553 .353553 .353553 .353553|
|.490393 .415818 .277992 .097887 -.097106 -.277329 -.415375 -.490246|
|.461978 .191618 -.190882 -.461673 -.462282 -.192353 .190145 .461366|
DCT = |.414818 -.097106 -.490246 -.278653 .276667 .490710 .099448 -.414486|
|.353694 -.353131 -.354256 .352567 .354819 -.352001 -.355378 .351435|
|.277992 -.490246 .096324 .416700 -.414486 -.100228 .491013 -.274673|
|.191618 -.462282 .461366 -.189409 -.193822 .463187 -.460440 .187195|
|.097887 -.278653 .416700 -.490862 .489771 -.413593 .274008 -.092414|
например, нам нужно сжать следующий фрагмент изображения:
| 95 88 88 87 95 88 95 95|
|143 144 151 151 153 170 183 181|
|153 151 162 166 162 151 126 117|
IMG = |143 144 133 130 143 153 159 175|
|123 112 116 130 143 147 162 189|
|133 151 162 166 170 188 166 128|
|160 168 166 159 135 101 93 98|
|154 155 153 144 126 106 118 133|
|-33 -40 -40 -41 -33 -40 -33 -33|
| 15 16 23 23 25 42 55 53|
| 25 23 34 38 34 23 -2 -11|
IMG = | 15 16 5 2 15 25 31 47|
| -5 -16 -12 2 15 19 34 61|
| 5 23 34 38 42 60 38 0|
| 32 40 38 31 7 -27 -35 -30|
| 26 27 25 16 -2 -22 -10 5|
T
вот формула, по которой производится ДКП: RES*IMG*DCT
T
для начала нужно посчитать промежуточную матрицу: TMP = IMG*DCT
|-103 -3 1 2 4 0 -1 5|
| 89 -40 12 -2 -7 5 1 0|
| 57 31 -30 6 2 0 5 0|
TMP = | 55 -28 24 1 0 -8 0 0|
| 32 -60 18 -1 14 0 -8 1|
| 84 -11 -37 17 -24 4 0 -4|
| 19 81 -16 -20 8 -3 4 0|
| 22 40 11 -22 8 0 -3 2|
затем умножаем ее на ДКП матрицу: RES = TMP*DCT
| 91 3 -5 -6 2 0 1|
|-38 -57 9 17 -2 2 2|
|-80 58 0 -18 4 3 4|
RES = |-52 -36 -11 13 -9 3 0|
|-86 -40 44 -7 17 -6 4|
|-62 64 -13 -1 3 -8 0|
|-16 14 -35 17 -11 2 -1|
|-53 32 -9 -8 22 0 2|
Этап Квантования
На этом этапе мы посчитаем матрицу квантования, используя этот псевдо код:
for i:=0 to 8 do
for j:=0 to 8 do
Q[i,j] = 1+((1+i+j)*q);
где q - это коэффициент качества, от него зависит степень потери качества сжатого изображения для q = 2 имеем матрицу квантования:
| 3 5 7 9 11 13 15 17|
| 5 7 9 11 13 15 17 19|
| 7 9 11 13 15 17 19 21|
Q = | 9 11 13 15 17 19 21 23|
|11 13 15 17 19 21 23 25|
|13 15 17 19 21 23 25 27|
|15 17 19 21 23 25 27 29|
|17 19 21 23 25 27 29 31|
теперь нужно каждое число в матрице квантования разделить на число в соответствущей позиции в матрице RES, в результате получим:
| 30 0 0 0 0 0 0 0|
| -7 8 1 1 0 0 0 0|
|-11 6 0 1 0 0 0 0|
A = | -5 -3 0 0 0 0 0 0|
| -7 -3 2 0 0 0 0 0|
| -4 4 0 0 0 0 0 0|
| -1 0 1 0 0 0 0 0|
| -3 1 0 0 0 0 0 0|
как вы видите здесь имеется довольно много нулей, мы получим наиболее длинную последовательность нулей, если будем использовать следущий алгоритм:
+----+----+----+----+----+----+----+----+
| 1 | 2 | 6 | 7 | 15 | 16 | 28 | 29 |
+----+----+----+----+----+----+----+----+
| 3 | 5 | 8 | 14 | 17 | 27 | 30 | 43 |
+----+----+----+----+----+----+----+----+
| 4 | 9 | 13 | 18 | 26 | 31 | 42 | 44 |
+----+----+----+----+----+----+----+----+
| 10 | 12 | 19 | 25 | 32 | 41 | 45 | 54 |
+----+----+----+----+----+----+----+----+
| 11 | 20 | 24 | 33 | 40 | 46 | 53 | 55 |
+----+----+----+----+----+----+----+----+
| 21 | 23 | 34 | 39 | 47 | 52 | 56 | 61 |
+----+----+----+----+----+----+----+----+
| 22 | 35 | 38 | 48 | 51 | 57 | 60 | 62 |
+----+----+----+----+----+----+----+----+
| 36 | 37 | 49 | 50 | 58 | 59 | 63 | 64 |
+----+----+----+----+----+----+----+----+
итак у нас получилась последовательность:
30 0 -7 -11 8 0 0 1 6 -5 -7 -3 0 1 0 0 0 1 0 -3 -4 -1 4 2 0 0 0 0
0 0 0 0 0 0 0 -3 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Этап Вторичного Сжатия.
Самым распространенным методом вторичного сжатия является метод Хаффмана и его разновидности.
Метод Хаффмана.
Сжатие Хаффмана - статистический метод сжатия, который уменьшает среднюю длину кодового слова для символов алфавита. Код Хаффмана является примером кода, оптимального в случае, когда все вероятности появления символов в сообщении - целые отри- цательные степени двойки. Код Хаффмана может быть построен по следующему алгоритму:
Выписываем в ряд все символы алфавита в порядке возрастания или убывания вероятности их появления в тексте;
Последовательно объединяем два символа с наименьшими вероятностями появления в новый составной символ, вероятность появления которого полагается равной сумме вероятностей составляющих его символов. В конце концов, мы построим дерево, каждый узел которого имеет суммарную вероятность всех узлов, находящихся ниже него;
Прослеживаем путь к каждому листу дерева помечая направление к каждому узлу (например, направо - 1, налево - 0).
Поясним создание дерева с использованием иллюстраций :
A B C D E
10 5 8 13 10
B C A E D
5 8 10 10 13
A E BC D
10 10 13 13
BC D AE
13 13 20
AE BCD
20 26
AEBCD
46
Таким образом, построено дерево
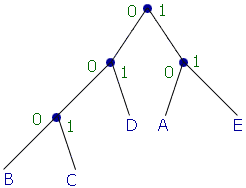
Теперь, если в тексте встречается, например, символ "d", то вместо того, чтобы выделять этому символу байт, после