5. Формы представления информации в компьютере.

5.1. Кодирование в компьютерах числовой информации.

Системы счисления и переводы чисел из одной системы счисления в другую.

Системой счисления называется способ представления (кодирования)

чисел посредством некоторого множества символов, называемых

цифрами.

В любой системе счисления число может быть записано в виде некоторой строчки символов:

а_nа_n-1а_n-2…а₁a₀,a_-1a_-2a_-3…a_-m

где a_i – символы из некоторого множества {a},

, – запятая, отделяющая целую часть числа от дробной части.

Системы счисления делятся на два больших класса:

а) позиционные системы счисления;

б) непозиционные системы счисления.

Система счисления называется позиционной, если значение символа

(цифры) определяется не только видом, но и местом расположения

(позицией) в представлении числа.

Непозиционными называются системы счисления, где символы, из

которых состоит представление числа, не имеют самостоятельного

значения и имеют смысл только взятые в совокупности (например

коды Грея, Джонсона и др.).

И хотя в ВТ иногда используются непозиционные коды, и даже были разработаны ЭВМ, использующие эти коды, подавляющее число используемых в настоящее время компьютеров используют для представления чисел позиционные системы счисления.

Любое число в позиционной системе счисления может быть представлено в виде:

a_n·qⁿ + a_n-1·q^n-1 + … + a₁·q¹ + a₀·q⁰ + a_-1·q^-1 + a_-2·q^-2 +…+ a_-m·q^-m

где: a_i – цифра числа;

i – позиция цифры (отрицательные позиции определяют позиции

дробной части числа).

q – основание позиционной системы счисления.

В вычислительной технике используются следующие системы счисления.

1. Двоичная:

q = 2; {a_i} → 0,1;

Представление числа в двоичной системе счисления обычно обозначается символом B (Binary), поставленным в конце кода числа, например, 101011B.

1. Восьмеричная:

q = 8; {a_i} → 0,1,2,3,4,5,6,7;

Представление числа в восьмеричной системе счисления обозначается символом O (Octonory) или Q, например, 1735Q.

2. Десятичная:

q = 10; {a_i} → 0,1,2,3,4,5,6,7,8,9;

Представление числа в десятичной системе счисления либо подразумевается по умолчанию, либо обозначается символом D (Decimal), например, 12349D.

3. Шестнадцатеричная:

q = 16; {a_i} → 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F;

Представление числа в шестнадцатеричной системе счисления обозначается символом H (Hexadecimal), например, 1A9HCH.

4. Двоично-десятичная:

q = 10; {a_i} → 0,1,2,3,4,5,6,7,8,9;

но a_i – кодируется четырьмя двоичными разрядами.

Поскольку четырьмя двоичными разрядами можно закодировать до 16 символов, а кодируется только 10, то разновидностей двоично-десятичных кодов может быть много, в зависимости от весовых значений позиций этого четырехразрядного двоичного числа. В вычислительной технике наиболее широко используется двоично-десятичный код с весовыми значениями разрядов, соответствующими числам 8421. Поэтому для этого двоично-десятичного кода:

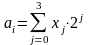где x_i = {0,1}; и ;

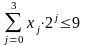Представление числа в двоично-десятичной системе счисления обозначается символами BCD (Binary Code Decimal).

Заметим, что при ручной записи на бумаге, систему счисления, в которой представлено число, бывает удобнее указывать в виде индекса после младшего разряда числа, например:

1011101₂ ; 101245₈ ; 23456₁₀ ; 7F5AC₁₆ ; 100101111000_2/10,

где индекс 2/10 указывает на двоично-десятичную систему счисления, в которой представлено число.

Правила перевода чисел из одной системы счисления в другую.

a) Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и наоборот.

Поскольку основания восьмеричной и шестнадцатеричной систем счисления кратны степени двойки (8 = 2³ , а 16 = 2⁴), то правила перевода двоичных чисел в восьмеричные и шестнадцатеричные, а также правила перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную, аналогичны и весьма просты.

Чтобы перейти от числа, представленного в двоичной системе счисления, к числам, представленным в восьмеричной или шестнадцатеричной системах счисления, необходимо исходное двоичное число разбить на группы, соответственно, по тройкам или четверкам и двоичные числа в каждой группе представить в виде восьмеричной или шестнадцатеричной цифры. Разбивка двоичного числа на группы двоичных разрядов должна происходить от дробной запятой вправо и влево.

Пусть будет дано двоичное число:

10111001100011010101,11001101101B

После разбивки на группы двоичных разрядов и кодирования каждой группы будем иметь:

2 7 1 4 3 2 5 6 3 3 2

010 111 001 100 011 010 101,110 011 011 010

B 9 8 D 5 C D A

1011 1001 1000 1101 0101,1100 1101 1010

Следовательно, данное двоичное число в восьмеричной и шестнадцатеричной системах счислений будет, соответственно, иметь вид:

2714325,6332Q и B98D5,CDAH;

Чтобы перевести число из восьмеричной или шестнадцатеричной систем счисления в двоичную систему, надо представить (развернуть) каждый символ исходного восьмеричного или шестнадцатеричного кода в виде двоичных чисел. Например:

111 101 011 010 , 100 101 001 B 1110 1101 1000 0011 0001 , 0010 0101 1001 B

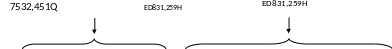
б) Перевод чисел из двоичной системы счисления в двоично-десятичную

и наоборот.

Не вызывает затруднений и перевод чисел из десятичной системы счисления в двоично-десятичную и наоборот, поскольку в двоично-десятичной системе каждая десятичная цифра представляется отдельно четырьмя двоичными разрядами (тетрадой) двоичных чисел. Например, при использовании двоично-десятичной системы с весами разрядов 8421 имеем:

в) Перевод чисел, представленных в двоичной, восьмеричной и

шестнадцатеричной системах счисления в десятичные числа.

Перевод чисел из указанных систем счисления в десятичную производится представлением данных чисел по общей формуле для позиционных систем счисления приведенной ранее. При этом все необходимые вычисления производятся в десятичной системе счисления. Приведем примеры.

1. Из двоичной системы счисления:

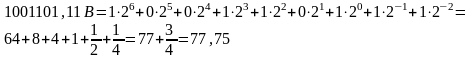
2. Из восьмеричной системы счисления:

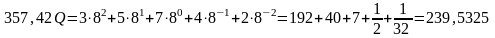
3. Из шестнадцатеричной системы счисления:

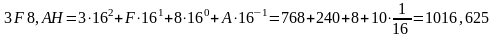
г) Перевод представления чисел из десятичной системы счисления в

двоичную, восьмеричную и шестнадцатеричную.

При изложении правил перевода представления чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную рассмотрим только те алгоритмы, в которых все требуемые арифметические вычисления осуществляются в десятичной системе счисления. В этом случае целая часть десятичного числа и дробная его часть преобразовываются по различным алгоритмам.

При преобразовании целого числа или целой части вещественного числа в другую позиционную систему счисления, алгоритм преобразования заключается в последовательном делении этого числа на основание требуемой системы счисления. Остатки от этого последовательного деления образуют последовательность цифр в искомой системе счисления. При этом, последний остаток будет являться первой цифрой искомого числа в требуемой системе счисления, а первый – последней.

Преобразование дробной части десятичного числа в дробную часть двоичного, восьмеричного или шестнадцатеричного числа осуществляется путем последовательного умножения этой дробной части на основание искомой системы счисления и выявлении получающейся целой части, при каждом умножении. Эти появляющиеся целые части будут являться цифрами целой части искомого числа в требуемой системе счисления. При этом цифры разрядов будут получаться в прямом порядке (цифрой старшего разряда дробной части числа является первая, полученная после умножения целая часть). Окончание преобразования дробной части числа определяется появлением всех нулей в разрядах, отводимых под дробную часть. Если же такое последовательное умножение до получения нулей в дробной части произведения продолжается очень долго, то, в таких случаях преобразование дробной части числа осуществляется до требующейся погрешности (числа знаков в дробной части).

Для уяснения алгоритмов преобразования десятичных чисел в двоичные, восьмеричные и шестнадцатеричные ниже приведены примеры таких преобразований.

а) Преобразование десятичного числа 419,8125 в двоичную форму

представления.

Преобразование целой части			Преобразование дробной части
Целая часть числа или частного	Делитель	Остаток	Дробная часть числа или произведения	Множитель	Целая часть после умножения
419	2	1	0,8125	2	1
209	2	1	0,6250	2	1
104	2	0	0,2500	2	0
52	2	0	0,5000	2	1
26	2	0	0,0000
13	2	1
6	2	0
3	2	1
1	2	1
0

Результат: 110100011,1101В.

б) Преобразование десятичного числа 551,9375 в восьмеричную форму

представления.

Преобразование целой части			Преобразование дробной части
Целая часть числа или частного	Делитель	Остаток	Дробная часть числа или произведения	Множитель	Целая часть после умножения
551	8	7	0,9375	8	7
68	8	4	0,5000	8	4
8	8	0	0,0000
1	8	1
0

Результат: 1047,74Q.

в) Преобразование десятичного числа 895,253 в шестнадцатеричную форму представления.

Преобразование целой части			Преобразование дробной части
Целая часть числа или частного	Делитель	Остаток	Дробная часть числа или произведения	Множитель	Целая часть после умножения
895	16	15	0,253	16	4
55	16	7	0,048	16	0
3	16	3	0,768	16	12
0			0,288	16	4
			0,608	16	9
			0,728	16	11
			0,648	16	10
			…	…	…
			…	…	…

Результат: 37,40C49BAH

Прямой, обратный и дополнительный коды чисел.

Прямым кодом называется код (последовательность цифр), который получается при формировании числа в заданной системе счисления.

Обратным кодом называется код, дополняющий прямой код до кода максимально возможного значения числа в данной системе счисления с тем же количеством разрядов.

Дополнительным кодом называется код, дополняющий прямой код до кода числа, равного весу единицы следующего за старшим разряда.

Приведем примеры обратных кодов чисел в разных системах счисления.

Десятичная:

999 - 531 = 468 → обратный код десятичного числа 531.

Шестнадцатеричная:

FFF – D54 =2AB → обратный код шестнадцатеричного числа D54.

Двоичная:

11111111 – 10011101 = 01100010 → обратный код двоичного числа 10011101.

Отметим, что обратный код двоичного числа можно получить просто заменив все единицы прямого кода на нули, а нули на единицы.

Примеры дополнительных кодов чисел в разных системах счисления.

Десятичная:

1000 – 531 = 469 → дополнительный код десятичного числа 531.

Шестнадцатеричная:

1000 – D54 = 2AС → дополнительный код шестнадцатеричного числа D54.

Двоичная:

100000000 – 10011101 = 01100011 → дополнительный код двоичного числа

10011101.

Следовательно, дополнительный код числа в любой системе счисления можно получить, прибавив к его обратному коду единицу в младший разряд.

В вычислительной технике обратные и дополнительные коды используются при представлении отрицательных чисел, что существенно облегчает осуществление арифметических операций со знаковыми числами. Процесс преобразования прямых кодов в обратные в самих компьютерах, при двоичной системе счисления, весьма прост. Обратный код просто снимается с инверсных выходов триггеров регистров, хранящего прямой код числа.

Преобразование прямых кодов чисел в дополнительные несколько более сложен, так как при прибавлении 1 к значению младшего разряда числа могут возникнуть переносы, в худшем случае, во всех разрядах данного числа. А это может существенно увеличить время преобразования и требует регистров, оборудованных цепями переноса. Однако, с другой стороны, использование обратных кодов, при осуществлении арифметических операций требует сумматоров с циклическим переносом, т.е. с цепью переноса единицы переполнения (переноса из самого старшего разряда) в младший разряд и суммирования с ним.

В современных компьютерах для представления отрицательных чисел используются, как правило, дополнительные коды.

Кодирование в компьютерах целых чисел.

Целые числа могут быть числами без знака (например: адреса команд и данных, число циклов, число сдвигов, число элементов строк, число строк и столбцов матриц и т.п.) и со знаком.

а) Числа без знака представляются в компьютерах прямым кодом.

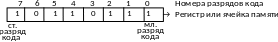б) Числа со знаком представляются кодом, в котором первый разряд

кода числа является символом знака: 0 – положительного числа,

1 – отрицательного числа.

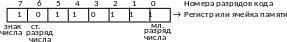
При этом все отрицательные числа представляются в дополнительном коде.

Поэтому в первом примере, представленное число будет иметь значение равное (в десятичной форме представления): 183, а во втором: -73.

Кодирование в компьютерах вещественных чисел.

Все вещественные числа в компьютерах представляются в полулогарифмическом формате, или, так называемом формате чисел с плавающей запятой (точкой), и всегда со знаком.

N = S^p·q

где: S – основание системы счисления;

p – порядок основания, или, как обычно говорят, просто порядок;

q – мантисса.

В современных компьютерах основание системы счисления всегда равно 2 и поэтому для них N = 2^p·q.

Мантисса числа в мэйнфреймах, типа IBM 360/370 и ЕС ЭВМ, должны удовлетворять требованию: 1 > q ≥ 0,5, т.е. должна быть в пределах: 0,111…1 ≥ 0,100…0.

Мантисса числа q для наиболее распространенных современных персональных компьютеров корпорации Intel принята несколько другой. Она должна удовлетворять требованию: 2 > q ≥ 1,5, то есть должна быть в пределах 1,111…1≥q≥1,000…0.

Таким образом, в полулогарифмическом виде представление числа -110,0101 в персональных компьютерах будет: -2⁺²·1,100101, а числа +0,011101 будет: +2^-2·1,1101.

Представленное в таком виде число называется нормализированным и в этом виде хранится в памяти. Если в результате проведения арифметической операции представление результата выходит за рамки нормализированного представления, результат автоматически нормализируется при передаче в память.

Формат вещественных чисел, размещенных в ячейках памяти, на примере конкретного формата короткого вещественного, приведен на рис.V.1.1.

Рис. 5.1.1. Размещение в ячейках памяти элементов представления

вещественных чисел в формате КВ (короткое вещественное).

Заметим, что поскольку первый разряд значения мантиссы всегда должен быть равен 1, то он фактически в оперативной памяти не фиксируется, но всегда подразумевается. На этом экономится объем памяти, необходимой для хранения данных.

Поскольку порядок числа есть целое число со знаком, то старший разряд порядка должен содержать знак порядка. В начальный период развития компьютерной техники так и было. Однако операции с порядками, которые имеют место почти всегда при обработке вещественных чисел, затрудняются тем, что порядок представляется числом со знаком. Поэтому в современных компьютерах используются исключительно так называемые смещенные порядки. Для получения смещенного порядка к исходному значению порядка прибавляется некоторое смещение А. Это смещение А, представляет собой положительное число, равное максимальному абсолютному значению исходного порядка, как числа со знаком. В результате полученное значение смещенного порядка будет всегда иметь положительное значение и операции с порядками существенно упрощаются. В качестве смещения А, для восьмиразрядного значения порядка (при формате КВ), можно брать либо число 10000000 либо число 01111111. При этом , все положительные порядки, в смещенном виде будут иметь в старшем разряде 1, а все отрицательные – 0.

В случае смещения А = 10000000, при нулевом значении исходного порядка, смещенный порядок будет равен: А + 0 = 10000000. Поэтому говорят, что имеет место смещенный порядок с положительным нулем.

В случае смещения А = 01111111, при нулевом значении исходного порядка, смещенный порядок будет равен: А + 0 = 01111111. Поэтому говорят, что в этом случае имеет место смещенный порядок с отрицательным нулем.

Отметим, что в большинстве персональных компьютеров обычно используется смещенный порядок с отрицательным нулем. И, например, число: -110,0101В, в полулогарифмическом виде (в форме представления с плавающей запятой) имеющее вид: -2⁺²·1,100101, в формате короткого вещественного (КВ) со смещенным порядком с отрицательным нулем, в ячейке памяти разместиться так, как показано на рис. V.1.2.

Рис. 5.1.2. Размещение в ячейке памяти числа: -110,0101 в формате КВ со

смещенным порядком с отрицательным нулем.

Отметим, при этом, очень важное обстоятельство: мантиссы как положительных, так и отрицательных чисел в памяти, в отличие от целых чисел, всегда представляются в прямых кодах! И, поскольку, при операциях с мантиссами их рассматривают как целые числа со знаком, то при осуществлении арифметических операций над ними, мантиссы отрицательных чисел, вызываемые из памяти в узел обработки (арифметико-логическое устройство), обязательно должны преобразовываться и представляться в дополнительном коде.