1.10. Некоторые формулы структурной кристаллографии

1.Угол между плоскостями. При решении некоторых задач структурного анализа положение плоскости часто характеризуют направлением нормали к ней. Это используется для широко распространенных ортогональных кристаллов, так как в этом случае индексы плоскости (h,k,l) и нормали к ней [h,k,l] совпадают. Для них при определении угла между плоскостями достаточно вычислить угол между их нормалями. Докажем это. Пусть плоскость с индексами (h,k,l) отсекает на осях отрезки OA, OB, OC и является ближайшей к началу координат из данного семейства плоскостей.

Поскольку отрезки, отсекаемые плоскостью на осях, обратно пропорциональны индексам плоскости, то можно записать:

OA=a/h, OB=b/k, OC=c/l

Допустим, что прямая ON имеет те же индексы [hkl], и в векторной форме мы можем записать эту прямую как

ON = h a + k b+ l c

Если прямая [h k l], действительно, перпендикулярна (h k l), то вектор ON должен быть перпендикулярен любой прямой, лежащей в этой плоскости, например AB, и их скалярное произведение должно быть равно нулю:

(ON  AB)  0.

Рассмотрим его величину

(ON  AB) = {ON ( b/k - a/h)} = {( ha+ kb+lc) (b/k-a/h)}= h/k(ab) + b² + l/k(c b) - a² -k/h(ba) - l/h(ca)  0

Чтобы левая часть обратилась в нуль, необходимо и достаточно:

1) (a  b) = (c  b) = (b  a) = (c  a) = 0, что справедливо для случая сингоний, где  =  =  = 90

2) a = b.

Взяв затем вместо AB другие прямые в плоскости (hkl): BC, AC и проведя аналогичные рассуждения, получим дополнительные требования a=c и b=c.

Таким образом, тождество выполняется для кубической сингонии, и можно считать доказанным, что плоскость и нормаль к ней в кубической решетке всегда имеют одинаковые индексы.

В этой сингонии угол между плоскостями (равный углу между нормалями к плоскостям) можно записать на основании соотношения (1.4) как

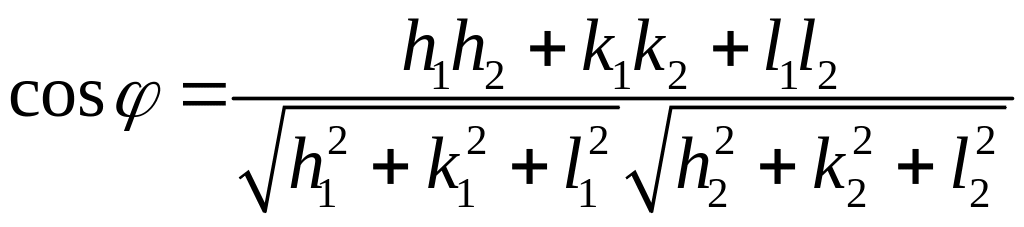(1.11)

Выразим при помощи кристаллографических индексов и основные величины в элементарной ячейке: период идентичности, межплоскостное расстояние и объем элементарной ячейки.

2. Период идентичности. Под периодом идентичности подразумевают расстояние между ближайшими идентичными узлами, лежащими на одной прямой. Он обозначается через I.

Периоды идентичности по осям координат равны длинам трансляций a, b, c. Период идентичности вдоль произвольного направления равен вектору:

I = ma + nb+ pc , (1.12)

где m, n, p - координаты узла, лежащего на этом направлении и ближайшего к началу координат. (Числа m, n, p могут не совпадать с индексами прямой, параллельной этому направлению, но всегда им кратны).

Абсолютное значение вектора I можно найти из квадратичного выражения:

(1.13)

что для кубической системы I составляет:

(1.14)

3. Объем элементарной ячейки. Объем параллелепипеда, как известно, равен произведению площади основания на высоту. Если элементарная ячейка построена на векторах a, b, c, то площадь основания S будет равна

или (1.15)

Тогда объем элементарной ячейки элементарной ячейки V равен:

Окончательно

Аналогично имеем:

(1.16)

Раскрытие этих скалярных произведений дает:

(1.17)

Естественно, что для ортогональных сингоний выражение (1.17) упрощается:

(1.18)

или для кубической сингонии:

(1.19)

4. Межплоскостное расстояние. Межплоскостное расстояние d – это расстояние между соседними параллельными плоскостями кристалла. Оно равно длине перпендикуляра, опущенного из начала координат на плоскость, ближайшую к началу координат. Величина d связана с индексами соответствующих плоскостей.

Возьмем для простоты решетку с ортогональной системой координат. Плоскость (hkl) отсекает на осях x, y, z отрезки OA, OB, OC, равные а/h, b/k, c/l соответственно. Если ON перпендикуляр, опущенный из начала координат к этой плоскости, то по условию |ON|= d и из треугольника OAN получим ON/OA= cos  или dh/a=cos.

Аналогично: dk/b= cos; dl/c= cos.

Как известно, для ортогональной системы координат выполняется равенство:

(1.20)

Отсюда 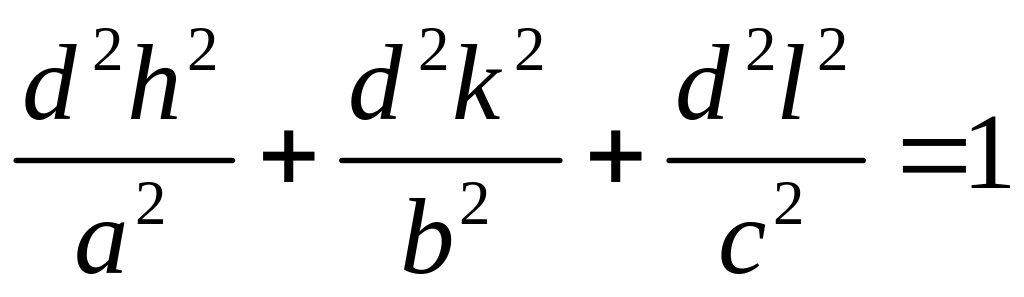или 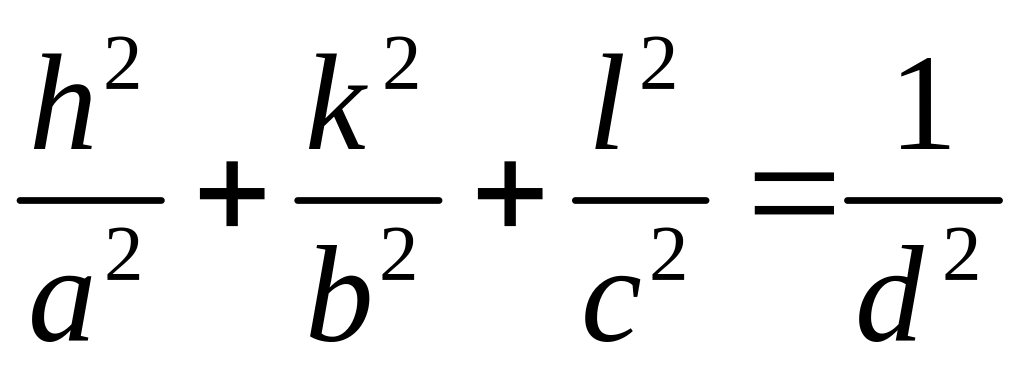(1.21)

Соотношение (1.21) – квадратичная формула для ортогональных сингоний. Она справедлива, например, для ромбической сингонии, где a  b  c, но  =  =  = 90. Исходя из формулы 1.21, будем иметь:

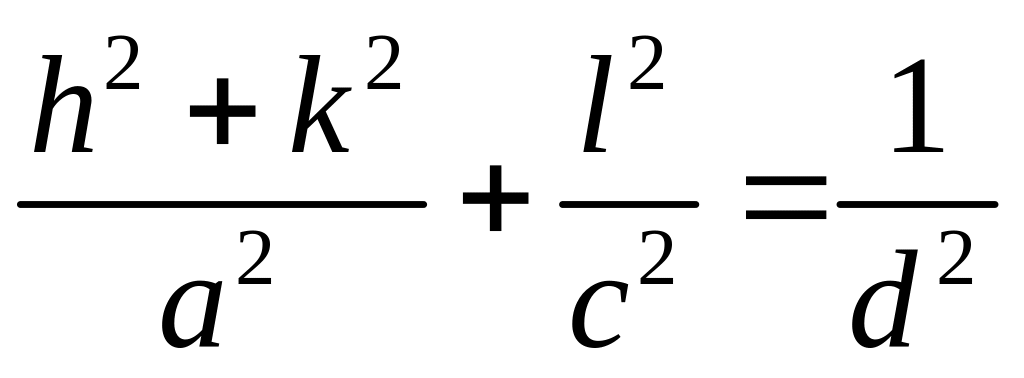(1.22)

Для кубической сингонии a = b = c и  =  =  = 90:

(1.23)

Таким образом, межплоскостное расстояние связано с кристаллографическими индексами плоскости и параметрами элементарной ячейки.