8.Евклидовы пространства. Норма вектора. Ортонормированный базис. Процесс ортогонализации. Неравенство Коши-Буняковского.

Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность равную 3.

В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов, определённых ниже. Обычно  -мерное евклидово пространство обозначается  , хотя часто используется не вполне приемлемое обозначение  .

1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство   с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:

,

в простейшем случае (евклидова норма):

где   (в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).

2. Метрическое пространство, соответствующее пространству описанному выше. То есть с метрикой, введённой по формуле:

,

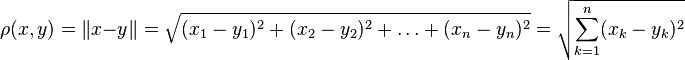где   и  .

3. Вообще любое предгильбертово пространство (пространство со скалярным произведением  ). Норма вектора[править | править исходный текст]

Норма в векторном пространстве   над полем вещественных или комплексных чисел — это функционал  , обладающий следующими свойствами:

1. 

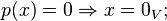
2. (Неравенство треугольника);

3. 

Эти условия являются аксиомами нормы.

Векторное пространство с нормой называется нормированным пространством, а условия (1-3) — также аксиомами нормированного пространства.

Нетрудно видеть, что из аксиом нормы вытекает свойство неотрицательности нормы:

Действительно:

Из 3 получаем, что  . Теперь из 2 получаем  . Таким образом,  .

Чаще всего норму обозначают в виде:  . В частности,   — это норма элемента   векторного пространства  .

Вектор с единичной нормой ( ) называется нормальным или нормированным.

Любой ненулевой вектор   можно нормировать, то есть разделить его на свою норму: вектор   имеет единичную норму. С геометрической точки зрения это значит, что мы берем сонаправленный вектор единичной длины.

Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами.

Последнее удобно записывается при помощи символа Кронекера:

9.Линейные операторы. Их свойства и действия над ними. Обратный оператор. Преобразование матрицы линейного оператора. Подобные матрицы. Линейным преобразованием (линейным оператором) линейного пространства   называется линейное отображение   пространства   в себя.

Поскольку линейное преобразование является частным случаем линейного отображения, к нему применимы все понятия и свойства, рассмотренные для отображений: инъективность, сюръективность, биективность, обратимость, ядро, образ, дефект, ранг и т.д.

Матрицей линейного оператора (преобразования)   в базисе   пространства  называется квадратная матрица  , составленная из координатных столбцов образов базисных векторов  , найденных относительно базиса  .

Матрица биективного линейного оператора (преобразования) обратима, т.е. невырождена. Поэтому биективное (обратимое) преобразование называют также невырожденным.

10.Линейные операторы в евклидовом пространстве. Сопряженные и самосопряженные операторы. Собственные векторы и собственные значения. Канонический вид матрицы.  Операторы в евклидовом пространстве и их продолжение на комплексификацию.

В евклидовом пространстве для оператора 9 определяется сопряженный оператора 10 той же формулой 11 при любых х и у, что и в унитарном пространстве. Доказательство существования и единственности сопряженного оператора ничем не отличается от аналогичных доказательств для унитарного пространства. Матрица оператора 12 в ортонормальном базисе просто транспонирована с матрицей оператора 13 При продолжении взаимно сопряженных операторов 14 с S на 15 они останутся сопряженными.

Действительно,