Декартовы прямоугольные координаты в пространстве. Координаты точек. Координаты векторов. Деление отрезка в данном отношении

Декартова прямоугольная система координат в пространстве определяется заданием единицы масштаба для измерения длин и трех пересекающихся в точке взаимно перпендикулярных осей, первая из которых называется осью абсцисс , вторая – осью ординат , третья – осью аппликат ; точка ‑ начало координат. Положение координатных осей можно задать с помощью единичных векторов , направленных соответственно по осям . Векторы называются основными или базисными ортами и определяют базис в трехмерном пространстве.

2.Различные формы произведения векторов. Условие ортогональности, коллинеарности и компланарности векторов. Скалярное произведение

Скалярными произведением двух векторов и называется число, равное произведению их длин на косинус угла между ними: .

Скалярное произведение обладает следующими свойствами:

1. ;

2. ;

3. ;

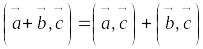4. Если и ‑ ненулевые векторы, то тогда и только тогда, когда эти векторы перпендикулярны. Если , то угол между и - острый, если , то угол - тупой;

5. Скалярный квадрат вектора равен квадрату его длины, т.е. .

Следовательно, .

Векторное произведение

Векторным произведением вектора на вектор называется вектор , длина и направление которого определяется условиями:

1. , где 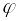‑ угол между и ;

2. перпендикулярен каждому из векторов и ;

3. направлен так, что кратчайший поворот от к виден из его конца совершающимся против часовой стрелки.

Векторное произведение обладает следующими свойствами:

1. ;

2. ;

3. ;

4. Векторное произведение равно нулю (нуль вектору) тогда и только тогда, когда и коллинеарны. В частности, для любого вектора ;

5. Если и неколлинеарны, то модуль векторного произведения равен площади параллелограмма 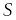построенного на этих векторах, как на сторонах.

Смешанное произведение

Смешанным произведением тройки векторов , и называется число, равное скалярному произведению вектора на векторное произведение . Если рассматриваемые векторы , и некомпланарны, то векторное произведение есть вектор, длина которого численно равна площади построенного на них параллелограмма. Направлен этот вектор по нормали к плоскости параллелограмма. Если этот вектор скалярно умножить на вектор , то получившееся число будет равно произведению площади основания параллелепипеда, построенного на тройке векторов , и , и его высоты, т.е. объему этого параллелепипеда.

Таким образом, смешанное произведение векторов (которое обозначается ) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах , и .

Знак произведение положителен, если векторы , и , образуют правую тройку векторов, т.е. вектор направлен так, что кратчайший поворот от к виден из его конца совершающимся против часовой стрелки.

Из геометрического смысла смешанного произведения непосредственно следует необходимое и достаточное условие некомпланарности векторов , и : для того, чтобы векторы , и были некомпланарными необходимо и достаточно, чтобы их смешанное произведение было отлично от нуля.

Определение.

 Вектора a и b называются ортогональными, если угол между ними равен 90°. 

Условие ортогональности векторов.

Два вектора a и b ортогональны (перпендикулярны), если их скалярное произведение равно нулю.

a · b = 0

Определение.

 Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами

Два вектора будут коллинеарны при выполнении любого из этих условий:

Условие коллинеарности векторов 1.

 Два вектора a и b коллинеарны, если существует число n такое, что

a = n · b

Условия коллинеарности векторов 2.

 Два вектора коллинеарны, если отношения их координат равны. N.B. Условие 2 неприменимо если один из компонентов вектора равен нулю.

Условия коллинеарности векторов 3.

 Два вектора коллинеарны, если их векторное произведение равно нулевому вектору. N.B. Условие 3 применимо только для трехмерных (пространственных) задач.

Определение.

 Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.

Всегда возможно найти плоскости параллельную двум произвольным векторам, по-этому любые два вектора всегда компланарные.

Условия компланарности векторов

Для 3-х векторов.

 Три вектора компланарны если их смешанное произведение равно нулю.

Для 3-х векторов.

 Три вектора компланарны если они линейно зависимы.

Для n векторов.

 Вектора компланарны если среди них не более двух линейно независимых векторов.