Локальный экстремум
Точка
называется точкой локального
максимума
функции
,
если существует интервал
,
содержащий точку
такой что
.
Точка
называется точкой локального
минимума
функции
,
если существует интервал
,
содержащий точку
такой что
.
Точки локального минимума и локального максимума называются точками локального экстремума.
Необходимым
условием локального экстремума
дифференцируемой функции является
выполнение равенства
.
Поэтому точки, в которых дифференцируемая
функция может иметь локальный экстремум,
находят, решая уравнение:
.
Решения этого уравнения называют стационарными точками.
Глобальный экстремум
Непрерывная
на отрезке
функция
принимает свое наибольшее значение
и свое наименьшее значение
в точках этого отрезка. Эти значения
могут достигаться либо в стационарных
точках отрезка, либо в точках
недифференцируемости функции, либо в
граничных точках отрезка. Поэтому для
нахождения значений
и
поступают следующим образом.
Находят стационарные точки
функции;Находят точки
,
в которых производная
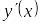не существует или обращается в
бесконечность;Вычисляют значения:
‑ и
выбирают среди этих чисел наибольшее
и наименьшее.
Это и будут и ‑ глобальные экстремальные значения.
24.Свойства комплексных чисел. Разложение многочленов на множители. Представление рациональной функции в виде суммы элементарных дробей.
Комплексные
числа —
числа вида 
,
где
и 
—
вещественные числа, 
— мнимая
единица;
то есть 
.
Множество всех комплексных чисел обычно
обозначается 
Первоначально идея о необходимости расширения понятия действительного числа возникла в результате формального решения квадратных и кубических уравнений, в которых в формулах для корней уравнения под знаком корня стояло отрицательное число. В дальнейшем возникшая теория функций комплексного переменного нашла применение для решения многих задач во всех областях математики и физики.
Тождественное преобразование, приводящее к произведению нескольких множителей - многочленов или одночленов, называют разложением многочлена на множители. В этом случае говорят, что многочлен делится на каждый из этих множителей.
-Вынесение общего множителя за скобки. Это преобразование является непосредственным следствием распределительного закона ac + bc = c(a + b).
-Использование формул сокращенного умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения.
-Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведени.
-Способ выделения полного квадрата. Метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов.
Для
интегрирования рациональной функции 
,
где P(x) и Q(x) -
полиномы, используется следующая
последовательность шагов:
Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;
Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;
Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
Вычислить интегралы от простейших дробей.
25.Первообразная. Неопределенный интеграл и его свойства. Таблица интегралов. Основные методы вычисления.
Понятие неопределенного интеграла
Интегрирование
–
операция,
обратная дифференцированию, которая
позволяет определять функцию
,
для которой заданная функция
является ее производной:
.
Другими словами, если операция дифференцирования состоит в нахождении производной, то интегрирование – это операция отыскания первообразной.
Функция
называется первообразной для функции
,
на промежутке
,
если для каждой точки этого промежутка
.
Теорема.
Если
и
– любые две первообразные для данной
функции
на промежутке
,
то для всех
выполняется равенство
.
Доказательство:
Таким
образом, все семейство первообразных
для данной функции
имеет вид
,
где
одна из первообразных, а
произвольная постоянная.
Совокупность всех первообразных для функции на промежутке называется неопределенным интегралом функции .
Неопределенный интеграл обозначается следующим образом:
,
где
знак интеграла;
подынтегральная
функция;
подынтегральное
выражение.
Свойства неопределенного интеграла
1.Производная неопределенного интеграла равна подынтегральной функцией:
2.
Эти свойства означают, что интегрирование и дифференцирование – взаимно обратные операции.
3.Если
и
– интегрируемые функции, т.е. на
промежутке
они имеют первообразные, то сумма
функций
также интегрируема и
.
4.Если
– интегрируемая функция, а
постоянная величина, то
– также интегрируемая функция и
.
Таким образом, свойства 3 и 4 указывают на линейность операции интегрирования:
,
где
постоянные;
интегрируемые
функции.
5.Если
,
а также
дифференцируемая функция, то
.
Простым обращением известных формул дифференцирования элементарных функций получается таблица простейших неопределенных интегралов.
;
;
;
;
;
;
;
;
;
;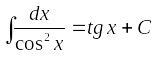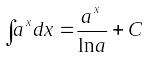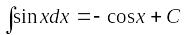