Точки разрыва

Непрерывность функции в точке , т.е. выполнение условия (3), означает, что оба односторонних предела и существуют и равны , т.е.

.

Если условие (4) не выполнено, то точку называют точкой разрыва функции . Условие (4) означает выполнение следующих четырех условий, каждое из которых предполагает выполнение всех предыдущих:

1. и существуют;

2. и конечны;

3. ;

4. .

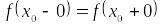Если 1. не выполнено, то называют точкой неопределенности.

Если 1. выполнено, а 2. не выполнено, то называют точкой бесконечного скачка.

Если выполнены 1. и 2., а 3. не выполнено, то называют точкой конечного скачка. Величина называется скачком функции в точке .

Если 1., 2., 3. выполнены, а 4. не выполнено, то называют точкой устранимого разрыва.

Если функция определена в окрестности точки и не определена в самой точке , то также называют точкой разрыва. Такие точки классифицируют по той же схеме.

Сравнение бесконечно малых величин:

• Две бесконечно малые величины и называются бесконечно малыми одного порядка, если предел их отношения есть конечное число, отличное от нуля, т.е. ;

• Величина называется бесконечно малой величиной высшего порядка по сравнению с , если предел отношения к равен нулю, т.е. ;

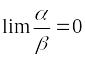• Величина называется бесконечно малой величиной низшего порядка по сравнению с , если предел отношения к является бесконечно большой величиной, т.е. ;

• Две бесконечно малые величины и называются эквивалентными бесконечно малыми, если предел их отношения равен единице, т.е. .

18.Функции, непрерывные на отрезке, и их свойства. Равномерная непрерывность. Равномерная непрерывность

        важное понятие математического анализа. Функция f (x) называется равномерно-непрерывной на данном множестве, если для всякого ε > 0 можно найти такое δ = δ(ε) > 0, что |f (x₁) — f (x₂)|<ε для любой пары чисел x₁ и x₂ из данного множества, удовлетворяющей условию |x₁—x₂|< δ (ср. Непрерывная функция). Например, функция f (x) = x² равномерно непрерывна на отрезке [0, 1]: если  x₁ ≤ 1, 0 ≤ x₂ ≤ 1 обязательно |x₁ + x₂|≤ 2). Вообще функция, непрерывная в каждой точке отрезка [а, b], равномерно непрерывна на этом отрезке (теорема Кантора). Для интервала эта теорема может не иметь места.

         Так, например, функция   непрерывна в каждой точке интервала 0 < x < 1, но не является равномерно непрерывной в этом интервале, потому что, например, при ε = 1 для любого δ > 0 (δ < 1) мы имеем удовлетворяющие неравенству |x₁ — x₂| < δ числа x₁ =   и x₂= δ , для которых 

19.Понятие производной, ее геометрический и физический смысл. Основные правила дифференцирования. Таблица производных.

Определение и смысл производной

Понятие производной является одним из основных понятий дифференциального исчисления, производная используется при исследовании процессов, в том числе и экономических, описываемых функциями. При исследовании приращения зависимой величины , обусловленного приращением независимой переменной , часто возникает необходимость определения предела отношения этих величин . Этот предел называется производной, а операция его вычисления – дифференцированием функции.