Бесконечный предел

Наряду с бесконечно малыми существуют и бесконечно большие величины, являющиеся обратными по отношению к бесконечно малым. Поэтому является бесконечно большой ( , при ), если такое, что при .

Говорят, что предел последовательности равен , если для такое, что выполняется неравенство: .

В отличие от бесконечно малых последовательностей, бесконечно большие могут не иметь предела. Например, по модулю неограниченно растет, но сама величина не имеет определенного стремления.

Свойства пределов:

Пределы обладают следующими свойствами:

• Если 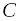– есть постоянная функция, то ;

• Если существуют 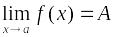, и в некоторой окрестности точки функция ограничена, т.е. , тогда ;

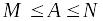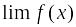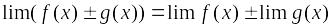• Если существуют и при каком-то условии, то (при том же условии). Это свойство справедливо для любого конечного числа функций;

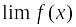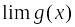• Если существуют и при каком-то условии, то (при том же условии). Это свойство также справедливо для любого конечного числа функций, в частности, справедлива формула ;

• Если существуют и 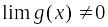при каком-то условии, то (при том же условии);

• Если и существуют , и , то .

Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей.

Число «e» — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера иличислом Непера. Обозначается строчной латинской буквой «e».Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.

17.Предел функции. Понятие непрерывности и свойства функций, непрерывных в точке. Точки разрыва. Замечательные пределы. Сравнение бесконечно малых. Непрерывность функции

Рассмотрим функцию , определенную на промежутке Пусть . Функция называется непрерывной в точке , если

Функция называется непрерывной слева (справа) в точке , если . Естественно, при этом функция должна быть определена в некоторой окрестности слева (справа) то точки . Непрерывность функции в точке означает непрерывность этой функции в указанной точке как слева, так и справа.

Функция , определенная на интервале называется непрерывной на интервале , если она непрерывна в каждой точке этого интервала .

Функция , определенная на отрезке ( ) называется непрерывной на отрезке , если она непрерывна в каждой точке интервала , непрерывна справа в точке и непрерывна слева в точке .

Общие свойства непрерывных функций, заданных на отрезке , определяются четырьмя теоремами: двумя теоремами Больцано–Коши и двумя теоремами Вейерштрасса.

Теорема (первая теорема Больцано–Коши). Пусть функция определена и непрерывна на отрезке , и на концах этого промежутка принимает значения разных знаков; тогда найдется точка , в которой функция равна нулю.

Теорема (вторая теорема Больцано–Коши). Пусть функция определена и непрерывна на отрезке . Тогда, если то функция принимает все свои промежуточные значения, принадлежащие промежутку , где , , т.е. .

Теорема (первая теорема Вейерштрасса). Пусть функция определена и непрерывна на отрезке , тогда функция является ограниченной на этом отрезке.

Теорема (вторая теорема Вейерштрасса). Пусть функция определена и непрерывна на отрезке , тогда функция имеет минимум и максимум на этом отрезке (множество значений функции включает в себя точные верхнюю и нижнюю границы).