Решение транспортных задач в виде сетевой модели без ограничения пропускной способности сети

Постановка задачи

Классическая транспортная задача предусматривает перевозку грузов из пунктов-поставщиков в пункты-потребители. При этом каждый отправитель связан с пунктом-потребителем отдельной дорогой с характерными именно для нее затратами на перевозку. Однако на практике, как правило, некоторые пути, связывающие два пункта, проходят через другие пункты. Более того, окажется возможным провести груз из одного пункта в другой несколькими путями. Поэтому подобные задачи формируют не в матричной, а в сетевой постановке.

На сети с вершинами (n) и дугами (m) находится множество по­ставщиков (А) и потребителей (В). Известны ресурсы i-x поставщиков (а_i) и потребности j-x потребителей (b_j.). Задана стоимость (длина пути) перевозки грузов (С_ij) по каждой дуге. При этом требуется обеспечить минимум стоимости перевозки (минимум совокупной транспортной работы), т.е. необходимо минимизировать целевую функцию Z=ΣC_ij∙X_ij→min при следующих необходимых условиях Σa_i=Σb_j и неотрицательных величинах грузопотоков (X_ij).

Общий алгоритм

Общий алгоритм решения подобных задач рассмотрим на ст дующем примере. На рис. 8.11 изображена транспортная сеть. При этом числовые значения в скобках со знаком «-» означают потребности соответствующих пунктов, со знаком «+» – наличие товав на складе.

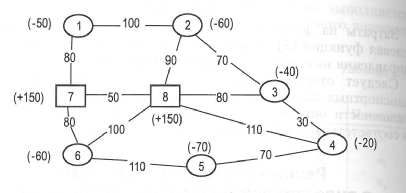
Рис. 8.11. Транспортная сеть

Шаг 1. Проверяем главное условие равенства ресурсов поставщиков и спроса потребителей. Условие выполняется. Следовательно, можем приступать к решению задачи.

Шаг 2. Составляем исходный план (рис. 8.12), при котором ресурсы поставщиков должны быть отправлены, а спрос потребителей удовлетворен (на рис. 8.12 стрелками показаны направления грузопотоков, числа обозначают количество перевозимой продукции).

Шаг 3. Присваиваем потенциалы вершинам так, чтобы впоследствии не иметь дело с отрицательными числами. Например, вершине 7 – потенциал, равный 300. Назначаем потенциалы остальным вершинам, придерживаясь следующего правила: при движении по дугам сети в направлении следования грузопотока к потенциалу предыдущей вершины прибавляем длину дуги, а при движении по дугам против потока эту длину из потенциала предыдущей вершины вычитаем (рис. 8.12).

Если невозможно назначить потенциалы всем вершинам относи­тельно одной заданной (в нашем случае – вершина 7), транспортная сеть разбивается на отдельные (независимые) части, оптимизация которых возможна или с применением метода оптимизации коль­цевых маршрутов, или в виде сетевой модели.

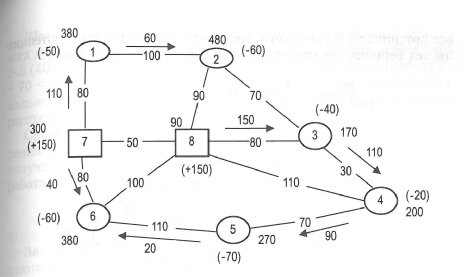
Рис. 8.12. Исходный план распределения ресурсов

Шаг 4. Проверяем выполнение условия оптимальности для всех дуг сети, на которых нет грузопотока, т.е. соблюдение выражения

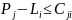
где Р_j – потенциал в j-м пункте (стоимость у потребителя); L_i – потенциал в i-м пункте (стоимость у поставщика); С_ji – расстояние между пунктами (стоимость транспортировки).

Такими дугами (парами пунктов) являются: 2-3 (480-170=310>70); 7-8 (300-90=210>50); 4-8 (200-90=110=110); 6-8 (380-90=290>100); 2-8 (480-90=390>90). Условие оптимальности нарушено на четырех дугах из пяти, следовательно, исходный план неоптимальный.

Шаг 5. Выбираем дугу 2-8 с максимальным нарушением усло­вия оптимальности и направляем по ней грузопоток от вершины с меньшим потенциалом (8) до вершины с большим потенциалом (2). Далее необходимо составить замкнутый контур, состоящий из дуг с потоком и выбранной дуги с нарушением. Это можно сделать един­ственным способом, составив контур из дуг 8-2, 2-1, 1-7, 7-6, 6-5, 5-4, 4-3, 3-8. Продвигаясь по этому контуру от точки 8 к точке 2 и далее - к точке 8, находим наименьший встречный поток (20). Прибавляя это число ко всем попутным грузопотокам и вычитая его из всех встречных, получаем улучшенный вариант перевозок (рис. 8.13). Повторяем шаг 3. Нет необходимости заново подсчитывать все потенциалы вершин сети, достаточно исправить лишь потенциа­лы тех вершин, где изменилось направление грузопотоков.

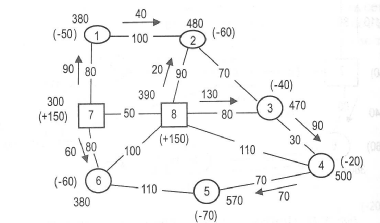
Рис. 8.13. Первый улучшенный вариант распределения ресурсов

Шаг 6. Проверяем снова выполнение условия оптимальности для всех дуг сети, на которых нет грузопотока: 2-3 (480-470=10<70), 8-7 (390-300=90>50), 8-6 (390-380=10<100), 5-6 (570-380=190>110), 4-8 (500-390=110=110). Условие не выполняется на двух дугах из пяти. При этом наибольшее нарушение отмечено на дуге 5-6. Повторяя шаг 5, получаем второй улучшенный план распределения ресурсов (рис. 8.14).

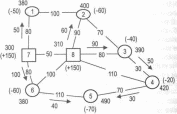
Рис. 8.14. Второй улучшенный вариант распределения ресурсов

Шаг 7. Вновь проверяем выполнение условия оптимальности для всех дуг сети, на которых нет грузопотока: 2-1 (400-380=20<100), 2-3 (400-390=10<70), 4-8 (420-310=110=110), 6-8 (380-310=70<100), 8-7 (310-300=10<50). На всех дугах условие оптимальности выполняется, следовательно, второй улучшенный план распределения ресурсов оптимален.

Сравнивая исходный и второй улучшенный планы распределения ресурсов по показателю совокупной транспортной работы, получаем, что в результате оптимизации совокупная транспортная работа (транспортные расходы) уменьшилась (снизились) на 22%.