2. Задание орграфа с помощью матриц

Понятие о смежности и инцидентности распространяется на ориентированные графы.

Две вершины называются смежными, если существует дуга соединяющая их.

Две дуги называются смежными, если они имеют общую вершину.

Дуга (x_i, x_j) называется инцидентной каждой из вершин x_i и x_j.

Вершина x_i называется инцидентной дуге, входящей в эту вершину или исходящей из этой вершины.

Предположим орграф G={X, A} имеет n вершин и m дуг. X={x₁, x₂,..., x_n}. Пронумеруем дуги l₁, l₂,..., l_m.

Матрицей смежности орграфа G={X, A} c множеством вершин Х называется матрица В=b_ij (i=1, 2,..., n; j=1, 2,..., n), в которой элемент b_ij равен числу дуг вида (x_i, x_j), идущих от вершины x_i к вершине x_j.

Например, составим матрицу смежности для орграфа, представленного на рис.2.7

Рис.2.7

Составим 1-ю строку матрицы смежности:

b₁₁=0, т.к. при вершине х, нет петель;

b₁₂=2, т.к. из вершины х, выходят 2 дуги к х₂;

b₁₃=1, т.к. из х₁ выходит одна дуга к х₃;

b₁₄=0, т.к. нет дуг, выходящих к х₄.

Составим 2-ю строку:

b₂₁=0, т.к. из х₂ к х₁ нет дуг;

b₂₂=1, т.к. при вершине х₂ есть одна петля;

b₂₃=1, т.к. одна дуга выходит из х₂ к х₃ и т.д. Получим

Матрица смежности полностью определяет орграф.

Заметим, что матрица смежности орграфа в общем случае не является симметрической. А матрица смежности неориентированного графа есть симметрическая матрица.

Матрицей инциндентности орграфа G={X, A} c множеством вершин X={x₁, x₂,..., x_n} и множеством дуг A={l₁, l₂,..., l_m} матрица C=C_ij размера nm, у которой

Каждый столбец этой матрицы имеет один элемент +1 и один элемент -1, а все остальные элементы столбца равны 0.

Например, составим матрицу инцидентности для орграфа представленную на рис.2.7

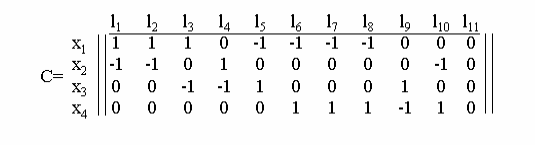
Петле l₁₁ соответствует нулевой столбец. Матрица инцидентности только указывает на наличие петель в орграфе, но не указывает, каким вершинам эти инцидентны.

Если орграф C_ij одновременно равен +1 и -1, что приводит к неоднозначности элементов матрицы С.

Для задания графа с петлями «расщепим» матрицу С на две матрицы С⁺ и С^-

Если граф без петель, то С=С⁺ - С^-.

Для графа, представленного на рис.2.7 составим матрицы смежности С⁺ (начала дуг) и С^- (конца дуг).

Если одну матрицу наложить на вторую, то там, где единицы совпадают, это соответствует петле; петля находиться в вершине х₂.

3. Путь и контур

Последовательность дуг ориентированного графа называется путем, если конец предыдущей дуги является началом следующей дуги. Так, например в орграфе на рис.2.8 последовательность дуг: (х₁, х₂), (х₂, х₅), (х₅, х₄), (х₄, х₃) является путем из вершины х₁ в вершину х₃.

Рис.2.8

Число дуг, образующих путь, называется длиной пути.

Путь называется составным, если в нем повторяется хотя бы одна дуга, сложным, если в нем повторяется хотя бы одна вершина, и простым - в противном случае.

Контуром называется путь начальная и конечная вершины которого совпадают. Так последовательность дуг: (х₂, х₅), (х₅, х₄), (х₄, х₃), (х₃, х₂) является контуром.

Число дуг. образующих контур, называется длиной контура. Петля - это контур единичной длины.

Таким образом, для орграфа введены понятия:

дуга, путь, контур, а для неориентированного графа аналогичные понятия:

ребро, цепь, цикл.

Пример. Из лагеря вышли 5 туристов: Василий, Галина, Анатолий, Елена и Михаил. Анатолий идет впереди Михаила, Елена - впереди Василия, но позади Михаила, Галина впереди Анатолия. Кто идет первым и кто последним?

Решение. Попробуем решить построением орграфа отношения :’x идет сзади y’.

Рис.2.15

На плоскости отметим 5 точек, которые обозначим первыми буквами имен туристов (рис.2.15). От x проведем стрелку к y.

По тексту МА, ВЕ, ЕМ, АГ, проводим стрелки и получим орграф. Первой идет Галина, а последним - Василий.