10. Хроматическое число графа.

Другой характеристикой графа G является хроматическое число, связанное с раскрашиванием графа.

Раскрашиванием графа называют процесс сопоставления его вершин цветов, при котором любые две соседние (смежные) вершины оказываются разноцветными. Минимальное число цветов, необходимых для такой раскраски графа, называют хроматическим.

Хроматическое число связано с раскрашиванием карт. Пусть дана географическая карта. Требуется окрасить каждое государство так, чтобы любые два государства, граничащие между собой, были окрашены в разные цвета. Если в нашем распоряжении имеется достаточное количество различных красок, то это не составит никакого труда. Намного сложнее решить вопрос о наименьшем количестве красок, достаточном для такого раскрашивания. Эта проблема была очень популярна в прошлом столетии, ею занимались известные математики.

Доказана теорема о пяти красках. Любой плоский граф можно раскрасить пятью красками.

Также удалось доказать, что с помощью четырех красок можно осуществить правильную раскраску для плоских графов с числом вершин не превосходящих 38.

В терминах графов задача может быть поставлена следующим образом. Дан произвольный плоский граф G без петель. Имея некоторое количество красок  необходимо раскрасить каждую вершину одной из этих красок так, чтобы любые две смежные вершины имели различную окраску. Если граф G является  раскрашиваемым, но не является (-1)- раскрашиваемым, то называют его  - хроматическим, а число  называют хроматическим числом графа G и обозначают (G)=.

Рис.1.29

На рис.1.29 изображен 4-хроматический граф. Цвета обозначены греческими буквами , , , .

§2. Ориентированные графы

1. Понятие об ориентированном графе

В §1, введя понятие о графе, мы рассматривали в качестве примера состязания футбольных команд A, B, C, D, E, F. Все команды по одному разу должны встретиться между собой. Команды уже игравшие соединим ребрами, и таким образом, получили неориентированный граф (рис.2.1).

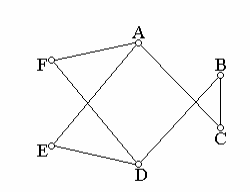
Рис.2.1

Однако такой граф не дает ответа на вопрос: кто именно выиграл эту игру? Этот недостаток может быть устранен. Если команда А выиграла у команды С, условимся ставить на ребре АС стрелку, направленную от А к С. Предположим, что нам известны результаты всех уже сыгранных игр (ничейные результаты исключены) и вдобавок к графу рис.2.1 соответствующие стрелки, пусть при этом получиться граф, изображенный на рис.2.2.

Рис.2.2

На это графе показано, что команда А выиграла у команд С и F, но проиграла команде Е; команда В выиграла у команд С и D; а команда D проиграла командам В, Е, F, и т.д. Граф, на котором указано направление каждого его ребра, называется ориентированным графом (сокращенно орграф).

Если же ничейные результаты неизбежны, можем отразить их на графе, оставляя соответствующие ребра неориентированными. При это получиться так называемый смешанный граф, на котором имеются как ориентированные, так и неориентированные ребра.

План транспортных магистралей города дает нам несколько специальный, но зато наглядный пример графа. На современном плане города должны быть показаны не только относительное расположение улиц и их пересечений, так же и то, на каких улицах имеется двусторонний поток транспорта, а на каких - одностороннее движение, причем в последнем случае должно быть показано направление движения. На улицах с двусторонним движением неориентированное ребро можно заменить двумя ориентированными ребрами, соединяющими те же самые вершины А и В и имеющими противоположные направления (рис.2.3).

Рис.2.3

Математически неориентированный граф G определяется двумя множествами: X={x₁, x₂, ..., x_n} - конечное множество вершин, А - конечное множество дуг (х_i, x_j), соеденяющих между собой все или часть вершин. Каждая дуга (x|_i, x_j) задается упорядоченной парой вершин x_i, x_j, т.е. дуга выходит из вершины x_i и входит в вершину x_j. Дуга (x_i, x_j) называется ориентированной, при этом вершина x_i называется начальной, а x_j - конечной вершиной.

Формально ориентированный граф G={X, A} определяется как множество вершин Х и множество А ориентированных дуг. Ориентированный граф будем называть кратко орграф. Дуга (x_i, x_j) с концами в одной и той же вершине называется петлей. Граф, у которого нет петель, называется графом без петель. На рис.2.4 представлен орграф G={X, A}, где X={x₁, x₂, x₃}, A={(x₁, x₁), (x₁, x₂), (x₁, x₃), (x₃, x₂)}.

Рис.2.4