8. Деревья и лес

Деревом называется связный граф, не содержащий простых циклов. Такой граф, в частности, не имеет и кратных ребер.

Рис.1.24

Из определения дерева вытекает также, что для каждой пары его вершин существует его единственная соеденяющая их цепь.

Деревья имеют многочисленные применения. Упомянем лишь один. Граф, приведенный на рис.1.24, может представлять процесс сортировки писем на главпочтамте. Первоначально пачка писем поступает на главпочтамт (х₀), там почта дробиться на три района х₁, х₂, х₃, на районных почтовых отделениях снова дробиться по почтовым отделениям и т.д.

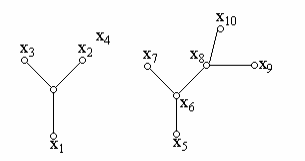
Рис.1.25

Если граф не связный, не содержит циклов, то каждая его связная компонента будет деревом (рис.1.25). Пользуясь терминологией, принятой в ботанике такой граф можно назвать лесом.

Итак, произвольный граф. Не содержащий циклов называется лесом, а его связные компоненты называются деревом.

Простейшее дерево имеет только одно ребро и две вершины. Если мы добавим еще одно ребро, то прибавляется также и вершина, следовательно, справедлива теорема.

Теорема:

Дерево с n вершинами имеет n-1 ребер.

Вместо одного дерева рассмотрим теперь лес, состоящий из К связных компонент, каждая из которых является деревом (рис.1.26).

Рис.1.26

Для каждой из компонент число ребер на единицу меньше числа вершин. Следовательно, справедлива теорема.

Теорема:

Лес, состоящий из К компонент и имеющий n вершин, содержит n-k ребер.

В следующей теореме перечислены некоторые простые свойства деревьев.

Теорема:

Пусть граф G имеет n вершин. Тогда следующие утверждения эквивалентны:

1. G является деревом;

2. G не содержит циклов и имеет (n-1) ребер;

3. G связан и имеет (n-1) ребер;

4. любые две вершины графа G соединены только простой цепью;

5. G не содержит циклов. Но добавляя к нему только одно новое ребро, получим ровно один цикл;

6. G связен и каждое его ребро является мостом.

Поясним последнее свойство.

Рассмотрим произвольный граф, представленный на рис.1.27. Пусть х- некоторое ребро графа G, граф G - х получается путем удаления из G ребра х (обе концевые вершины в графе остаются).

Рис.1.27

Ребро х графа G={X, A} называется мостом или разделяющим ребром, если связность G-x больше связности G. На рис.1.27 связность графа G равна 1, а связность графа G-x равна 2, следовательно, ребро х является мостом.

Очевидно, удаление любого ребра из дерева делает его несвязным.

9. Цикломатическое число графа

Пусть дан произвольный связный граф G={X, A}.

Для него можно составить остовные подграфы G₁={X, A₁}, G₂={X, A₂}, ..., G={X, A_k}. (Оставный подграф имеет тоже множество вершин, что и граф G, а множество ребер A_yA). Среди остовных подграфов могут быть и деревья.

Дерево, являющееся остовным подграфом графа G, называется остовным деревом или остовом.

Например: Дан граф G={X, A}, где X={x₁, x₂, x₃, x₄, x₅}.

Рис.1.28

На рис.1.28 изображен граф G и его два остова б), в).

Можно привести и другие варианты остовных деревьев.

Теорема:

В связном графе всегда существует остовное дерево.

Доказательство:

Если в графе нет циклов, то он является деревом и, следовательно, сам себя покрывает. При наличии циклов исключим из графа ребра, образующие циклы, (рис.1.28) и придем к подграфу, не содержащему циклов. Этот подграф и будет остовным деревом.

Пусть произвольный связный граф имеет n вершин и m ребер. Все остовные деревья будут иметь n вершин и (n-1) ребер. А теперь легко подсчитать, сколько ребер нам пришлось удалить.

Определение:

Число удаленных ребер в процедуре образования остовного дерева называется цикломатическим числом (циклическим рангом) и обозначается (G).

(G)=m-(n-1)=m-n+1;

Цикломатическое число определяет меру связности графа. На рис.1.28 (G)=3.

Очевидно, цикломатическое число графа является целым неотрицательным числом. Граф является деревом тогда и только тогда, когда его цикломатическое число равно 0.

Если граф содержит К компонент связности, то его цикломатическое число

(G)=m-(n-k)=m-n+k.