Эйлеровы и гамильтоновы графы
Первая работа о графах, принадлежащая швейцарскому математику Леонарду Эйлеру (1707 - 1783), появилась в 1736 г. в публикациях Петербургской Академии наук. В 1727 г., когда ему едва исполнилось 20 лет, он был приглашен в Российскую Академию наук. Он добился блестящих успехов в математике, физике, астрономии; написал огромное количество работ. К тому времени, когда он написал работу о графах, он потерял зрение на один глаз, а к старости совершенно ослеп, но даже это не остановило потока его работ.
Эйлер начал свою работу о графах с рассмотрения одной головоломки - так называемой задачи о «Кенигсбергских мостах». Город Кенигсберг (ныне Калининград) расположен на берегах реки Прегель (Преголи) и двух островах. Различные части города были соединены семью мостами (рис.1.20)
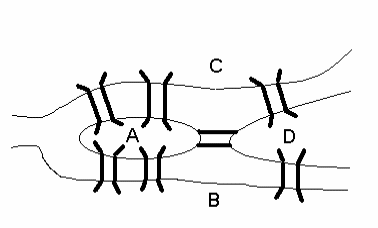
Рис.1.20
По воскресеньям горожане совершали прогулки по городу. Вопрос заключался в том, можно ли совершить прогулку таким образом, чтобы, выйдя из дома, вернуться обратно пройдя в точности один раз по каждому мосту?
Схематически карта изображена на рис.1.20.
Четыре части города обозначены буквами А, В, С, D.
Так как нас интересует только переходы по мостам мы можем считать А, В, С, D вершинами некоторого графа, ребра которого отвечают соответствующим мостам. Этот граф изображен на рис.1.21
Рис.1.21
Эйлер показал, что этот граф не представляет собой единого цикла; иными словами, с какой бы вершины ни начали обход, не сможем обойти весь граф и вернуться обратно, не проходя никакого ребра дважды.
Ведь если такой цикл существовал, то в каждой вершине графа было бы столько же входящих в нее ребер, сколько и выходящих из нее, т.е. в каждой вершине графа было бы четное число ребер. Однако это условие не выполнено для графа, представленного на рис.1.21.
Цикл называется эйлеровым, если каждое ребро графа участвует в его образовании один раз. Граф, содержащий такой цикл, называется эйлеровым.
Возникает вопрос: можно ли найти необходимые и достаточные условия для того, чтобы граф был эйлеровым. Ответ дает теорема.
Теорема:
Граф G={X, A} является эйлеровым тогда и только тогда, когда он связан и степень каждой вершины (хi) - четное число.
Итак, эйлеров граф представляет собой единый цикл, каждое ребро его участвует один раз в цикле, при этом одна и та же вершина может быть пройдена несколько раз.
Эйлеровым графом должен был быть и план любой выставки: вдоль ее помещений можно было бы расставить знаки, показывающие, как именно посетители должны двигаться, чтобы осмотреть каждый экспонат в точности по одному разу. Эйлеров граф можно нарисовать не отрывая карандаша от бумаги и не проводя никакого ребра дважды. Для эйлерова графа выполнение такого рисунка начинается и заканчивается в одной и той же вершине.
В 1859 г. известный ирландский математик сэр Уильям Роуэн Гамильтон выпустил в продажу головоломку. Ее основной частью был правильный додекаэдр, его гранями служат 12 правильных пятиугольников, причем в каждой из 20 его вершин сходиться по три ребра. Каждая вершина помечена названием одного из крупных городов. Задача состояла в нахождении пути вдоль ребер, проходящего через каждый город в точности по одному разу. Гамильтоновой линией на графе называется цикл, проходящий через каждую вершину графа в точности по одному разу. Он не показывает, вообще говоря, всех ребер; ведь в каждой вершине он проходит в точности по двум ребрам. Как видим, имеется аналогия между эйлервыми и гамильтоновыми линиями. Первая проходит один раз по каждому ребру, вторая - через каждую вершину.
Итак, цикл называется гамильтоновым, если каждая вершина графа участвует в его образовании только один раз. Граф, содержащий такой цикл называется гамильтоновым. Граф, который содержит простую цепь, проходящую через его вершину, называется полугамильтоновым. На рис.1.23 изображены соответственно негамильтонов, полугамильтонов и гамильтонов графы.
Рис.1.23