2. Задание графов с помощью матриц.

Для задания графов существует несколько матриц, основные из которых матрицы смежности и инцидентности.

Предположим граф G={X, A} имеет n вершин и m ребер, где конечное множество вершин - Х={х₁, х₂, ..., х_n} и множество ребер А={l₁, l₂, l₃, ..., l_m}.

Матрицей инцидентности графа G называется матрица R=r_ij размера nхm, у которой элементы

Принято, петле соответствует нулевой столбец. Матрица инцидентности только указывает на наличие петель в графе, но не указывает, каким вершинам эти петли инцидентны.

Например, для графа, изображенного на рис.1.9 имеем матрицу инцидентности R

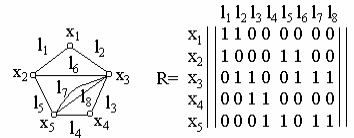
Рис.1.9

Заполнить матрицу удобнее по столбцам.

Каждый столбец матрицы имеет два элемента 1, остальные - 0. Элемент 1 ставиться в строках, соответствующих вершинам, которые соединяют это ребро.

Матрица смежности графа G называется матрица Q=q_ij размера nn, в который элемент q_ij равен числу ребер в G, соединяющих вершину х_i с вершиной х_j. Матрица смежности Q является симметрической, т.е. q_ij=q_ji.

Для графа, изображенного на рис.1.9 матрица смежности имеет вид.

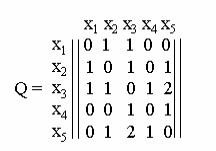
Матрица смежности полностью определяет граф.

Пример. Задана симметричная матрица неотрицательных целых чисел. Нарисовать на плоскости граф G, имеющий заданную матрицу Q своей матрицей смежности. Найти матрицу инцидентности R графа G.

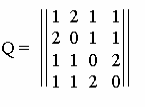
Решение Построим граф по заданной матрице смежности Q.

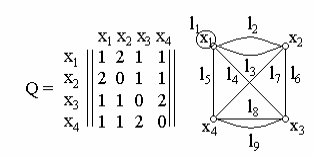
Рис.1.10

Теперь найдем матрицу инцидентности графа G

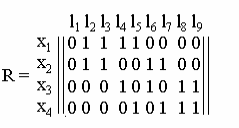
Петле соответствует нулевой столбец. Ребро (х₁, х₂) имеет кратность 2, поэтому ребра l₂ и l₃ имеют одинаковые столбцы, аналогично и столбцы l₈ и l₉ одинаковые.

Решение закончено.

Построенный граф G на рис.1.10 может выглядеть и иначе (рис 1.11 а и б)

а) G₁ б) G₂

Рис.1.11

Очевидно, что графы, которые могут быть изображены различным образом, могут соответствовать одним и тем же элементам некоторой системы и выражать одни и те же отношения.

3. Изоморфные графы

Заметим, что один и тот же G (рис.1.10, 1.11) можно изображать по разному.

Во-первых, совсем не обязательно изображать его ребра прямолинейными. Можно провести любые линии, соединяющие те же самые вершины, что и раньше.

Во-вторых, можно произвольно располагать вершины на плоскости.

Однако установить эквивалентность двух графов иногда очень сложно.

Определение:

Два графа, между вершинами и ребрами которых можно установить взаимно однозначное соответствие с сохранением смежности, называется изоморфными.

Операция замены графа G на изоморфный ему граф G₁ представляет деформацию графа G без разрезания ребер. Например, графы G₁ и G₂ рис.1.12 изоморфны,

G₁ G₂

Рис.1.12

так как граф G₂ можно получить из графа G₁ путем деформации этого графа без разрезания ребер (вершину х₄ переместим во внутрь треугольника, при этом ребра деформируются).

Между вершинами и ребрами этих графов можно установить взаимно однозначное соответствие, сохраняющее смежность.

Нередко приходиться решать вопрос о том, являются ли два данных графа изоморфными. Иногда это сразу ясно, что это не так. Не могут быть изоморфными графы, имеющие разное число вершин и неодинаковое число ребер.

Пример:

Изоморфны или нет следующие пары графов ?

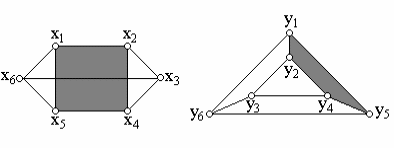
x₁y₁, x₂y₂, x₃y₃, x₄y₄, x₅y₅, x₆y₆.

Соответствие вершин установлено, проверим смежность вершин:

x1x2, x5, x6;	y1y2, y5, y6;
x2x1, x4, x3;	y2y1, y4, y3;
x3x2, x4, x6;	y3y2, y4, y6;
x4x2, x3, x5;	y4y2, y3, y5;
x5x1, x4, x6;	y5y1, y4, y6;
x6x1, x3, x5;	y6y1, y3, y5;

Смежность вершин сохранена. Следовательно, эти графы изоморфны.