§3. Оптимизационные задачи на графах

1. Построение остовного дерева минимальной длины. Алгоритм Краскала построения минимального дерева.

Большое практическое значение имеет следующая задача, которую можно сформулировать в виде задачи о проведении дорог.

Представим, нужно построить сеть железных дорог, которые соединили бы n данных городов, причем так чтобы пассажир мог проехать из каждого города в любой другой. Для каждой пары городов известна стоимость (х, у) строительства соединяющей их дороги.

Задача состоит в том, чтобы построить самую короткую из всех возможных дорог. Называя в графе, изображающем сеть дорог, величину (х, у) длиной ребра, соединяющего города х и у, приходим к задаче о построении графа наименьшей длины.

Ясен, что граф, вершины которого соответствуют городам, а ребра - соединяющим их железным дорогам, должен быть деревом. Задача состоит в нахождении алгоритма, определяющего, какое из возможных n^n-2 деревьев, соединяющих эти города, будет наименьшей длины.

Алгоритм, известный под названием алгоритма Краскала, дает следующая теорема.

Теорема:

Пусть G - связный граф с n вершинами. Тогда следующая процедура приводит к остовному дереву наименьшей длины:

1. выберем ребро ₁, обладающее в G наименьшей длиной;

2. определим по индукции последовательность ребер ₁, ₂,..., _n-1, выбирая на каждом шаге ребро с наименьшей мерой, обладающее тем свойством, что подграф Т графа G, ребрами которого являются ₁, ₂,...,_n-1, и есть требуемое остовное дерево.

Пример. Расстояние между городами A, B, C, D, E, F в сотнях километрах дано в таблице.

Требуется построить сеть железных дорог так, чтобы количество затраченных рельсов было минимальным и пассажир мог из каждого города проехать в любой другой город.

Решение. Построим граф G с 6 вершинами, соответствующим 6 городам A, B, C, D, E, F.

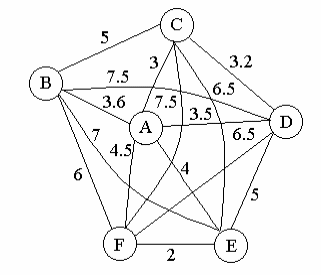
Рис.3.1

Соединим каждую вершину со всеми остальными. Получим полный граф G=K₆.

Число ребер полного графа m=1/2n(n-1)=1/265=15

На каждом ребре графа (согласно таблице) проставим расстояние между соответствующими городами (рис.3.1). Эту цифру называют мерой (весом) соответствующего ребра, например. (С, D)=3.2

Теперь наша задача будет состоять в определении одного из возможных n^n-2=6^6-2=6⁴=1296 деревьев, соединяющих данные города. Это остовное дерево Т должно иметь наименьшую сумму мер его ребер (сумма берется по всем ребрам дерева Т).

Число ребер в исходном дереве Т можно определить, зная цикломатическое число графа G=K₆. Цикломатическое число графа

(G)=m-n+k,

где m-число ребер, n-число вершин; k-число компонент связности графа.

Для данного графа m=15, n=6, k=1.

(G)=15-6+1=10;

Следовательно, в графе нужно убрать 10 ребер, чтобы получить остовное дерево, которое будет иметь 15-10=5 ребер.

Для того, чтобы построить для графа G остовное дерево Т наименьшей длины, воспользуемся алгоритмом Краскала, который сформулирован в теореме.

1. Выбираем ребро наименьшей длины: (EF)=2.

2. Выбираем ребро, у которого наименьшая длина. Это ребро АС, (АС)=3 (рис.3.2).

Рис.3.2

3. Выбираем из оставшихся 13 ребер ребро наименьшей длины. Это ребро CD, (CD)=3.2.

4. Из оставшихся 12 ребер выбираем ребро с наименьшей длиной при условии, что оно не образует цикла (исключим из рассмотрения ребро AD). Это ребро ВА, (ВА)=3.6.

5. Исключим из рассмотрения ребра ВС и АD, образующие циклы. Из оставшихся ребер наименьшую длину имеет ребро АЕ, (АЕ)=4.

Алгоритм закончен. На графе (рис.3.2) приведено остовное дерево Т. Длина остова Т:

(FE)(AE)(AB)(AC)(CD)=2+4+3.6+3+3.2=15.8