30

Графы Предмет теории графов

Первая работа по теории графов, принадлежащая известному швейцарскому математику Л.Эйлеру, появилась в 1736г. Вначале теория графов казалась довольно незнеачительным разделом математики, т.к. она имела дело в основном с математическими развлечениями и головоломками. Однако дальнейшее развитие математики особенно ее приложений дало сильный толчок развитию теории графов. Уже в XIX столетии графы использовались при построении схем электрических цепей и молекулярных схем. В настоящее время теория графов проедставляет собой раздел математики, имеющий широкое практическое значение. Можно указать и главы чистой математики, например, теория математических отношений, в которых теория графов служит естественным аппаратом; с другой стороны, эта теория находит многочисленные применения в разнообразных практических вопросах; при решении транспортных задач, задач о потоках в сети нефтепроводов; применяется в экономике, психологии, биологии; при проектировании интегральных схем и схем управления, при исследовании автоматов, логических цепей, блок-схем программ, в электротехнике, для анализа сетей связи. Математические развлечения и головоломки тоже остаются частью теории графов, особенно если отнести к ним знаменитую проблему четырех красок.

(Каждая географическая карта может быть раскрашена с соблюдением условия, чтобы страны с общей границей были раскрашены в разные цвета, при помощи четырех красок).

§1 Неориентированные графы

1. Понятие о графе

Предположим, проводятся соревнования по футболу.

Пусть общее число команд равно шести, обозначим их буквами A, B, C, D, E, F. Все команды по одному разу должны встретиться между собой. Один из вариантов схемы встреч можно изобразить так. Каждую команду представим точкой или маленьким кружочком и соединим отрезком те пары точек, которые соответствуют командам, уже игравшим друг с другом (рис.1.1).

Схема такого вида называется графом. Она состоит из нескольких точек A, B, C, D, E, F, называемыми вершинами, и нескольких соединяющих эти точки отрезков, таких, как АС, ВС, FD и т.д., называемых ребрами графа.

До начала соревнований, пока никакие игры не проводились, на графе нет никаких ребер. Такой граф состоит из одних изолированных вершин, т.е. из вершин, не соединенных никакими ребрами. Граф такого вида мы будем называть нуль-графом (рис.1.2).

Рассмотрим другой крайний случай. Предположим, что каждая команда сыграла по одному разу с каждой из оставшихся команд. Тогда на соответствующем графе каждая пара вершин будет соединена ребром. Такой граф называется полным графом (рис.1.3).

Полный граф можно представить себе как n- угольник, в котором проведены все диагонали. На рис.1.4. приведены полные графы с числом вершин n=2, 3, 4, 5.

Имея некоторый граф, например G, изображенный на рис.1.1, мы всегда можем превратить его в полный граф с теми же самыми вершинами, добавив недостающие ребра (т.е. ребра, соответствующие играм, которые еще будут сыграны).На рис.1.5 мы сделали это для графа рис.1.1.

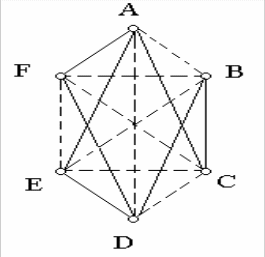
Еще не состоявшиеся игры изображены пунктиром. Можно такие отдельно начертить граф, соответствующий пока еще сыгранным, будущим играм (рис.1.6). Этот новый граф называют дополнением

графа G, обозначают G

Рис.1.5.

Ребра обоих графов G и G^` вместе составляют полный граф с теми же вершинами (рис.1.3, 1.5) .

Математически неориентированный граф (далее: граф) определяется двумя множествами G={X,A}, где Х-конечное множество вершин (точек) х₁, х₂, ...,х_n (Х_i є Х, i=1,2,...,n); A- некоторое множество ребер, соединяющих между собой все или часть этих вершин. Каждое ребро задается неупорядоченной парой вершин (x_i, x_j). Так как порядок вершин не играет роли, то наряду с записью (x_i, x_j) допустима и запись (x_j, x_i).

Рис. 7

Таким образом, граф G полностью задается и обозначается парой G={X, A}. На рис.7, имеется ребро, которое начинается и заканчивается в одной и той же вершине Х₁; такие ребра называются петлями. Некоторые пары различных вершин графа могут быть соединены несколькими ребрами, как это изображено на рис.7, такие графы называют графами с кратными ребрами. Вместо того чтобы проводить несколько ребер между одними и теми же вершинами Х₁ и Х₂ можно провести всего одно ребро, приписав ему кратность, показывающую сколько раз надо считать это ребро.

Граф называется простым, если любая пара вершин соединена не более чем одним ребром.

Две вершины называются смежными, если существует ребро, соединяющее их.

Два ребра называются смежными, если они имеют общую вершину.

Ребро (x_i, x_j) называется инцендентным каждой их вершин x_i и x_j и обратно. Вершина x_i (вершина х_j) инцидентна ребру (х_i, х_j).

Смежность является отношением между подобными элементами (между вершинами или между ребрами), тогда как инцидентность есть отношение между разнородными элементами (между вершиной и ребром).

Граф G={X, A} называется полным, если для любой пары вершин х_i и х_jєХ существует ребро (х_i, x_j)єA, то есть для каждой пары вершин существует по крайней мере одно ребро, соеденяюцее их. Иначе, граф, в котором любые две вершины смежны, называется полным. Полный граф с n вершинами обозначается через K_n. На рис.1.4 изображены графы К₂, К₃, К₄, и К₅ на рис.1.3 - граф К₆.