3. Функція розподілу Фермі – Дірака Ця функція визначається аналогічно функція розподілу Бозе – Ейнштейна і має такий вид:

,

де – середнє число частинок (ферміонів) в квантовому стані з енергією ; – хімічний потенціал, який, на відміну від хімічного потенціалу, що входить в функцію розподілу Бозе – Ейнштейна , може мати додатнє значення.

Якщо , то розподіли Бозе – Ейнштейна і Фермі — Дірака переходять в класичний розподіл Максвела – Больцмана:

,

де

.

Таким чином, при високих температурах обидва "квантованих" газа ведуть себе подібно класичному газу.

4. Поняття про виродження систем частинок, що описуються квантовими статистиками

Система частинок (зокрема, ідеальний газ) називається виродженою, якщо її властивості суттєво відрізняються від властивостей систем, що підкоряються законам класичної статистики. Відступ в поведінці бозе- і ферми-газів від класичного максвел-больцманівського газу називається виродженням газів (вироджений газ). Виродження газів стає істотним при дуже низьких температурах і великій густині.

Параметром виродження називається величина .

Температурою виродження називається температура, нижче за яку чітко проявляються квантові властивості ідеального газу, зумовлені тотожністю частинок, тобто – це температура, за якої виродження стає суттєвим. Якщо , то поведінка системи частинок (газу) описується класичними законами.

5. Поняття про виродження електронного газу в металах

Розподіл електронів по різних квантових станах підкоряється принципу Паулі, згідно з яким в одному стані не може бути двох однакових (з однаковим набором чотирьох квантових чисел) електронів; вони повинні відрізнятися якоюсь характеристикою, наприклад, напрямом спіну. Отже, по квантовій теорії, електрони в металі не можуть розташовуватися на найнижчому енергетичному рівні навіть при 0 К. Згідно з принципом Паулі, електрони вимушені підійматися вгору "по енергетичних сходах".

Електрони провідності в металі можна розглядати як ідеальний газ, що підкоряється розподілу Фермі – Дірака

,

Якщо – хімічний потенціал електронного газу при , то середнє число електронів в квантовому стані з енергією Е дорівнює

.

Для ферміонів (а електрони є ферміонами) середнє число частинок в квантовому стані і вірогідність заселеної квантового стану співпадають, оскільки квантовий стан або може бути не заселений, або в ньому знаходитиметься одна частинка. Це означає, що для ферміонів , де – функція розподілу електронів по станах.

З вище наведеної формули витікає, що при функція розподілу , якщо . Графік цієї функції наведено на рис. 27.1, а. В області енергій від 0 до функція дорівнює одиниці. При вона стрибкоподібно змінюється до нуля. Це означає, що при всі нижні квантові стани, аж до стану з енергією заповнені електронами, а всі стани з енергією, більшою за , вільні. Отже, є не що інше, як максимальна кінетична енергія, яку можуть мати електрони провідності в металі при . Ця максимальна кінетична енергія називається енергією Фермі і позначається . Тому розподіл Фермі – Дірака зазвичай записується у вигляді

.

Рис. 27.1

Найвищий енергетичний рівень, зайнятий електронами, називається рівнем Фермі. Рівню Фермі відповідає енергія Фермі , яку мають електрони на цьому рівні. Рівень Фермі, очевидно, буде тим вище, чим більше густина електронного газу. Роботу виходу електрона з металу потрібно відлічувати не від дна "потенціальної ями", як це робилося в класичній теорії, а від рівня Фермі, тобто від верхнього із зайнятих електронами енергетичних рівнів.

Для металів при не дуже високих температурах виконується нерівність . Це означає, що електронний газ в металах практично завжди знаходиться в стані сильного виродження. Температура виродження визначається з умови . Вона визначає межу, вище за яку квантові ефекти перестають бути істотними. Відповідні розрахунки показують, що для електронів в металі , тобто для всіх температур, при яких метал може існувати в твердому стані, електронний газ в металі вироджений.

При температурах, відмінних від 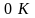, функція розподілу Фермі –Дірака плавно змінюється від 1 до 0 у вузькій області (порядку кТ) в околиці E_F (рис. 27.1, б). (Тут же для порівняння пунктиром наведено функцію розподілу при .) Це пояснюється тим, що при Т > 0 невелике число електронів з енергією, близькою до , збуджується унаслідок теплового руху і їх енергія стає більшою за . Поблизу межі Фермі при заповнення електронами менше одиниці, а при – більше нуля. В тепловому русі бере участь лише невелике число електронів, наприклад при кімнатній температурі і температурі виродження , — це 10^-5 від загального числа електронів.

Якщо ("хвіст" функції розподілу), то одиницею в знаменнику функції розподілу Фермі –Дірака можна знехтувати порівняно з експонентою і тоді розподіл Ферма — Дірака переходить в розподіл Максвела – Больцмана. Таким чином, при , тобто при великих значеннях енергії, до електронів в металі справджується класична статистика, в той же час, коли , для них можливо застосувати лише квантову статистику Фермі – Дірака.