Тема 3 графическое изображение статистических данных. Оценка концентрации изучаемого показателя.

3.1 Графические отображения статистических данных

Для наглядности вариационные ряды изображают графически в основном с помощью полигона (преимущественно дискретные ряды) и гистограммы (интервальные ряды).

Для построения полигона и гистограммы используется прямо­угольная система координат, на оси абсцисс которой строится шкала значений вариантов (или их интервалы), а на оси ординат — частот или частостей.

На рис. 1 показан полигон распределения 50 рабочих по тариф­ному разряду, построенный по данным задачи 2.1 для дискретного вариационного ряда.

Для интервального ряда строится гистограмма распределения. Она представляет собой ряд сомкнутых прямоугольников, основа­нием которых служит величина интервалов значений х_;, а высо­той — частота или частость.

На рис. 2 представлена гистограмма, построенная по данным задачи 2.2 для интервального вариационного ряда с равными ин­тервалами.

В случае неравных интервалов в качестве высоты прямо­угольников принимается плотность распределения — частное от деления частоты или частости каждого интервала на его величину

Соответственно и плотность распределения будет абсолютной или относительной.

На рис. 3 изображена гистограмма распределения, построенная по данным последней таблицы с учетом относительных плотностей распределения. (Величину первого интервала принимаем за 1, т.е. 0,5—1,5, последнего — за 4, т.е. 12—16.)

По накопленным частотам (частостям) строятся кумулята и огива распределения.

Для построения кумуляты из верхней границы каждого интервала на оси абсцисс восстанавливаются перпендикуляры, соответ­ствующие по высоте накопленной частоте (F_i}) или частости (р_i) с начала ряда по данный интервал, а затем последовательно (плавно) соединяются вершины перпендикуляров. Полученная кривая именуется кумулятой. Она отражает характер нарастания частот (или частостей) от группы к группе.

На рис. 4 представлена кумулята распределения 50 заводов по стоимости основных фондов, а на рис. 5 — кумулята распределения населения РФ по среднедушевым доходам в месяц в I полугодии 2006 г.

Если оси поменять местами, т.е. варианты откладывать на оси ординат, а накопленные частоты (или частости) — на оси абсцисс, то построенная аналогично по накопленным частотам кривая име­нуется огивой (рис. 6).

3.2 Диаграммы

Показанные выше графические изображения статистических данных называют часто диаграммами. При этом выделяют простые и сложные столбиковые диаграммы, ленточные, секторные, линейные, круговые, квадратные и т.п. Однако, с точки зрения содержания статистической информации все эти графические образы характеризуют ряды распределения и плотности распределения (полигоны и гистограммы), кумуляты или огивы.

Например.

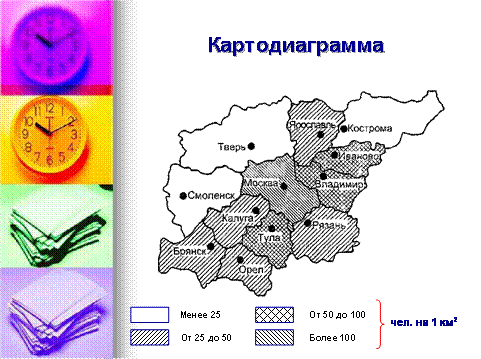
Особым случаем можно считать картодиаграммы, на которых характеристики измерений накладываются на картографический образ территории.