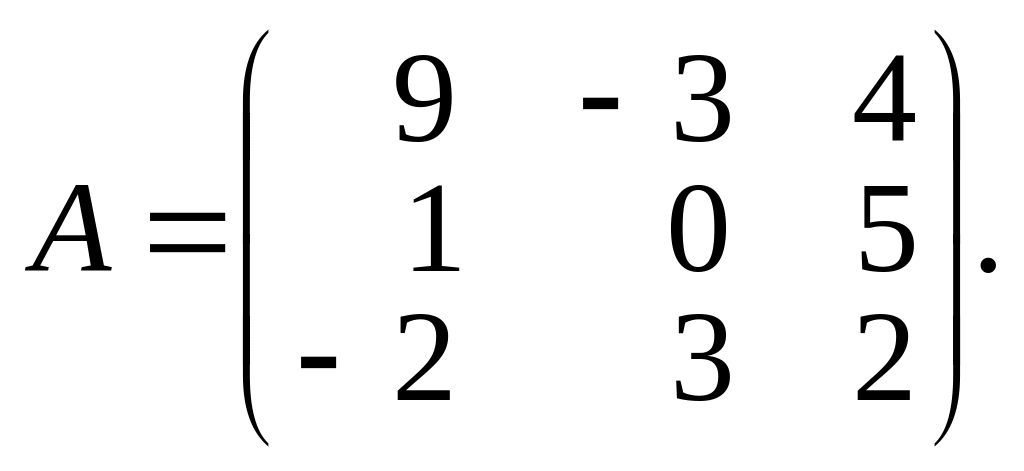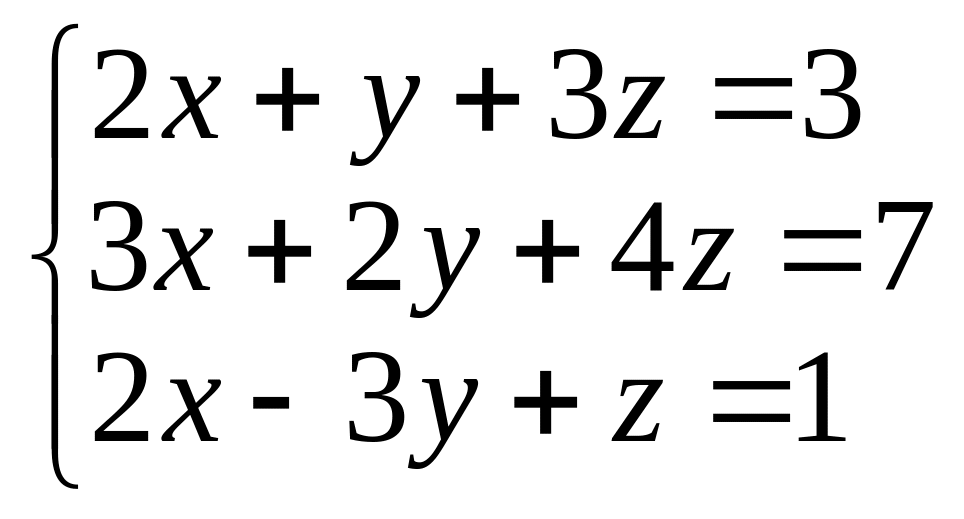- •Методические указания по выполнению контрольной работы и варианты контрольных работ
- •Варианты контрольных работ Контрольная работа 1 Тема 1. Матрицы и определители
- •Тема 2. Системы линейных уравнений
- •Тема 3–4. Векторная алгебра. Уравнение прямой
- •Тема 4. Уравнение плоскости
- •Тема 5. Линии второго порядка
- •Тема 13. Функции нескольких переменных
- •Тема 15. Решение дифференциальных уравнений
- •Тесты для промежуточного контроля знаний
Варианты контрольных работ Контрольная работа 1 Тема 1. Матрицы и определители
1.1. Вычислить определитель.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
1.2. Найти обратную матрицу для матрицы А и сделать проверку.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
Тема 2. Системы линейных уравнений
Решить систему уравнений тремя способами: методом обратной матрицы, методом Гаусса или методом Жордана–Гаусса.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
Тема 3–4. Векторная алгебра. Уравнение прямой
По координатам вершин треугольника ABC найти: периметр треугольника; уравнения сторон AB и BC; уравнение высоты AD; угол ABC; площадь треугольника. Сделать чертеж.
1. А(1; 2); В (–1; 2); С(3; 0).
2. А(3; 3); В(–3; –3); С(3; 5).
3. А(–1; 1); В(5; 1); С(3; 7).
4. А(3; 1); В (3; –5); С(–1; –1).
5. А(0; 5); В(5; 0); С(9; 3).
6. А(0; 0); В (8; 2); С(–2; 6).
7. А(–1; 4) В(–1; 2); С(–7; 3).
8. А(2; –1); В(5; 3); С(5; –2).
9. А(3; –3); В(7; –3); С(5; 5).
10. А(9; 0); В(5; 5); С(0; 3).
Тема 4. Уравнение плоскости
Даны точки М1 и М2.
Составить
уравнение плоскости, проходящей через
точку ш1 перпендикулярно вектору
![]()
Найти отрезки, отсекаемые данной плоскостью на осях координат. Начертить эту плоскость.
1. М1 (–3; 2; 1); М2 (1; 2; 3).
2. М1 (2; –1; 3); М2 (1; 3; 1).
3. М1 (5; –4; 1); М2 (3; 2; 1).
4. М1 (–2; 3; 1); М2 (1; 1; 4).
5. М1 (–1; 4; 3); М2 (2; 5; 1).
6. М1 (2; –1; 5); М2 (–2; 1; 3).
7. М1 (3; 2; –2); М2 (5; 1; 2).
8. М1 (2; –5; 4); М2 (1; 3; 4).
9. М1 (2; 2; –1); М2 (1; 3; 1).
10. М1 (4; –2; 1); М2 (3; 1; 2).
Тема 5. Линии второго порядка
Составьте уравнение окружности с центром в заданной точке А и данным радиусом R. Сделать чертеж.
1. А(1; –7); R = 1.
2. А(–2; 6); R = 2.
3. А(–3; 2); R = 3.
Найти координаты вершин, оси, фокусы и эксцентриситет эллипса. Сделать чертеж.
4. 16x2 + 25y2 = 400.
5. 4x2 + 9y2 = 36.
6. 9x2 + 16y2 = 144.
По заданному уравнению гиперболы найти: координаты вершин, координаты фокусов, эксцентриситет, уравнение асимптот. Сделать чертеж.
7. 4x2 – 5y2 – 100 = 0.
8. 9x2 – 4y2 – 144 = 0.
Показать, что уравнение представляет собой уравнение параболы, найти: вершину, ось, директрису параболы.
9. 4x2 + 4x – 8y – 19 = 0.
10. 2x2 + 6x + y + 4 = 0.
Тема 6. Пределы функций
Вычислить пределы.
1.
а)
![]() б)
б)
![]() в)
в)
![]()
2.
а)
![]() б)
б)
![]() в)
в)
![]()
3.
а)
![]() б)
б)
![]() в)
в)
![]()
4.
а)
![]() б)
б)
![]() в)
в)
![]()
5.
а)
![]() б)
б)
![]() в)
в)
![]()
6.
а)
![]() б)
б)
![]() в)
в)
![]()
7.
а)
![]() б)
б)
![]() в)
в)
![]()
8.
а)
![]() б)
б)
 в)
в)
9.
а)
![]() б)
б)
![]() в)
в)
![]()
10.
а)
![]() б)
б)
![]() в)
в)
Тема 7. Основы дифференцирования
Найти производную сложной функции.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
Тема 8. Исследование функций
Исследовать функцию и построить ее график.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
Контрольная работа 2
Тема 9. Неопределенный интеграл
Вычислить неопределенный интеграл.
1.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
2.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)![]() .
.
3.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
4.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
5.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
6.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)![]() .
.
7.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
8.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
9.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
10.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Тема 10. Определенный интеграл
10.1. Вычислить определенный интеграл.
1.
а)
![]() ;
б)
;
б)
![]() .
.
2.
а)
 ;
б)
;
б)
![]() .
.
3.
а)
![]() ;
б)
;
б)
![]() .
.
4.
а)
![]() ;
б)
;
б)
![]() .
.
5.
а)
![]() ;
б)
;
б)
![]() .
.
6.
а)
![]() ;
б)
;
б)
![]() .
.
7.
а)
![]() ;
б)
;
б)![]() .
.
8.
а)
![]() ;
б)
;
б)
![]() .
.
9.
а)
![]() ;
б)
;
б)
![]() .
.
10.
а)
![]() ;
б)
;
б)
![]() .
.
10.2. Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
Тема 11. Несобственный интеграл
Вычислить интеграл или установить его расходимость.
1.
а)
![]() ;
б)
;
б)
![]() .
.
2.
а)
![]() ;
б)
;
б)
![]() .
.
3.
а)
![]() б)
б)
![]()
4.
а)
 ;
б)
;
б)
![]() .
.
5.
а)
![]() ;
б)
;
б)
![]() .
.
6.
а)
![]() ;
б)
;
б)
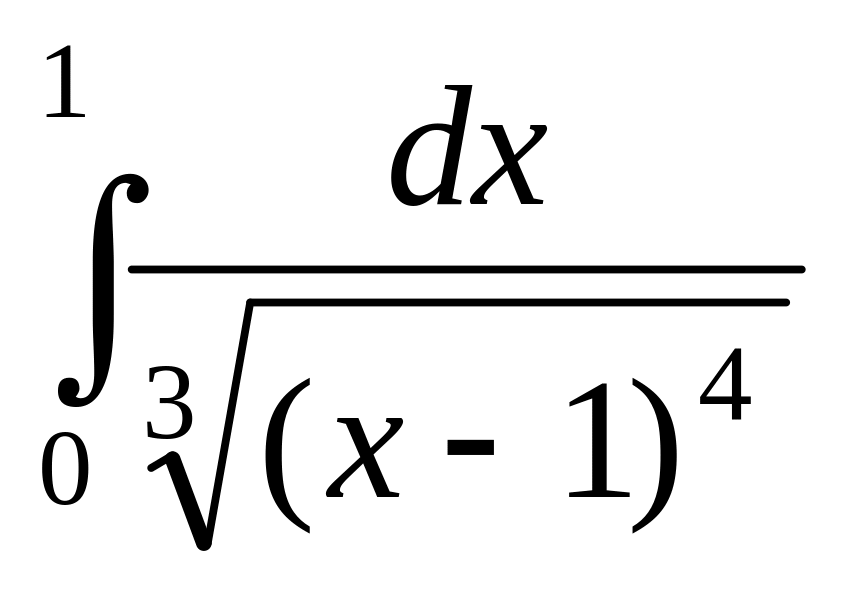 .
.
7.
а)
![]() ;
б)
;
б)
![]() .
.
8.
а)
![]() ;
б)
;
б)
![]() .
.
9.
а)
![]() ;
б)
;
б)
 .
.
10.
а)
![]() ;
б)
;
б)
![]() .
.
Тема 12. Ряды
12.1. Числовые ряды. Исследовать ряд на сходимость.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
12.2. Степенные ряды. Определить область сходимости степенного ряда.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|