5.5. Нарощення й дисконтування грошових потоків

Оскільки процес інвестування, як правило, має більшу тривалість у практиці аналізу ефективності капітальних вкладень, звичайно доводиться мати справа не з одиничними грошовими сумами, а з потоками коштів.

Обчислення нарощеної й дисконтованої оцінок сум коштів у цьому випадку здійснюється шляхом використання відповідних формул (5.1) і (5.2) для кожного елемента грошового потоку.

Грошовий потік прийнятий зображувати на тимчасовій лінії в одному із двох способів:

А.

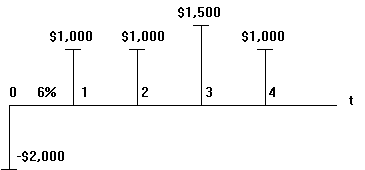
В.

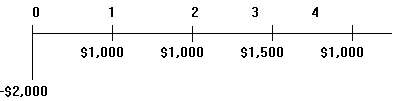
Представлений на малюнку грошовий потік полягає в наступному: у цей час виплачується (знак "мінус") $2,000, у перший і другий роки отримане $1,000, у третій - $1,500, у четвертий - знову $1,000.

Елемент грошового потоку прийнято позначати CFk (від Cash Flow), де k - номер періоду, у який розглядається грошовий потік. Дійсне значення грошового потоку позначене PV ( Present Value), а майбутнє значення - FV ( Future Value).

Використовуючи формулу (6.1), для всіх елементів грошового потоку від 0 до n одержимо майбутнє значення грошового потоку

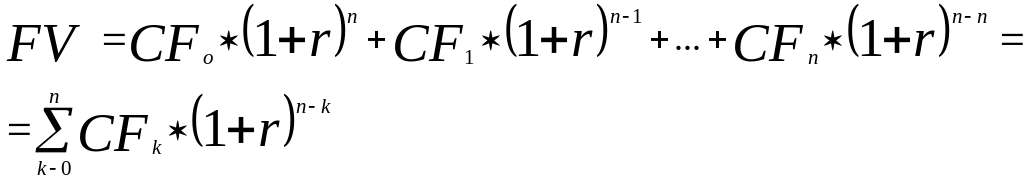, (5.5)

Приклад 5.4. Після впровадження заходу щодо зниження адміністративних витрат підприємство планує одержати економію $1,000 у рік. Зекономлені гроші передбачається розміщати на депозитний рахунок (під 5 % річних) для того, щоб через 5 років накопичені гроші використати для інвестування. Яка сума виявиться на банківському рахунку підприємства?

Вирішимо завдання з використанням тимчасової лінії.

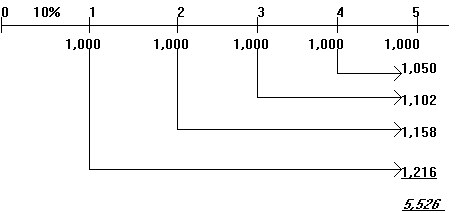
У такий спосіб через 5 років підприємство нагромадить $5,526, які зможе інвестувати.

У цьому випадку грошовий потік складається з однакових грошових сум щорічно. Такий потік називається ануїтетом. Для обчислення майбутнього значення ануїтету використається формула

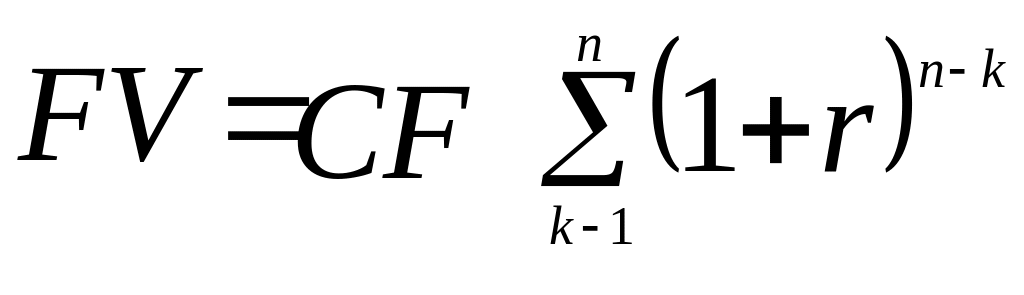, (5.6)

яка треба з (5.5) при CFk = const й CF0 = 0.

Розрахунок майбутнього значення ануїтету може провадитися за допомогою спеціальних фінансових таблиць.

Дисконтування грошових потоків здійснюється шляхом багаторазового використання формули (5.2), що в остаточному підсумку приводить до наступного вираження:

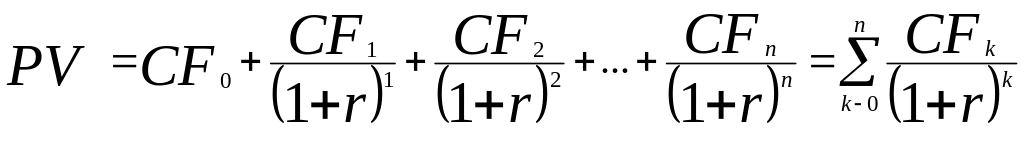, (5.7)

Приклад 5.5. Розглянемо грошовий потік з неоднаковими елементами CF1=100, CF2=200, CF3=200, CF4=200, CF5=200, CF6=0, CF7=1,000, для якого необхідно визначити сучасне значення (при показнику дисконту 6%). Рішення проводимо за допомогою тимчасової лінії:

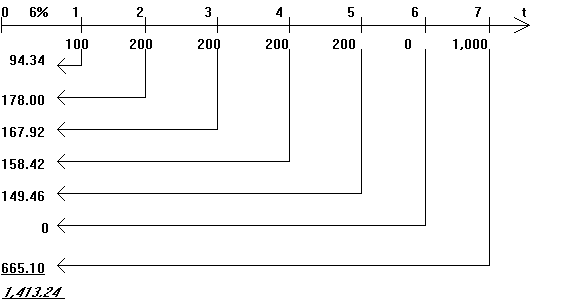
Обчислення дисконтированных значень окремих сум можна провадити шляхом використання таблиці 3, поміщеної в додатку

Дисконтування ануїтету (CFj = const) здійснюється по формулі

, (5.8)

Для розрахунку сьогодення (сучасного) значення аннуитета може бути використана таблиця 4 додатки.

Приклад 5.6. Підприємство придбало облігації муніципальної позики, які приносять йому доход $35,000, і хоче використати ці гроші для розвитку власного виробництва. Підприємство оцінює прибутковість інвестування одержуваних щороку $35,000 в 12 %. Необхідно визначити дійсне значення цього грошового потоку.

Рішення проведемо за допомогою таблиці:

Рік	Множник при 12% дисконтування	Потік грошей	Дійсне значення
1	0. 893	$35,000	$31,255
2	0. 797	$35,000	$27,895
3	0. 712	$35,000	$24,920
4	0. 636	$35,000	$22,260
5	0. 567	$35,000	$19,845
Сума	3. 605	$35,000	$126,175

За результатами розрахунків ми бачимо, що

дисконтоване значення грошового потоку істотно менше арифметичної суми елементів грошового потоку,

ніж далі ми заходимо в часі, тим менше дійсне значення грошей: $35,000 через рік коштують зараз $31,255; $35,000 через 5 років коштують зараз $19,845.

Завдання може бути вирішена також за допомогою таблиці 4 додатки. При r = 12% й n = 5 по таблиці знаходимо множник дисконтування 3.605.

Сучасне значення нескінченного (за часом) потоку коштів визначається по формулі:

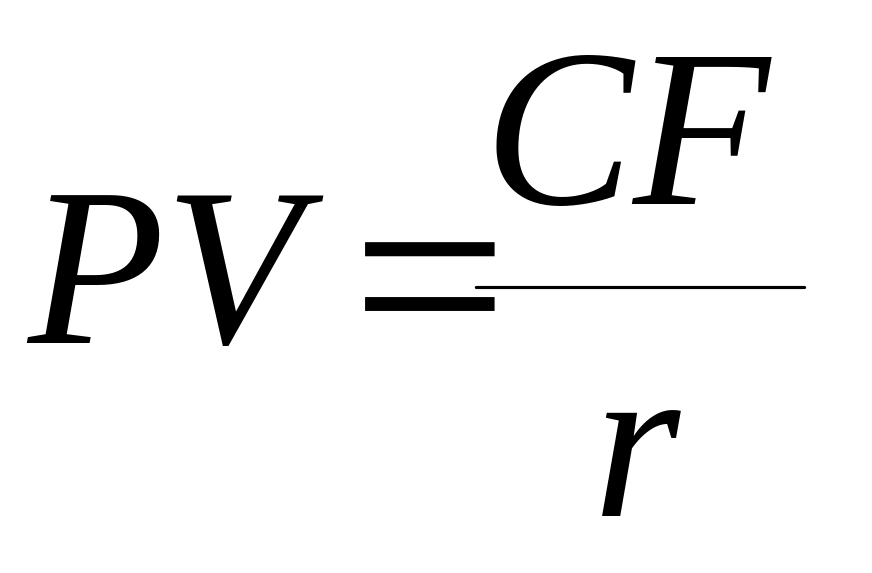, (5.9)

яка виходить шляхом підсумовування нескінченного ряду, обумовленого формулою (6.8) при .