Генеральная средняя

Определение. Генеральной средней называют среднее арифметическое значение признака генеральной совокупности:

,

где N - объем совокупности.

Выборочная средняя

Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема п.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности:

, или .

х_i – варианта выборки, п_i – частота варианты х_i, - объем выборки.

Рассмотрим некоторую совокупность, значений количественного признака Х объема п:

Значение признака	х1	х2	…	хк
Частота	п1	n2	…	пк

причем .

Отклонением называют разность между значением признака и общей средней.

Теорема. Сумма произведений отклонений на соответствующие частоты равна нулю

.

Генеральная дисперсия

Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику – генеральную дисперсию.

Смещенной оценкой генеральной дисперсии служит выборочная дисперсия:

.

Более удобна формула:

Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней

Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия:

.

Кроме дисперсии, для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой – средним квадратическим отклонением.

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выброчной дисперсии:

.

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:

.

Стандартное отклонение. Стандартное (среднеквадратичное) отклонение ( ) – это положительный квадратный корень из дисперсии. Оно вычисляется в тех же единицах (размерностях), что и исходные данные и характеризует степень рассеивания вариационного ряда вокруг средней. Чем меньше , тем более типична, точна средняя.

Оценка характеристик положения

Наиболее распространенными опенками характеристик положения являются среднее арифметическое выборки (выборочное среднее), выборочная медиана и выборочная мода. В дальнейшем будем, опускать термин «выборочная», имея, однако, в виду, что любая оценка, начисляемая по выборке, является всего лишь приближенным значением соответствующей характеристики генеральной совокупности

В качестве меры относительного разброса данных используют коэффициент вариации (процентное отношение среднеквадратического отклонения к среднеарифметической величине)

или

Коэффициент вариации — это относительная мера колеблемости вариационного ряда.

Применение коэффициента вариации

а) для оценки разнообразия каждого конкретного вариационного ряда и, соответственно, суждения о типичности отдельной средней (т.е. ее способности быть полноценной обобщающей характеристикой данного ряда). При С<10% разнообразие ряда считается слабым, при С от 10% до 20% - средним, а при С>20% - сильным. Сильное разнообразие ряда свидетельствует о малой представительности (типичности) соответствующей средней величины и, следовательно, о нецелесообразности ее использования в практических целях.

б) для сравнительной оценки разнообразия (колеблемости) разноименных вариационных рядов и выявления более-менее стабильных признаков, что имеет значение в дифференциальной диагностике.

ЗАДАЧА-ЭТАЛОН

Условие задачи. В городе N в 2000 г. проведено измерение массы тела 7-летних мальчиков. По данным аналогичного исследования, выполненного в городе N в 1990 г., средняя масса тела 7-летних мальчиков составила 23,8 кг, σ± 3,6 кг.

Задание. 1. Вычислить среднюю арифметическую величину ( ) и критерии разнообразия вариационного ряда (σ, С).

2. Оценить полученные результаты, сравнить их с данными предыдущего исследования, сделать соответствующие выводы.

РЕШЕНИЕ ЗАДАЧИ

Результаты измерения массы тела 7-летних мальчиков города N в 2000 г.

Масса тела (в кг)	Середина интервала (центральная варианта)	Число мальчиков
15-18,9	17	16	272	17-24=-7	49	49*16=784
19-22,9	21	27	567	21-24=-3	9	9*27=243
23-26,9	25	32	800	+1	1	32
27-30,9	29	16	464	+5	25	400
31-34,9	33	9	297	+9	81	729

В сгруппированном вариационном ряду центральная варианта рассчитывается как полусумма начальных вариант соседних интервалов.

Выводы:

1. Средняя масса тела 7-летних мальчиков в городе N в 2000 г. составляет 24,0 кг.

2. σ= ±4,68 кг.

3. Величина коэффициента вариации, равная 19,5%, свидетельствует о среднем разнообразии признака, приближающемся к сильному. Таким образом, можно считать, что полученная средняя величина массы тела является достаточно представительной (типичной) для изучаемой совокупности. По сравнению с 1990 г. в 2000-м отмечается более значительная вариабельность массы тела у мальчиков 7 лет (4,68 кг против 3,6 кг). Аналогичный вывод вытекает и из сопоставления коэффициентов вариации (C в 1990 г. равен (3,6*100)/23,8 =15,1%).

Стандартная ошибка среднего. Случайные ошибки выборок возникают за счет того, что для анализа всей совокупности используется только ее часть. Хотя выборочный метод и позволяет обоснованно судить о средней арифметической некоторого количественного признака генеральной совокупности по средней арифметической, исчисленной по выборке, это, однако, не означает, что выборочная средняя совпадает с генеральной средней. Она, как правило, в той или иной степени от нее отличается. Величина ошибки выборки представляет собой разность между генеральной и выборочной средними. Ошибки выборки различны для каждой конкретной выборки и в принципе могут быть обобщенно охарактеризованы с помощью средней из всех таких отдельных ошибок. В математической статистике получены формулы, которые позволяют приближенно вычислить среднюю ошибку выборки, основываясь на данных только той выборки, которая имеется в распоряжении исследователя.

Стандартная ошибка среднего отражает точность оценки среднего значения признака в популяции по его выборке. Небольшая стандартная ошибка (существенно меньше соответствующего среднего значения) означает достаточно точную оценку. Стандартная ошибка уменьшится, т. е. оценка станет более точной, если объем выборки увеличится или данные имеют небольшое рассеяние (дисперсию). При неограниченном увеличении объема выборки стандартная ошибка среднего обращается в 0. Следовательно, эта величина не имеет никакого биологического смысла.

Cтандартная ошибка среднего может быть найдена по формуле:

где – среднее квадратическое отклонение, – объем выборочной совокупности.

Доверительный интервал

Выборка из популяции позволяет получить точечную оценку интересующего нас параметра и вычислить стандартную ошибку для того, чтобы указать точность оценки. Следует отметить, что для большинства исследований стандартная ошибка как таковая неприемлема, поскольку она, в отличие от стандартного отклонения, не отражает вариабельности в значениях данных. Гораздо полезнее объединить эту меру точности с интервальной оценкой для параметра популяции. Для этого нужно вычислить доверительный интервал (ДИ), который дает вероятное значение верхней и нижней границ оцениваемой неизвестной величины, что позволяет заявить: «Я утверждаю, что точное значение неизвестной величины с определённой вероятностью (чаще всего эта вероятность составляет 0,95) находится между этими двумя числами».

Обычно доверительные интервалы показывают, насколько надежной в действительности является статистическая оценка. Например, утверждение, что в результате проведения лечебных мероприятий у группы больных среднее значение АД = 119,5 мм рт.ст. содержит некоторую определенную информацию. Однако утверждение, что врач на 95% уверен в том, что истинное (среднее популяционное) АД будет находиться в пределах от 115 до 125 мм рт.ст., позволяет сделать гораздо более глубокие выводы об эффективности лечения.

Доверительный интервал визуально удобно представлять в виде ящика с усами. Ящик с усами (англ. box-and-whiskers plot, box plot) – график, компактно изображающий одномерное распределение вероятностей. Несколько таких ящиков можно нарисовать бок о бок, чтобы визуально сравнивать одно распределение с другим.

В случае нормального распределения «ящик» рисуется на промежутке , где t– коэффициент Стьюдента – величина, зависящая от объема выборки (или соответствующего числа степеней свободы) и выбранного уровня доверительной вероятности, определяется по таблицам распределения Стьюдента; а m – стандартная ошибка среднего. Внутри «ящика» проводится риска – среднее арифметическое (рис. 1).

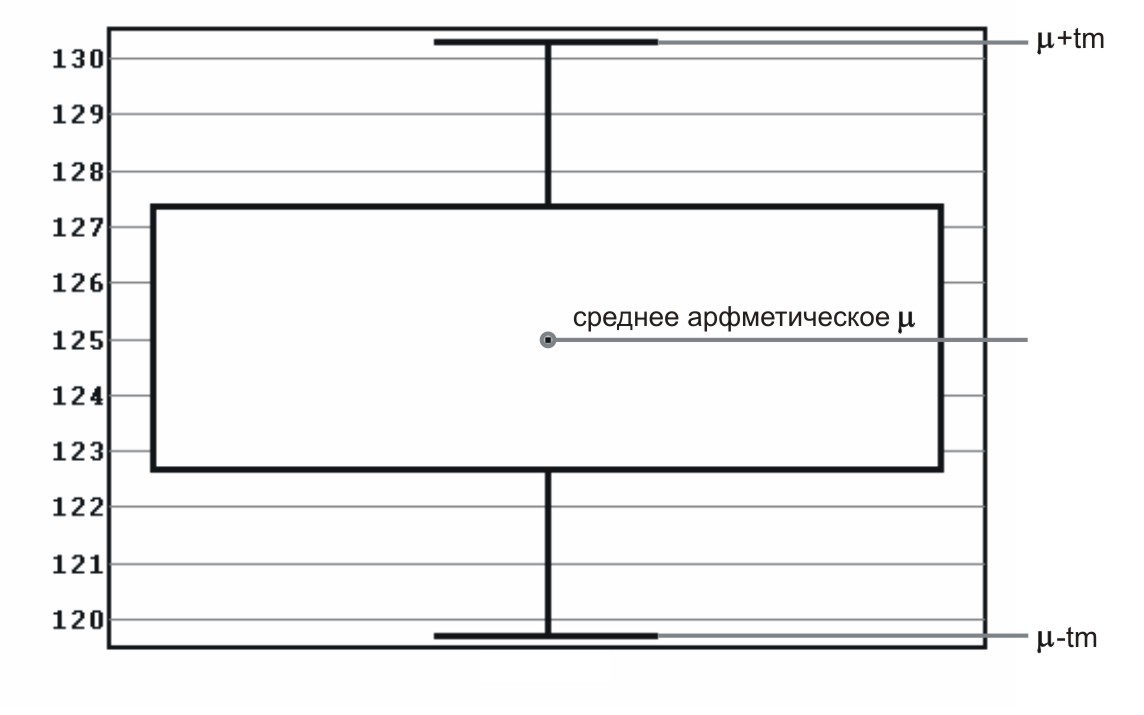
Рис. 1. Доверительный интервал для среднего в случае нормального распределения.

В случае распределения, отличного от нормального, вычисляют медиану x₅₀, квартили (x₂₅,x₇₅) и статистически значимый диапазон - например:

; .

«Ящик» рисуется от квартиля до квартиля, внутри него проводится риска – медиана. «Усы» тянутся от квартилей до статистически значимых крайних точек x₁ и x₂. Не входящие в статистически значимый диапазон точки (выбросы) изображаются отдельно (рис. 2).

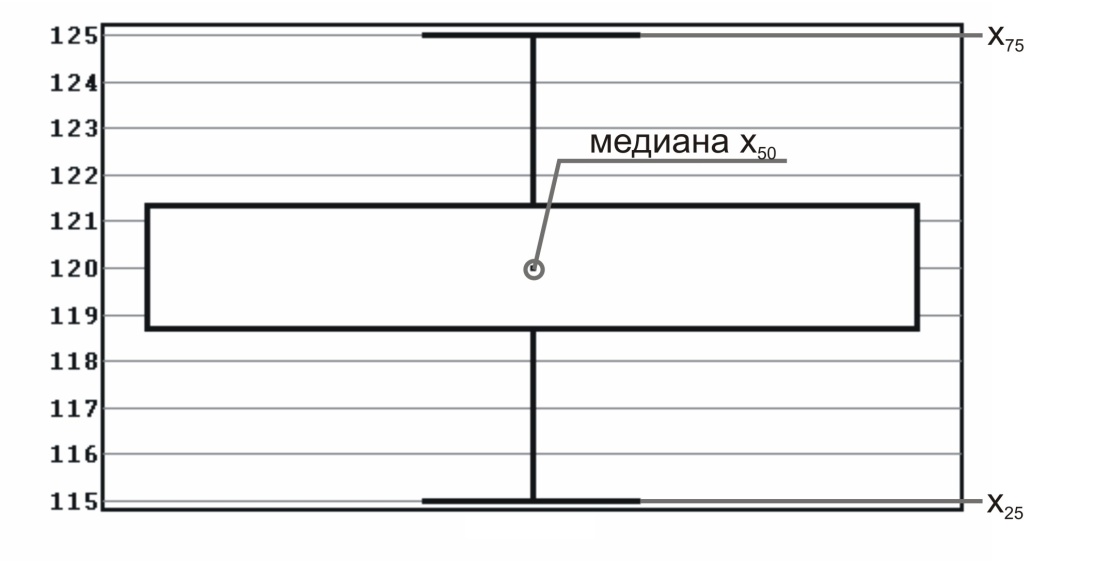
Рис. 2. Доверительный интервал для среднего (медианы) в случае распределения, отличного от нормального.

Доверительные интервалы представляют оценку в некоторой перспективе и позволяют избежать необходимости указывать одно и то же число как точное значение, в то время как фактически в биологии это число точным никогда и не является.

При интерпретации ДИ исследователь формулирует следующие вопросы: