7.4. Сложение колебаний Сложение двух колебаний одного направления

1. Частота и фазы одинаковы, амплитуды разные

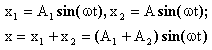(7.17)

- гармонические колебания той же частоты с суммарной амплитудой.

2. Частота и амплитуда одинаковы, фазы разные:

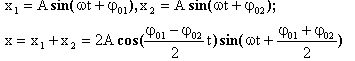(7.18)

- гармонические колебания той же частоты с амплитудой, зависящей от разности начальных фаз колебаний: при Δφ = 0 амплитуда максимальна, при

Δφ = π - колебания взаимно гасятся.

3. Амплитуды одинаковы, частоты разные

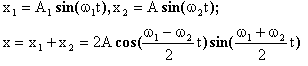(7.19)

негармонические колебания. Биения амплитуды с частотой ω₁ – ω₂ налагаются на (модулируют) несущую частоту колебаний (ω₁+ω₂)/2 (рис.7.6).

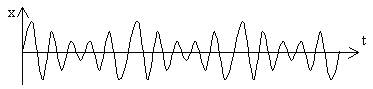
Рис. 7.6.

Найдем период колебаний в случае биений:

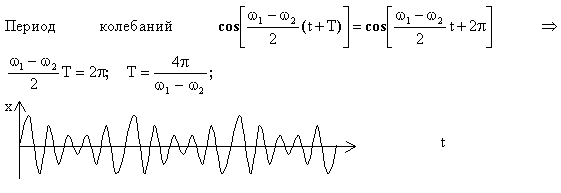
(7.20)

Сложение двух колебаний перпендикулярных направлений.

1. Частоты и фазы одинаковы, амплитуды разные

- гармонические колебания той же частоты с амплитудой .

2. Частоты одинаковы, фазы сдвинуты на 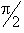, амплитуды различны:

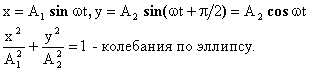
3. Частоты и амплитуды различны: 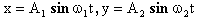- получаем либо незамкнутые траектории, либо фигуры Лиссажу (замкнутые кривые), если частоты кратные.

Фигуры Лиссажу

Фигуры Лиссажу - замкнутые траектории, прочерчиваемые точкой, совершающей гармонические колебания в двух взаимно перпендикулярных направлениях. Фигуры Лиссажу можно наблюдать с помощью осциллографа, подавая одновременно на вход X и вход Y (горизонтальные и вертикальные отклоняющие пластины) переменные напряжения кратных частот.

7.5. Свободные и вынужденные колебания.

Система, выведенная из состояния равновесия и предоставленная самой себе, совершает свободные колебания. Свободные колебания, совершаемые в среде без сопротивления, называются собственными колебаниями, частота которых определяется свойствами самой системы. Свободные колебания являются затухающими, потому что система расходует энергию на преодоление сопротивления среды, и амплитуда колебаний уменьшается - происходит диссипация энергии, т.к. . Для поддержания колебаний необходимо восполнить потери энергии извне, т.е. воздействовать на систему периодически изменяющейся силой

(7.21)

Вынужденными называются колебания системы под действием внешней периодической вынуждающей силы. На колеблющееся тело действуют три силы: вынуждающая, возвращающая и сила трения. Силу трения будем считать пропорциональной скорости v:

F_тр. = μv = μ(dx/dt). (7.22)

Вынужденные колебания происходят с частотой вынуждающей силы:

.

В таком случае уравнение движения имеет вид:

. (7.23)

Отсюда

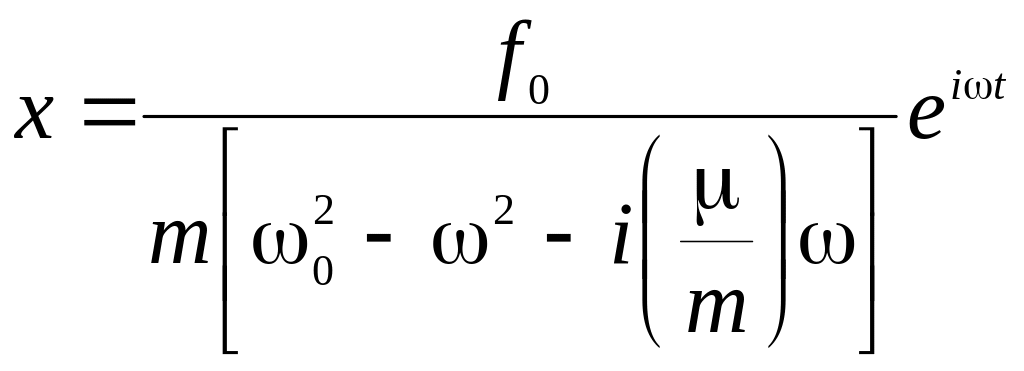. (7.24)

Если трение мало μ→ 0, то амплитуда вынужденных колебаний, равная . (7.25)

При совпадении частот собственного и вынужденного колебаний стремится к бесконечности.

Явление резкого возрастания амплитуды вынужденных колебаний при (рис. 7.7) называется резонансом.

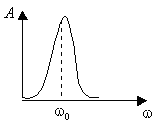
Рис. 7.7.

7.6. Затухающие колебания.

Уравнение затухающих колебаний представим в виде

(7.26)

Второе слагаемое - тормозящая сила (трение), пропорциональная скорости.

Решение уравнения имеет вид

, (7.27)

где .

Если β < ω₀, то амплитуда будет уменьшаться с течением времени по экспоненте (рис. 7.8).

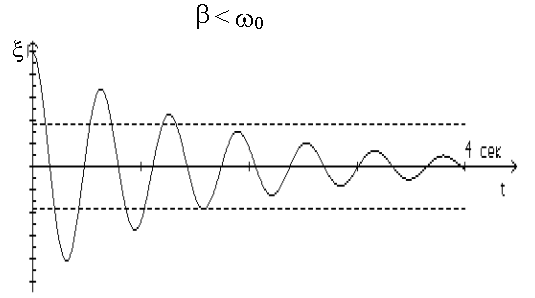
Рис. 7.8.

При β > ω₀ колебаний не возникает, процесс апериодический.