7. Колебательное движение.
7.1 Общие сведения о колебаниях.
Основной чертой колебательного движения является повторяемость с течением времени.
Колебаниями называются движения, повторяющиеся через равные или приблизительно равные промежутки времени. При периодических колебаниях повторяются траектория, скорость и ускорение материальной точки в любой точке траектории (рис. 7.1).
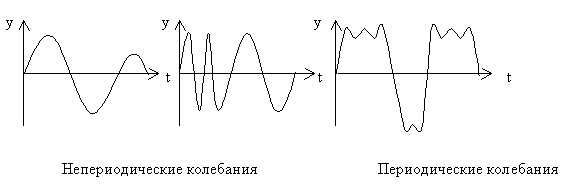
Рис. 7.1.
Параметры механических колебаний:
Амплитуда - наибольшее отклонение системы от положения равновесия;
Период - время между двумя последовательными прохождениями системы через одно и то же положение в одном и том же направлении;
Частота - число колебаний системы за единицу времени.
7.2. Гармонические колебания
Движение материальной точки по окружности можно трактовать как колебания проекций на оси X и Y около центра окружности.
Если т. М в начальный момент не совпадает с осью x, то необходимо добавить начальный угол φ0, т.о. уравнения гармонических колебаний (законы движения точек) имеют вид:
(7.1)
Величина ωt + φ0 называется фазой колебания, ω-круговой частотой, φ0 –начальной фазой. Скорость и ускорение колеблющейся точки являются также периодическими функциями времени:
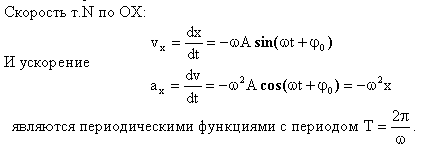
Дифференциальное уравнение гармонических колебаний
Рассмотрим колебания груза, прикрепленного к пружине (пружинный маятник). X – координата груза (рис. 7.2).
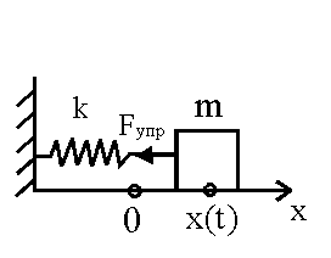
Рис. 7.2.
Второй
закон Ньютона
.
После проецирования на ось x:
,
.
Ax
= d2x/dt2,
получим
(7.2)
Используя другое обозначение производной получим после несложных преобразований:
(7.3)
Мы получили дифференциальные уравнения, описывающие движение груза.
Введем
обозначения:
;
x = ξ, подставим в предыдущее равенство,
получим дифференциальное уравнение
гармонических колебаний любой природы:
(7.4)
При гармонических колебаниях происходит взаимное периодическое превращение кинетической и потенциальной энергии.
Но k = mω2. Таким образом, полная механическая энергия равна:
(7.5)
Механическая энергия постоянна и пропорциональна квадрату амплитуды и квадрату частоты.
Решение дифференциального уравнения
Решением
дифференциального уравнения называется
функция,
обращающая это уравнение в тождество.
Нетрудно проверить прямой подстановкой,
что в нашем случае решение
имеет вид:
,
т.е. является гармонической функцией.
Значит уравнение
,
это дифференциальное уравнение
гармонических колебаний.
В случае гармонических колебаний зависимость координаты колеблющейся системы от времени часто оказывается удобным представлять в виде вещественной части комплексного выражения, представленного в экспоненциальной форме:
(7.6)
где число e – основание натуральных логарифмов; A — комплексная постоянная величина. Записав ее в виде
A = aeiα, (7.7)
мы вернемся к старому выражению
x = Re aeiω t+iα = a cos(ω t+α ). (7.8)
Постоянную величину A называют комплексной амплитудой. Ее модуль совпадает с обычной амплитудой, а аргумент — с начальной фазой колебаний.
Оперирование экспоненциальными множителями проще в математическом отношении, чем тригонометрическими, так как дифференцирование не изменяет их вида. При этом пока мы производим лишь линейные операции (сложение, умножение на постоянные множители, дифференцирование, интегрирование), можно вообще опускать знак вещественной части, переходя к последней лишь в окончательном результате вычислений.