Методика вивчення тотожних перетворень в основній школі

План

1. Місце в програмі. Вимоги до знань умінь............................................................

2. Формування провідних понять теми.....................................................................

3. Вивчення тотожних перетворень цілих виразів..................................................

4. Типові помилки учнів і шляхи їх подолання................................. .

1. Місце в програмі. Вимоги до знань та вмінь.

У програмі з алгебри для 7 класу передбачено 33 години для вивчення виразів та їх перетворень. За цей час учні повинні повторити й уточнити відомості про числові та буквені вираз, формули. Поряд з цим вводяться поняття:

• цілого раціонального виразу;

• степеня з натуральним показником;

• одночлена і многочлена;

• тотожно рівних виразів;

• тотожності, тотожні перетворення виразів;

• формули скороченого множення і застосування їх до перетворення многочленів.

У результаті вивчення теми “Цілі вирази” учні повинні

знати:

уміти:

У 8 класі передбачено вивчення тотожних перетворень раціональних дробів, дробових виразів і перетворень ірраціональних виразів, пов’язаних з квадратним коренем.

За чинною програмою у 8 класі вводять поняття:

• степеня з цілим показником і розглядаються перетворення найпростіших виразів, що містять степені з від’ємним показником;

• квадратного кореня, арифметичного квадратного кореня та його властивості.

Вимоги до математичної підготовки учнів 8 класу з вище згаданих питань можна сформулювати так:

Мати уявлення про:

- степінь з нульовим показником, цілим від’ємним показником, його властивості;

• стандартний вигляд числа;

• алгебраїчний дріб, раціональний і дробовий вираз;

• раціональні рівняння;

• квадратний корінь, арифметичний квадратний корінь;

• ірраціональні та дійсні числа.

Знати:

Уміти:

У 9 класі тотожні перетворення цілих і дробових виразів використовуються для розв’язування рівнянь, нерівностей, систем рівнянь. Вводиться нове перетворення – розкладання квадратного тричлена на множники, яке використовується для побудови графіка квадратичної функції.

2. Формування основних понять теми

До основних понять теми належать: “числовий вираз”, “вираз із змінними” або “буквений вираз”, “тотожно рівні вирази”, ”одночлени”, “многочлени”, ”перетворення виразу”, “тотожне перетворення”, “дроби”, “дробовий вираз”, “раціональні вирази”.

Поняття виразу. Перетворення виразів.

З поняттями “вирази”, “значення виразу” та відповідними термінами учні ознайомлюються ще у молодших класах. У І-ІІ класах вводиться поняття суми, різниці, добутку і частки двох чисел. У ІІІ - IV класі розглядають числові вирази. Спрощення числових виразів виконують у V, використовуючи відомі учням закони арифметичних дій. Пропедевтично у V-VI класах розглядаються коефіцієнт і зведення подібних доданків. Ці спрощення потрібні для розв’язування рівняння. У VI класі вводять поняття ”взяття в дужки”, “винесення многочлена за дужки”, “зведення подібних доданків”. Спрощення виразів проводилося без введення відповідних термінів.

Систематичне вивчення виразів та їх перетворення починається у 7 класі.

Методисти не рекомендують давати означення поняття “вираз”, оскільки його важко сформулювати для учнів цього віку. Поняття про вирази (числові та буквені) формуються описово на конкретних прикладах. Окремі види виразів вводяться поступово, із вивченням програмового матеріалу.

Поняття тотожності, тотожно рівних виразів на рівні означень вводяться вперше у 7 класі. Поняття тотожних перетворень виразів пояснюється описово на прикладах. Досвідчені вчителі не рекомендують давати формальне означення тотожно рівних виразів, тотожних перетворень виразів. Краще ці поняття вводити на одному уроці, пов’язавши їх з потребою обчислення виразу, тобто конкретно-індуктивним методом.

На дошці записується вираз

9·а+5·(b-a)+18·b+6·a-3·b= (1)

9·а+5·b-5a+18·b+6·a-3·b= (2)

(9а-5a+6a) +(5b+18b-3b)=10a+20b (3)

Перехід до нового виразу обґрунтується законами дій

Вчитель пропонує обчислити значення виразу (3) при а=6,25, b=12.5, що дорівнює 315,5, тоді. звертається увага, що при а=6,25, b=12.5 значення виразів (1) і (2) також дорівнює 315,5, але обчислювати їх доведеться значно довше

Вирази (1)-(3) називають тотожно рівними. Після цього формується означення тотожно рівних виразів.

Аналізуючи знову вирази (1)-(3), вчитель вводить поняття тотожного перетворення виразу. Підкреслюється той факт, що раніше, спрощуючи вирази на основі законів арифметичних дій, учні фактично виконували їх тотожні перетворення.

Означення поняття тотожності у 7 класі вводиться на множині цілих виразів, а у 8 класі розширюється і дається нове означення тотожності, як рівності правильної лише за всіх допустимих значень змінних, що входять до її складу.

Для учнів 8 класу складнішими для сприймання є поняття “цілий вираз” бо він асоціюється з відомим їм поняттям цілого числа, а “дробовий вираз” — з поняттям звичайного дробу як числа

У 8 класі слід уточнити, узагальнити і розширити уявлення учнів про вирази:

- раціональним називають вирази, які утворені з чисел із змінних за допомогою додавання, віднімання, множення, ділення.

10х²у; 53; ;

Раціональні вирази можна поділити на два класи: цілі і дробові вирази. Цілими називаються вирази, складені з чисел і змінних за допомогою дій додавання, віднімання, множення і ділення на число, відмінне від нуля.

Дробовими раціональними виразами називаються раціональні вирази, які містять ділення на змінну або вираз із змінною.

У 8 класі учні вперше стикаються з ірраціональними виразами. На цьому етапі навчання вони мають справу лише з ірраціональними виразами, які містять арифметичні квадратні корені.

Поняття одночлена.

Дидактична мета вивчення пункту: ввести поняття одночлена; продовжити формування навичок дій зі степенями.

Основні знання: уміти відрізняти одночлен від виразу, який не є одночленом; уміти перетворювати одночлен в одночлен стандартного вигляду.

Методичні рекомендації.

Поняття одночлена доцільно формувати конкретно-індуктивним методом, розглядаючи приклади: 5; х; -а; 5ab; 2,5x⁵; a²+b². Формального означення поняття одночлена не дається.

Одним з найважливіших представників класу тотожних перетворень у 7 класі є зведення одночленів до стандартного вигляду. Мотивується це перетворення потребою спрощення одночлена, одержаного при множені одночленів.

При зведенні одночлена до стандартного вигляду важливим є поняття коефіцієнта. Учні неправильно визначають коефіцієнти біля змінної у випадках, коли вони дорівнюють 1 та -1. За домовленістю їх не пишуть, а число -1 замінюють знаком мінус.

Важливо підкреслити теоретичну основу виконання перетворення: під час зведення одночлена до стандартного вигляду використовується переставний, сполучний закон множення і правило множення степенів з однаковою основою.

Після розгляду кількох прикладів формується правило: Щоб привести одночлени до стандартного вигляду, треба перемножити числові множники і степені змінних з однією основою.

Слід ввести вимогу:

1. У запису одночлена стандартного вигляду дужки не ставляться.

2. Одночлен має тільки один числовий множник, який записується на першому місці.

3. Кожний добуток однакових змінних подається у відповідному степені. Наприклад 3хххуух=3х⁴у²

Важливо зауважити, щоб будь-яке число є одночленом записаним у стандартному вигляді.

Основне призначення вправ на цьому уроці полягає у виробленні вміння зводити вирази до стандартного виду одночлена.

На закріплення пропонуються вправи типу:

1. Назвіть коефіцієнти одночленів:

6a³b²; -3а²b³; 7; a⁷b2; -a²b²; -5.

2. Які з одночленів 3a²b³; (-7)a²b³; 3(a²b³); (-1)a³b³; a²b²; 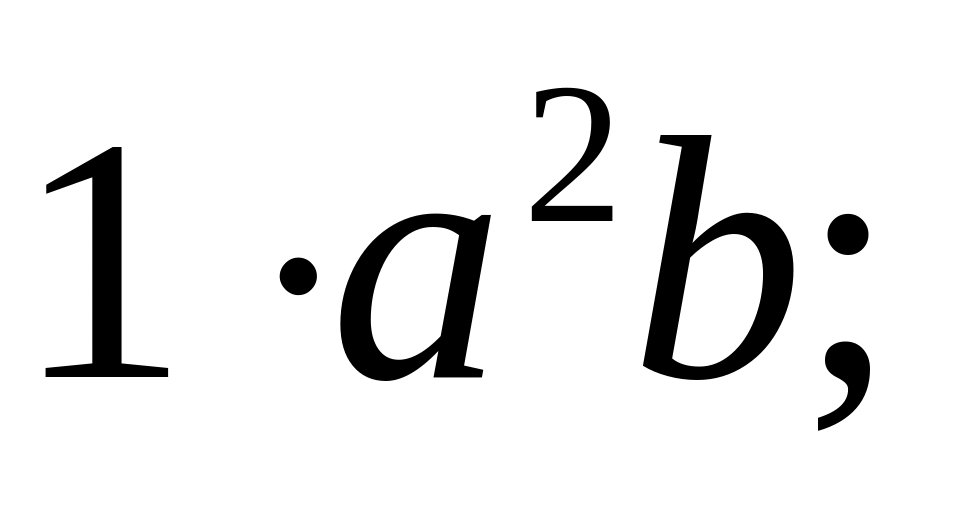-a²b³ мають стандартний вигляд?

3. Зведіть до стандартного вигляду одночлени.

4. Подайте дані одночлени у вигляді добутку двох одночленів, з яких один заданого вигляду:

Наприклад, запишіть одночлен -54х³у²у у вигляді добутку двох одночленів, з яких один -9х²у.

Піднесення одночленів до степеня не викликає труднощів у школярів. Проте деякі з них забувають підносити до степеня коефіцієнт.

Многочлени

Дидактична мета вивчення пункту: ввести поняття многочлена; навчити зводити многочлени, додавати і віднімати многочлени; множити многочлен на одночлен та на інші многочлени.

Методичні рекомендації.

Поняття многочлени не викликає в учнів труднощів. Основне що повинні опанувати семикласники під час вивчення теми “Многочлени” – це навчитися додавати, віднімати і множити многочлени.

Поняття многочлена зручно формувати розглядаючи суму двох і більше одночленів. При цьому корисно розглянути випадок коли коефіцієнт хоч би одного одночлена є від’ємним.

За програмою вивчається дія множення многочлена на одночлени і многочлена на многочлен.