16

В случае контрольной работы, студент выполняет 2 лабораторные работы, согласно начальной буквы его фамилии из данной методички

Начальная буква фамилии студента	№ лабораторной работы	Начальная буква фамилии студента	№ лабораторной работы
А, К, У	1, 5	Е, П, Ш	1, 3
Б, Л, Ф	2, 7	Ж, Р, Щ	4, 2
В, М, Х	3, 6	З, С, Э	5, 2
Г, Н, Ц	4, 6	И, Т, Ю, Я	6, 7
Д, О, Ч	5, 4

При формировании системы показателей изменения уровней ряда динамики принято сравниваемый уровень называть отчетным, а уровень, с которым производят сравнение – базисным [7].

Абсолютный прирост (у) – характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Физически он означает абсолютную скорость роста процесса (явления)

; (1)

где i = 1, 2, 3, ..,n.

Если k=1 то уровень y_{i – 1} является предыдущим для данного ряда, а абсолютные приросты изменения будут цепными. Если k постоянно для данного ряда, то абсолютные приросты будут базисными.

Коэффициент роста или темп роста представляет собой две формы выражения интенсивности изменения уровня.

Коэффициент роста показывает во сколько раз данный уровень ряда больше (меньше) базисного уровня за некоторый промежуток времени.

В качестве базисного уровня в зависимости от цели исследования может приниматься какой-то постоянный для всех уровень (часто начальный уровень ряда) либо для каждого последующего, предшествующий ему.

(2)

В первом случае говорят о базисных темпах роста, во втором – о цепных темпах роста.

Наряду с темпом роста существует показатель темпа прироста, характеризующий относительную скорость изменения уровня ряда в единицу времени. Физически темп прироста показывает, на какую долю (или процент) уровень данного периода или момента времени больше (или меньше) базисного уровня. Он представляет собой отношение абсолютного прироста к уровню ряда, принятого за базу

(3)

Если темп роста всегда положительно число, то темп прироста может быть положительным, отрицательным или равным нулю.

В статистической практике часто вместо расчета и анализа темпов роста и прироста рассматривается абсолютное значение одного процента прироста, представляющего собой одну сотую часть базисного уровня и в то же время отношение абсолютного прироста к соответствующему темпу прироста

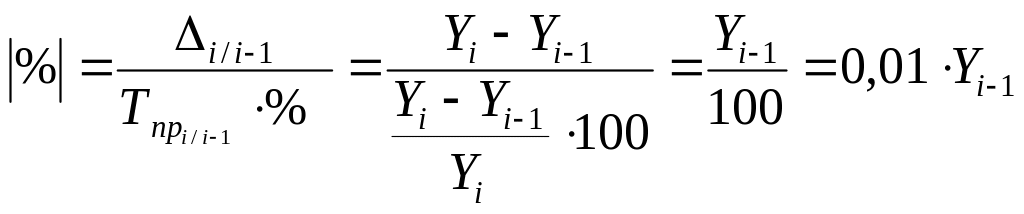, (4)

где% – обозначение абсолютного значения 1% прироста.

Абсолютное значение одного процента прироста служит косвенной мерой базисного уровня и вместе с темпом прироста позволяет рассчитать абсолютный прирост уровня за рассматриваемый период.

Ускорением в статистике называется разность между последующим и предыдущим абсолютными приростами

. (5)

Ускорение показывает, насколько данная скорость больше (меньше) предыдущей.

Относительным ускорением называется отношение абсолютного ускорения к абсолютному приросту, принятому за базу , т.е. относительное ускорение есть темп прироста абсолютного прироста. Оно вычисляется лишь в том случае, если абсолютный прирост, принятый за базу сравнения, число положительное.

Средний уровень ряда динамики ( ) рассчитывается по зависимости, используемой для средней хронологической.

Средней хронологической называется средняя, исчисленная из значений, изменяющихся во времени.

Методы расчета среднего уровня интервального и моментного рядов динамики различны.

Для интервальных рядов с равноотстоящими уровнями средний уровень находится по формуле средней арифметической простой, а для не равноотстоящих уровней – по средней арифметической средней взвешенной

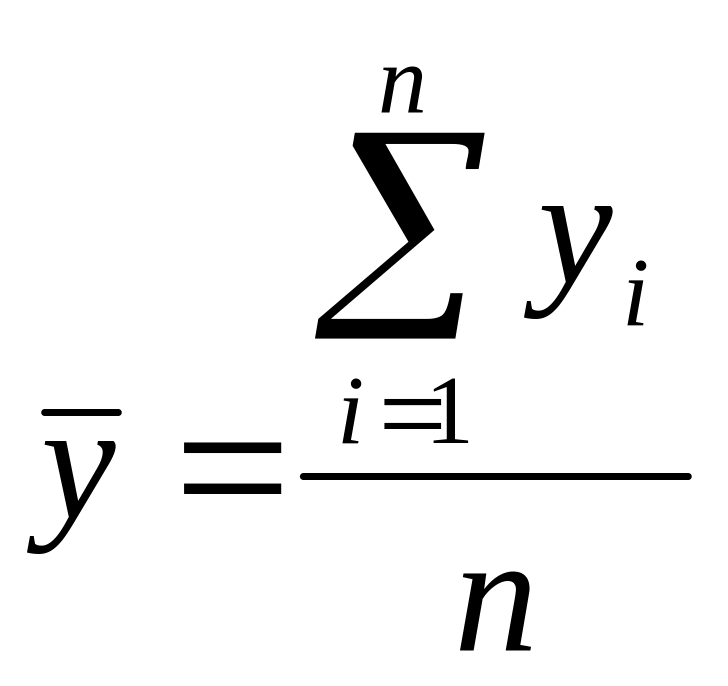; (6)

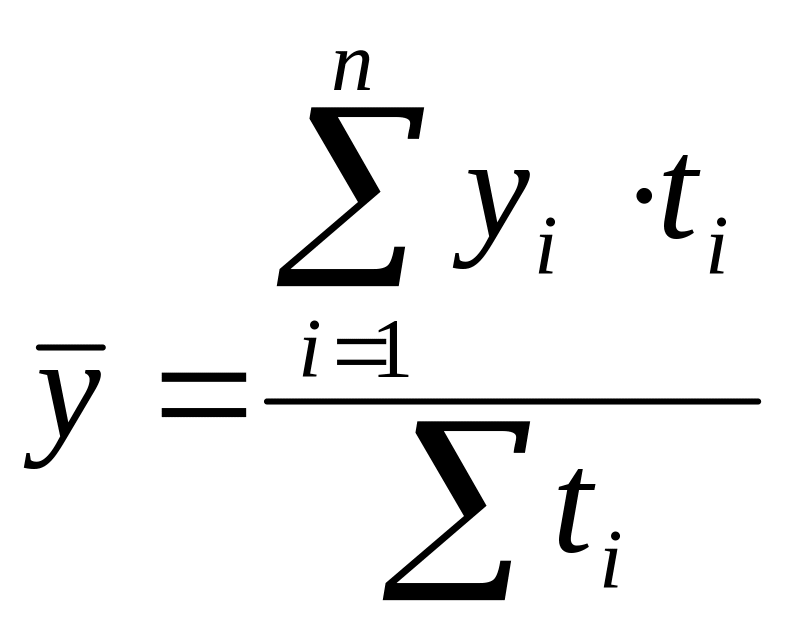, (7)

где y_i - уровень ряда динамики;

n - число уровней;

t_i - длительность интервала времени между уровнями.

Средний уровень моментного ряда динамики по приведенным выше зависимостям рассчитывать не представляется возможным, так как отдельные уровни ряда, как правило, будут содержать элементы повторного счета.

Средний уровень моментного равноотстоящего ряда динамики находится по формуле

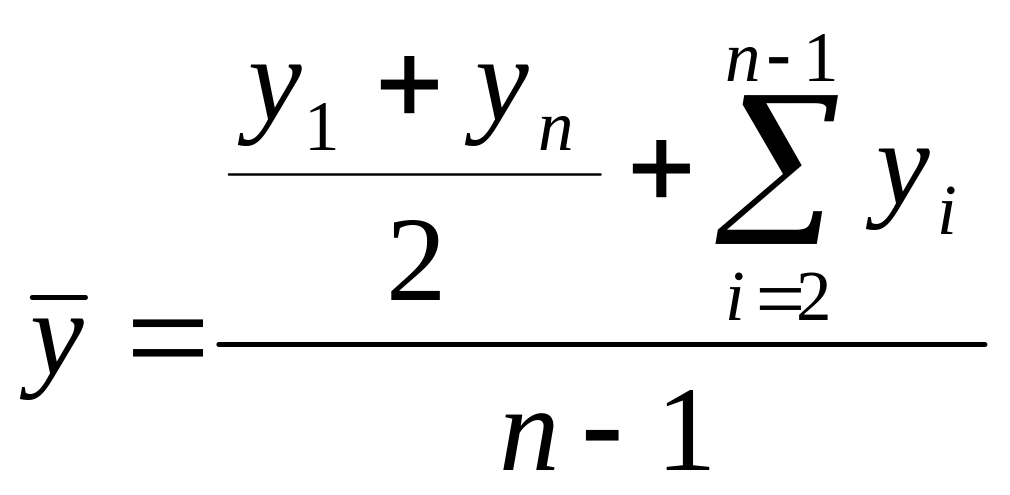. (8)

Средний уровень моментных рядов динамики с неравноотстоящими уровнями определяется по формуле средней хронологической взвешенной

, (9)

где y₁ , y_n - уровни рядов динамики;

t_i - длительность интервала времени между уровнями.

Средний абсолютный прирост ( ) – является обобщающим показателем скорости изменения явления во времени. Физически этот показатель означает возможность оценки насколько в среднем за единицу времени должен увеличиваться уровень ряда (в абсолютном выражении), чтобы, отправляясь от начального уровня за данное число периодов (например, лет) достигнуть конечного уровня. Для его определения используется зависимость для средней арифметической простой

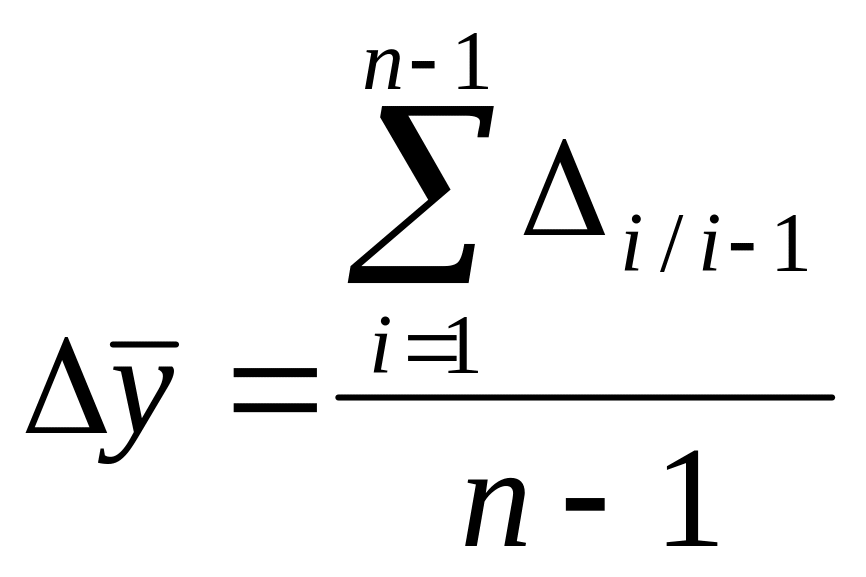(10)

или

(11)

Возможен и другой способ расчета среднего абсолютного прироста, исходя из куммулятивных данных

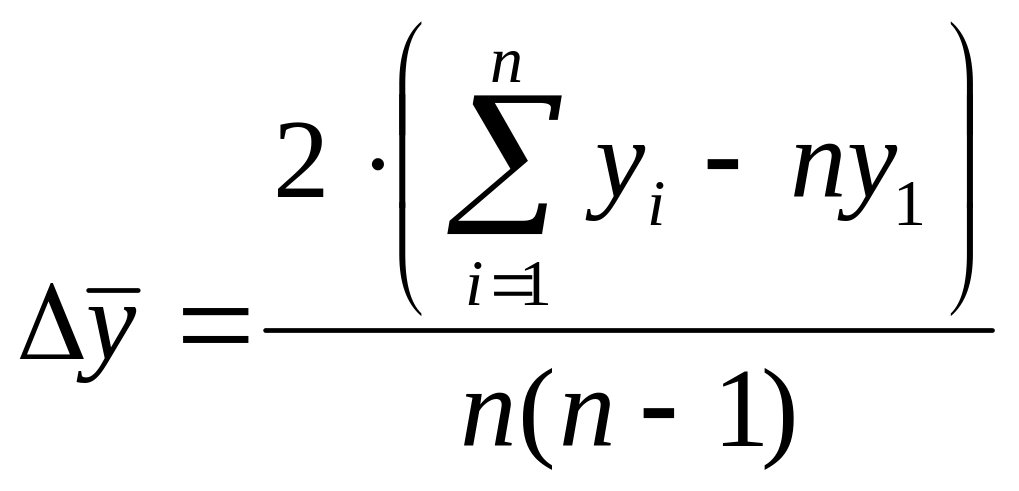. (12)

Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит темп роста, показывающий, во сколько раз в среднем за единицу времени изменился уровень динамического ряда.

Обычно средний темп роста вычисляется по формуле средней геометрической из цепных коэффициентов роста

где К_Рi/i-1 -цепные коэффициенты роста (отношение Y_i / Y_i-1)

Существует более простая зависимость для определения среднего темпа роста, которая имеет вид

. (13)

При расчете средних темпов роста по периодам различной продолжительности (разно отстоящие ряды динамики) пользуются средними геометрическими взвешенными по продолжительности периодов. Формула средней геометрической взвешенной будет иметь вид

, (14)

где t - интервал времени, в течении которого сохраняется данный темп роста.

t - сумма отрезков времени периода.

Имея основные зависимости для оценки показателей уровня ряда динамики можно приступить к простейшим видам прогнозирования основанным на анализе абсолютного прироста уровня ряда и его среднего темпа роста.

Прогнозирование по среднему абсолютному приросту применяется в том случае, когда есть уверенность считать абсолютную тенденцию линейной т.е. метод основан на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов). В данном случае экстраполяция осуществляется по зависимости

, (15)

где – экстраполируемый уровень: (i+t) – номер этого уровня (года);

i – номер последнего уровня (года) исследуемого периода, за который рассчитан ;

t – срок прогноза ( период упреждения);

– средний абсолютный прирост.

Следует иметь ввиду! Использование среднего абсолютного прироста для прогноза возможно только при выполнении следующего условия

, (16)

где ; .

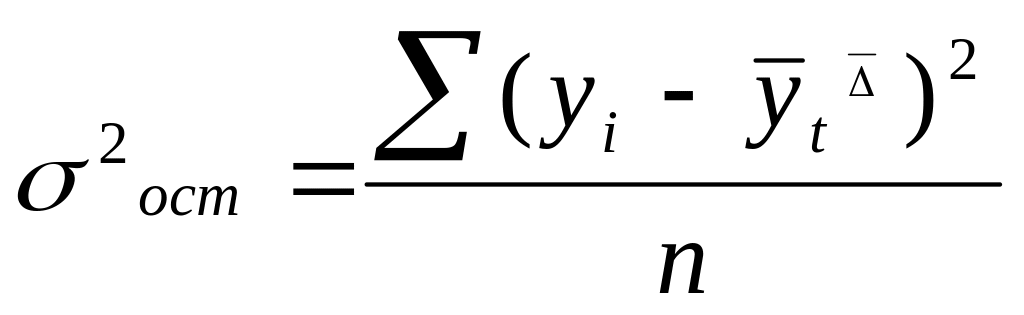Выполним прогнозирование прожиточного минимума населения Пензенской области в первом квартале 1998 года, используя поквартальные статистические данные о прожиточном минимуме в 1997 году. Исходные данные, заимствованные из сборника «Социально–экономическое положение Пензенской области в январе 1999г. с. 88» приведены в таблице 1.

Таблица 1. Прожиточный минимум населения Пензенской области в 1997г.

Год (квартал)	Прожиточный минимум, рубл..уi	i	(i )2		(уi - )2
1-квартал 2 - квартал 3 – квартал 4 – квартал	362,6 374,5 366,2 371,0	- 11,9 -8,3 4,8	- 141,6 68,9 23,0	362,6 365,4 368,2 371,0	0 82,8 4,0 0
Итого	1474,3	-	233,5	-	86,8

Средний абсолютный прирост ряда равняется

.

.

.

Так, как условие (16) выполняется, то данный метод применим для использования прогноза. Тогда прожиточный минимум населения Пензенской области в первом квартале 1998 года следует ожидать

= 371,0 + 2,8 = 373,8 руб.

Сравнивая результаты прогноза с данными Пензенского Госкомоблстата получим ошибку прогноза

 = 387,4 – 373,8 = 13,6 руб.

Выполним аналогичные вычисления прогноза прожиточного минимума в первом квартале 1999 используя данные прожиточного минимума в 1998 году (таблица 2).

Таблица 2. Прожиточный минимум населения Пензенской области в 1998г.

Год (квартал)	Прожиточный минимум, руб. уi	i	(i )2		(уi - )2
1-квартал 2 - квартал 3 – квартал 4 – квартал	387,4 387,3 418,7 560,4	- -0,1 31,4 141,7	- 0,01 986,0 20078,9	387,4 445,0 502,6 560,2	0 3329,3 7039,2 0
Итого	1753,8	-	21064,9	-	10368,5

.

Так, как условие (16) выполняется, то данный метод применим для использования прогноза. Тогда прожиточный минимум населения Пензенской области в первом квартале 1999 года следует ожидать

= 560,4 + 57,6 = 618 руб.

Сравнивая результаты прогноза с данными, приведенными в Информационном Бюллетене Министерства труда и социального развития правительства Пензенской области № 13, 2000г., получим ошибку прогноза

 = 730 – 618 = 112 руб.

Анализируя данные двух прогнозов можно сделать вывод, что для первого прогноза получены удовлетворительные результаты и, наоборот, для второго случая данные прогноза получились явно заниженными. Поэтому произведем вычисления, пользуясь вторым методом прогноза.

Прогнозирование по среднему темпу роста осуществляется в случае, когда установлено, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения тенденции необходимо определить средний коэффициент роста, возведенный в степень, соответствующую периоду экстраполяции

, (17)

где y_i – последний уровень ряда динамики;

t – срок прогноза;

- средний коэффициент роста.

Тогда для данных табл. 2 имеем

У_{4-квр. 98г.} = 560,4; .

Прогнозируемая величина прожиточного минимума в первом квартале 1999 года в соответствии с зависимостью (17) равна

У_{1-квр. 99г.} = 560,4* 1,13 = 633,2 руб.

Ошибка прогноза (=730–633,2=96,8 руб.) несколько уменьшилась, но все равно является значительной.

Рассмотренные выше способы экстраполяции являются весьма приближенными. Потому наиболее распространенным методом прогнозирования является метод аналитического выражения тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значение независимой переменной времени (t).

Проверка наличия тенденции (тренда).

Существует около десятка критериев проверки наличия тренда, наиболее распространенными их них является критерий, связанный с проверкой существенности разности средних и критерий определяемый по методу Фостера–Стюарта [7].

При проверке существенности разности средних ряд динамики разбивается на две равные или почти равные части. Проверяется гипотеза о существовании разности средних:

Н₀: _.

Так как число членов анализируемого ряда, как правило, мало, то для проверки гипотезы воспользуемся теорий малой выборки. За основу проверки берется t – критерий Стьюдента. При t  t гипотеза об отсутствии тренда отвергается и наоборот при t  или  t гипотеза (Н₀) принимается. Здесь t – расчетное значение, найденное для анализируемых данных. t – табличное значение критерия при уровне вероятности ошибки, равном .

В случае равенства или при несущественном различии дисперсий двух исследуемых совокупностей ( = ) определение расчетного значения t производится по зависимости

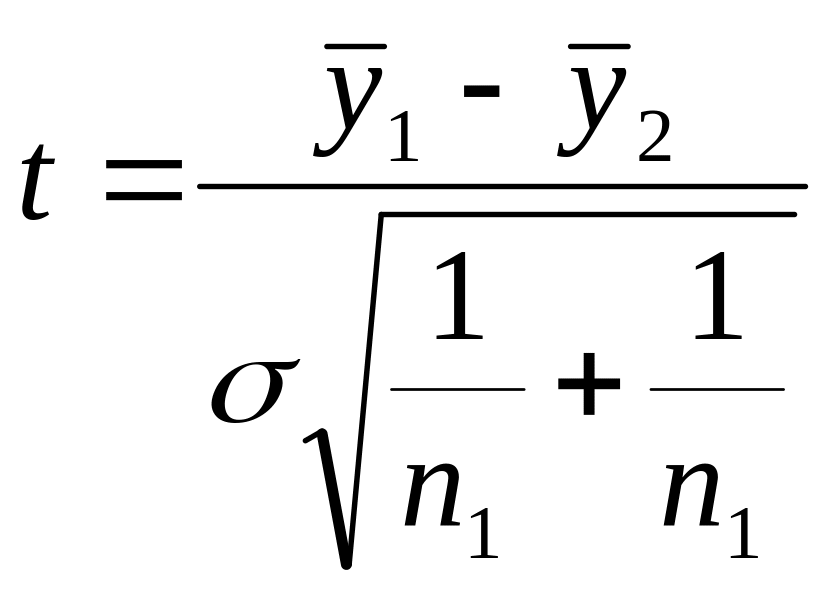, (18)

где и средние для первой и второй половины ряда динамики;

n₁ и n₂ - число наблюдений в этих рядах;

 – среднеквадратическое отклонение разности средних., определяемое по зависимости

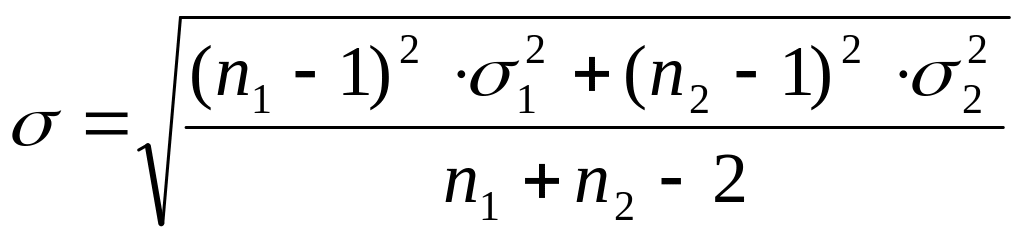. (19)

Дисперсии для первой и второй частей ряда рассчитываются по зависимости

(20).

Проверка гипотезы о равенстве дисперсией осуществляется с помощью F-критерия, основанного на сравнении расчетного отношения с табличным. Расчетное значение критерия определяется по формуле

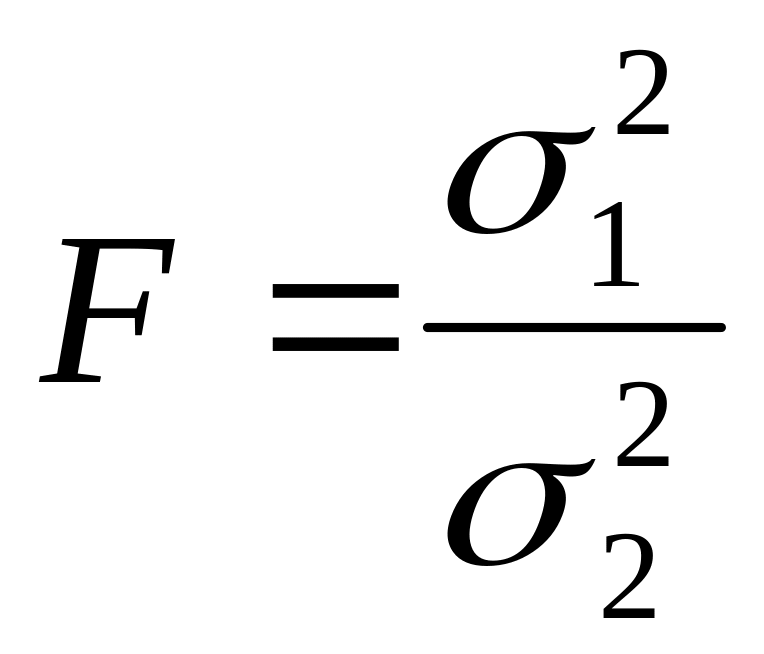, (21)

Если расчетное значение F меньше табличного, при заданном уровне вероятности, то гипотеза о равенстве дисперсией принимается. Если F больше, чем табличное значение, то гипотеза о равенстве дисперсий отклоняется и зависимость для расчета t не пригодна для использования.

При выполнении условия о равенстве дисперсий, определяется значение t и проверяется гипотеза (Н₀). При этом теоретическое значение t определяется с числом степеней свободы равным n₁ +n₂–2

В заключении следует отметить, что изложенный выше метод дает положительные результаты для рядов с монотонной тенденцией. Когда же ряд динамики меняет общее направление развития, то точка поворота тенденции оказывается близкой к середине ряда. Поэтому средние двух отрезков будут близки, а проверка может не показать наличие тенденции.

Метод Фостера–Стюарта помимо определения наличия тенденции позволяет также обнаружить тренд дисперсии уровней ряда динамики, что важно знать при анализе и прогнозировании социально - экономических явлений.

Алгоритм расчета состоит из следующих этапов.

1. Производится сравнение каждого уровня ряда со всеми предыдущими, при этом

Если у_i > у_i-1; у_i-2 …, у₁, то U_i = 1 ; e_i = 0;

При у_{i <} у_i-1; у_i-2 …, у₁, то U_i = 0 ; e_i = 1;

2. Вычисляются значения величин S и d

S = ∑S_i ; d = ∑d_i , (22)

где S_i = U_i + e_i ;

d_i = U_i - e_i.

Анализируя формулу (22) нетрудно заметить, что величина S может принимать значения в интервале 0 < или = S < или = n –1, причем S=0, когда все уровни равны между собой, и S = n – 1, когда ряд динамики монотонно убывает или возрастает. Показатель S характеризует тенденцию изменения дисперсий ряда динамики.

Если все уровни ряда равны между собой, тогда ∑U_i =∑e_i (данное условие выполняется для ряда, который в первой половине является монотонно убывающим, а во второй – монотонно возрастающим).

Если уровни подъема и спада чередуются, причем каждое следующее значение уровня подъема (спада) должно быть больше (меньше) всех последующих.

Оба показателя S и d., асимптотически нормальны и имеют независимые распределения.

3. Проверятся с использованием t – критерия Стьюдента гипотеза о том, можно ли считать случайными разности S - µ и d =0

; , (23 )

где µ – среднее значение величины S, определенное для ряда, в котором уровни расположены случайным образом;

σ₁ – стандартная ошибка величины S;

σ₂ – стандартная ошибка величины d.

Значения µ, σ₁, σ₂ табулированы и приведены в соответствующих таблицах.

4. Далее необходимо сравнить расчетные значения t_s и t_d c табличными при заданном уровне значимости: если t_s < t_табл и t_d < t_табл , то гипотеза об отсутствии тренда в средней дисперсии подтверждается.

Рассмотрим в качестве примера определение наличия тренда в ряду динамики показателей демографической ситуации в Пензенской области [9].

Таблица 3. Показатель рождаемости в Пензенской области за 1990-1999гг.

Год	Yi Тыс. чел.	Ui	ei
1990 1991 1992 1993 1994 1995 1996 1997 1998 1999	19.4 17,6 15,6 13,8 13,5 12,8 12,0 11,5 11,6 11,2	0 0 0 0 0 0 0 0 1 0	0 1 1 1 1 1 1 1 0 1

По формуле (22) определяем S=9, d=-7. По таблицам [7] при n=10,  =3,858, ₁ = 1,288, ₂ = 1,964.

Подставляя полученные значения в формулу ( 23 ) получим

; .

Ближайшее табличное значение t_табл для двухстороннего критерия при уровне значимости 0,10 равно t_табл=1,812, т. е. t_табл t_S, t_табл  t_d. Следовательно гипотеза об отсутствии тенденции в рассматриваемом ряду отвергается и принимается наличие тенденции.