
- •Сбор, промысловая подготовка продукции скважин
- •Введение
- •1. Состав нефти и газа
- •1.1. Общие положения
- •1.2. Пересчет массового состава углеводородной смеси в объемный
- •1.3. Пересчет молярного (объемного) состава газовой смеси в массовый
- •Пример расчета
- •1.4. Пересчет массового состава жидкой углеводородной смеси в объемный
- •1.5. Пересчет объемного состава жидкой углеводородной смеси в массовый
- •1.6. Пересчет массового состава жидкой углеводородной смеси в молярный состав
- •2. Расчет физических свойств нефти и попутного газа
- •2.1. Расчет средней молекулярной массы смеси
- •2.2. Расчет средней плотности углеводородной (жидкой и газообразной) смеси
- •3. Расчет содержания тяжелых углеводородов в попутном нефтяном газе
- •3.1. Общие положения
- •3.2. Пример расчета содержания тяжелых углеводородов по данному массовому составу
- •3.3. Пример расчета содержания тяжелых углеводородов в попутном нефтяном газе по данному объемному составу.
- •4. Расчет процесса сепарации нефти от газа
- •5. Расчет производительности газонефтяных сепараторов
- •5.1. Общие теоретические положения
- •5.2. Механический расчет газонефтяных сепараторов
- •6. Расчет промысловых сборных трубопроводов
- •6.1. Общие положения
- •6.2. Расчет простого трубопровода для перекачки нефти
- •6.3. Гидравлический расчет промысловых сборных трубопроводов при движении нефтегазовых смесей
- •6.4. Расчет сложного сборного нефтепровода
- •7. Расчет распределения температуры нефти по длине сборного нефтепровода
- •7.1. Краткое описание метода расчета
- •8. Расчет потерь углеводородов от испарения нефти
- •8.1. Общие положения
- •8.2. Расчет потерь углеводородов при хранении нефти в резервуарах
- •8.2.1. Определение потерь углеводородов при загрузке резервуаров.
- •8.2.2. Определение потерь углеводородов при малых дыханиях резервуара
- •9. Расчет теплообменной аппаратуры
- •9.1. Виды теплообмена
- •9.2. Критерии подобия
- •9.3. Схемы перемещения взаимодействующих потоков.
- •9.4. Методика расчета теплообменников
- •110 °С безводная нефть 40 °с
- •10. Тепловые расчеты по нагреву нефтяных эмульсий
- •10.1. Определение количества тепла, необходимого на нагрев нефти и эмульсий
- •10.2. Тепловой расчет блочного деэмульсатора
- •11. Расчет отстойной аппаратуры
- •11.1. Общие теоретические положения
- •Список литературы
- •Содержание
11. Расчет отстойной аппаратуры
11.1. Общие теоретические положения
Технологический расчет отстойной аппаратуры заключается в определении пропускной способности отстойника или его размеров.
Если скорость слияния капель воды с водной подушкой - слоем воды в отстойнике - меньше скорости накопления частиц на водонефтяном разделе, то между нефтью и водной подушкой образуется переходной слой, толщина которого уменьшается к выходу от отстойника.
Обводненность нефти на выходе из отстойника определяют по содержанию мелких капель воды, время осаждения которых больше времени осевого перемещения разделяемой эмульсии в отстойнике. Скорость движения эмульсии вдоль отстойника от входа до выхода непрерывно уменьшается от значения на входе
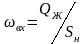 (11.1)
(11.1)
до значения на выходе
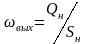 (11.2)
(11.2)
где Qж- количество жидкости (эмульсии), непрерывно поступающее в отстойник для разделения за единицу времени;
72
SH - площадь поперечного сечения, занятая слоем нефти (эмульсии) на входе в отстойник;
Qн - количество эмульсии с остаточным содержанием воды, непрерывно вытекающее из отстойника в единицу времени.
За время прохождения эмульсии от входа до выхода из отстойника концентрация дисперсной фазы в эмульсии изменяется. В верхней части отстойника она уменьшается по сравнению с первоначальной концентрацией. Следовательно, вязкость эмульсии по высоте в отстойнике переменна, причем в верхней части отстойника она уменьшается вдоль горизонтальной оси от входа до выхода. По вертикали в каждом сечении отстойника вязкость эмульсии возрастает, от минимальной у верхней образующей отстойника до максимальной на границе с водной подушкой. Такой сложный характер изменения вязкости эмульсии в отстойнике определяется кинетикой гравитационного разделения фаз. Следовательно, горизонтальная составляющая скорости эмульсии в отстойнике максимальна в верхнем и минимальна в нижнем слоях эмульсии.
Принимая время осаждения максимальных капель воды, выносящихся потоком нефти, равным времени движения эмульсии вдоль зоны отстоя, получаем возможность рассчитать пропускную способность отстойника
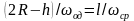 ,
(11.3)
,
(11.3)
где R - радиус отстойника; h - высота слоя воды в отстойнике; ωод i - скорость осаждения капель воды диаметром di в эмульсии, из которой выносятся потоком нефти все отставшие капли меньшего размера; l- часть длины отстойника от сечения, где начинается гравитационное разделение эмульсии (ввод), до сечения, где оно прекращается (выход).
Из (11.3) следует
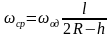 (11.4)
(11.4)
Пропускная
способность отстойника из (11.1) определяется
как
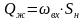 .
Так как средняя скорость движения
эмульсии в отстойнике может быть принята
как средняя арифметическая на входе и
выходе, то
.
Так как средняя скорость движения
эмульсии в отстойнике может быть принята
как средняя арифметическая на входе и
выходе, то
73
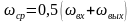 ,
,
откуда
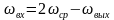 ,
,
или с учетом (11.2)
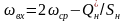 .
.
Таким образом, пропускная способность отстойника будет
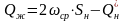 .
(11.5)
.
(11.5)
Из материального баланса работы отстойника, пренебрегая захватом нефти дренажной водой, можно показать, что
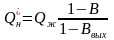 .
(11.6)
.
(11.6)
Следовательно, из (11.5) с учетом (11.6) после преобразований имеем
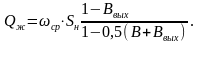 (11.7)
(11.7)
Подставляя (11.4) в (11.7), получим
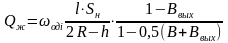 (11.8)
(11.8)
Так как скорость стесненного осаждения капель равна
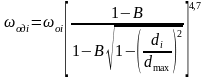
а свободного при Re<2- соответственно
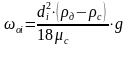 ,
,
то пропускная способность отстойника будет
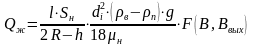 ,
(11.9)
,
(11.9)
74
где
F(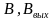 )
- функция обводненности на входе и выходе
из отстойника
)
- функция обводненности на входе и выходе
из отстойника
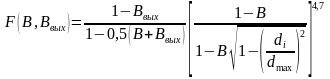
(11.10)
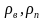 —
плотность
воды и нефти в отстойнике соответственно,
кг/м; l
- длина зоны отстоя, м;
—
плотность
воды и нефти в отстойнике соответственно,
кг/м; l
- длина зоны отстоя, м;
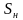 -
площадь поперечного сечения отстойника,
занятая эмульсией на входе в зону отстоя,
м; R
-
радиус отстойника, м; h
-максимальная
высота водной подушки в отстойнике в
зоне отстоя, м;
-
площадь поперечного сечения отстойника,
занятая эмульсией на входе в зону отстоя,
м; R
-
радиус отстойника, м; h
-максимальная
высота водной подушки в отстойнике в
зоне отстоя, м;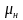 —
вязкость
нефти в отстойнике, Па
—
вязкость
нефти в отстойнике, Па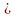 с;
d
— максимальный
диаметр капель воды, которые вместе с
каплями меньшего размера могут выноситься
из отстойника потоком нефти, м,
В, Ввых
-
обводненность
эмульсии на входе в зону отстоя и выходе
из нее;
с;
d
— максимальный
диаметр капель воды, которые вместе с
каплями меньшего размера могут выноситься
из отстойника потоком нефти, м,
В, Ввых
-
обводненность
эмульсии на входе в зону отстоя и выходе
из нее;
 - максимальный размер капель воды в
эмульсии на входе в зону отстоя, м.
- максимальный размер капель воды в
эмульсии на входе в зону отстоя, м.
Используя решение [7, формула (6.45)]
 ,
,
Следует, что
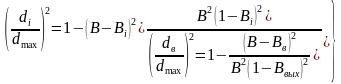
(11.11)
где dв - максимальный диаметр капель, выносимый из отстойника с потоком нефти.
Связь между di и максимальным диаметром капли, выносимым из отстойника, можно установить следующим образом.
75
Перед
выходом нефти из отстойника в зоне
отстоя в дренаж уходит последняя капля
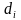 ,
которая
являлась для остающихся капель
максимальной, поэтому обводненность
слоя эмульсии с каплями
,
которая
являлась для остающихся капель
максимальной, поэтому обводненность
слоя эмульсии с каплями
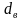 может
быть, по аналогии с (11.11), представлена
в виде
может
быть, по аналогии с (11.11), представлена
в виде
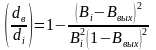 .
(11.12)
.
(11.12)
Таким
образом, система уравнений (11.11) и (11.12)
содержит три неизвестных
,
, ,
,
следовательно, может быть решена. Представим (11.9) в виде
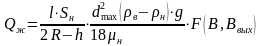 ,
(11.13)
,
(11.13)
где
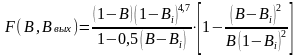 .
(11.14)
.
(11.14)
Необходимо отметить, что доля воды в потоке нефти на выходе из отстойника является функцией высоты водяной подушки, пропускной способности отстойника и его конструктивных параметров. Как правило, в дренажной воде содержится примесь нефти, количество которой также является функцией, перечисленных выше параметров. Поэтому расчет пропускной способности отстойника по (11.14) достаточно приближенный.
Задача 33. Исследовать влияние высоты слоя водяной подушки на пропускную способность булита-отстойника.
Решение. Пусть высота слоя водяной подушки равна h (рис. 9). В соответствии с (11.13) для расчета пропускной способности отстойника необходимо знать часть площади поперечного сечения отстойника , занятую нефтью (эмульсией).
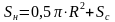 (11.15)
где R
- радиус
булита-отстойника; Sc
- часть
площади сечения булита-отстойника между
параллельными максимальным сечением
(диаметром) и зеркалом воды.
(11.15)
где R
- радиус
булита-отстойника; Sc
- часть
площади сечения булита-отстойника между
параллельными максимальным сечением
(диаметром) и зеркалом воды.
76

Слагаемое Sc может быть найдено следующим образом. Элемент площади круга
dSc=2y·dx
= 2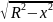 ·dx.
·dx.
Следовательно,
Sc
=
2
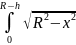 ·dx
.
·dx
.
Для вычисления интеграла положим u = ; dv = dx. Тогда
du = - (x·dx) / ( ), v = x.
Следовательно, после некоторых преобразований
2
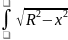 ·dx
= x
+ R2·arcsin(x/R)
+ C,
·dx
= x
+ R2·arcsin(x/R)
+ C,
т.е.
Sc
= 2
·dx
= x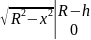 + R2·arcsin(x/R)
+ R2·arcsin(x/R)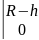 =
=
=
(R- h)
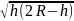 + R2
·arcsin
(R-h) / R. (11.16)
+ R2
·arcsin
(R-h) / R. (11.16)
Пропускная способность булита-отстойника определяется уравнением (11.13), в котором множитель, зависящий от высоты слоя водяной подушки, равен отношению SH/(2R - h). Поэтому нужно исследовать на экстремум именно этот множитель. Так как
SH = ½ πR2 + (R-h) + R2·arcsin (R-h) / R (11.17)
то
SH
/
(2R-h)
= R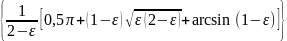 ,
(11.18)
,
(11.18)
77
где ε = h/R - относительная высота водяной подушки в буллите-отстойнике.
Обозначим
F(ε)
= 1
/ (2 – е)·[0,5π
+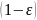
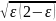 + arcsin·(l
- ε)].
(11.19)
+ arcsin·(l
- ε)].
(11.19)
Найдем производную от F(ε) по ε, которая после преобразований будет равна
F´(ε)
= 1
/ (2 – е)2[0,5π
+
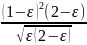 + arcsin·(l
- ε)
-
+ arcsin·(l
- ε)
-
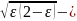
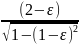 ].
(11.20)
].
(11.20)
Производная F'(ε) равна нулю, если
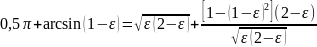
или
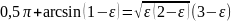 (11.21)
(11.21)
Значение ε, удовлетворяющее уравнению (11.21) (табл. 36), может быть найдено графически, построением графиков зависимостей левой и правой частей равенства от относительной высоты водяной подушки (рис. 10).
Из рис. 10 следует, что функция F(ε) имеет экстремум при ε = 0,46.
Таблица 36
ε |
1-ε |
arcsin(l-ε) |
Значения |
|
левой части уравнения |
правой части уравнения |
|||
0,1 |
0,9 |
1,12 |
2,69 |
1,26 |
0,2 |
0,8 |
0,93 |
2,50 |
1,68 |
0,3 |
0,7 |
0,78 |
2,35 |
1.93 |
0,4 |
0,6 |
0,64 |
2,21 |
2,08 |
0,5 |
0,5 |
0,52- |
2,09 |
2,17 |
0,6 |
0,4 |
0,41 |
1,98 |
2,20 |
0,7 |
0,3 |
0,30 |
1,87 |
2,19 |
0,8 |
0,2 |
0,20 |
1,77 |
2,16 |
0,9 |
0,1 |
0,10 |
1,67 |
2,09 |
78
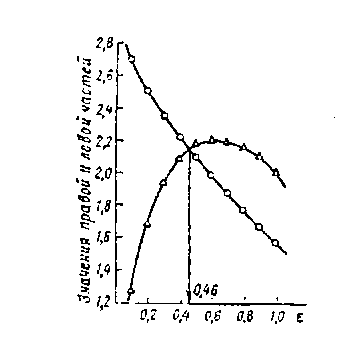
Рис. 10. Графики для решения уравнения (11.21)
Задача 34. Рассчитать диаметр и длину отстойной секции гравитационного булита-отстойника, обеспечивающего заданную пропускную способность и степень разделения эмульсии на нефть и воду.
Решение. Эффективное разделение фаз в гравитационном отстойнике происходит при условии соблюдения в зоне отстоя ламинарного режима течения эмульсии, т.е. при Rе 2300. Следовательно,
vжDэρж /μж ≤ 2300, (11.22)
где vж - скорость горизонтального движения эмульсии в зоне отстоя в отстойнике, м/с; Dэ - эквивалентный гидравлический диаметр поперечного сечения потока эмульсин в отстойнике на входе в зону отстоя, м; ρж и μж - плотность и вязкость эмульсии на входе в зону отстоя, кг/м и Па·с, соответственно. Так как
Sн = 0,25πD2 (11.23)
а скорость потока эмульсин на входе в зону отстоя
vж = Qж / Sн = 4Qж / πDэ2 (11.24)
то, подставив (11.24) в (11.22), получим
Dэ (4/2300π)·(Qжρж/μж). (11.25)
Из (11.23) с учетом (11.16) и (11.18) следует
Dэ = D{1/π[0,5π + (1 - ε) · + arcsin(l - ε)]}0,5 . (11.26)
Поэтому диаметр булита-отстойника с водяной подушкой на заданную пропускную способность может быть рассчитан по формуле
79
D
≥ 0,981·10-3·(Qжρж/μж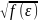 ),
(11.27)
),
(11.27)
где Qж - нагрузка на отстойник по жидкости в зоне отстоя, м3/с; ρж - плотность эмульсии на входе в зону отстоя, кг/м3; μж - вязкость эмульсии на входе в зону отстоя, Па·с; f(ε) - функция относительной высоты водяной подушки в зоне отстоя
f(ε) = 0,5π + (1-ε) + arcsin(l - ε). (11.28)
При ε = 0,46 пропускная способность гравитационного отстойника максимальна, поэтому, подставив ε = 0,46 в (11.28), находят
f(0,46)
= 0,5π + (1 - 0,46)·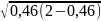 + arcsin(l
- 0,46) = 2,596.
+ arcsin(l
- 0,46) = 2,596.
Учитывая, что f(0,46) = 2,596 и подставляя в (11.27), получают
D
≥ 0,6·10-3·(Qжρж/μж (11.29)
(11.29)
Из (11.29) следует, что пропускная способность гравитационного отстойника заданного диаметра высотой водяной подушки 0,23D может быть рассчитана по той же формуле, т.е.
Qж 1645·D·μж / ρж. (11.30)
Необходимую длину отстойника определяют из условия, равенства времени осаждения капель воды от верхней образующей до водонефтяного раздела и временем их пребывания в зоне отстоя
(D – h) / ωодi = l/vж (11.31)
где ωодi - скорость стесненного осаждения капли воды диаметром di в полидисперсной эмульсии в зоне отстоя, м/с; l - эффективная длина зоны гравитационного разделения отстойника, т.е. длина зоны отстоя, не возмущаемая условиями ввода и вывода эмульсии, м; vж - горизонтальная скорость движения эмульсии в зоне отстоя, м/с. Так как
ωодi = ωоi(1 – Bi)4,7, (11.32)
то из (11.31) после преобразований следует
1
=
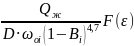 (11.33)
(11.33)
где F(ε) — функция относительной высоты водяной подушки в зоне отстоя
F(ε)
=
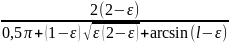 .
(11.34)
.
(11.34)
80
Общая длина отстойника будет определяться как сумма
L = l + lk (11.35)
где L — общая длина отстойника, м; l - длина зоны гравитационного отстоя, м; lk - конструктивная длина секций ввода и вывода эмульсии в отстойнике, м.
Подставив в (11.33) диаметр отстойника из (11.27), получают
1
=
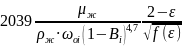 .
(11.36)
.
(11.36)
При ε = 0,46 из (11.36) с учетом (11.28) следует
1 =
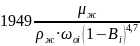 (11.37)
(11.37)
Задача 35. Диаметр отстойника 3,4 м, плотность нефти 860 кг/м3, воды 1100 кг/м3, обводненность эмульсии на входе 30%, вязкость нефти 5 мПа·с. Оценить пропускную способность отстойника по жидкости по (11.30).
Решение. Плотность эмульсии рассчитывают по правилу аддитивности
ρж = ρH(1-В) + ρB·В = 860(1-0,3)+1100·0,3 = 932 кг/м3.
Вязкость эмульсии оценивают по формуле [7]
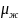 =
=
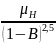 = 5 / (1-0,3)2,5
= 12мПа·с.
= 5 / (1-0,3)2,5
= 12мПа·с.
Тогда пропускная способность булита-отстойника типа УПС-6300/6М, обеспечивающего ламинарный режим движения, при принятых параметрах
будет
Qж = 1645·(3,4·12·10-3 / 932)·86400 = 6222 м3/сут.
Задача 36. Определить необходимый диаметр горизонтального отстойника для предварительного сброса воды с относительной высотой водяной подушки в нем ε = 0,46, если максимальная нагрузка на него по жидкости не превысит 6300 т/сут., а обводненность эмульсии в зоне отстоя колеблется от 30 до 45 %. Вязкость нефти в условиях эксплуатации отстойника из-за температурных колебаний может изменяться от 3,5 до 4 мПа·с.
81
Решение. Как следует из формулы (11.29), справедливой для ε = 0,46, диаметр отстойника, в котором будет обеспечен ламинарный режим движения эмульсии в зоне отстоя, прямо пропорционален нагрузке на него и обратно пропорционален вязкости эмульсии.
Допускают, что вязкость эмульсии может быть оценена по формуле [7]
=
где
В
—
обводненность эмульсии;
и
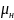 - вязкость эмульсии и нефти соответственно;
тогда
- вязкость эмульсии и нефти соответственно;
тогда
D
0,6·10-3·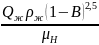
При прочих равных условиях максимальный диаметр отстойника получается при минимальном значении обводненности эмульсии.
Поэтому
принимают в расчетах B
= 0,3, вязкость нефти
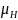 =
3,5 мПа·с и получают, что
=
3,5 мПа·с и получают, что
D
≥ 0,6·10-3· =5,1
м
=5,1
м
При прочих равных условиях диаметр отстойника минимален при максимальной обводненности эмульсии, поэтому принимают в расчетах В = 0,45, вязкость нефти = 4 мПа·с и получают, что
D
≥ 0,6·10-3·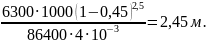
Отстойники диаметром более 3,4 м промышленностью не выпускаются, следовательно, выбирают отстойник диаметром 3,4 м. Но выбранный отстойник не может обеспечить необходимую нагрузку на него в 6300 т/сут. при ламинарном режиме течения эмульсии в нем и при других значениях входных параметров. Поэтому оценивают допустимую нагрузку на него при обводненности В = 0,3 и вязкости нефти = 3,5 мПа·с по формуле (11.30)
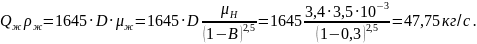
или
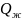 =
47,75·(86400/1000)
=
4126 т/сут.
=
47,75·(86400/1000)
=
4126 т/сут.
82
Таким образом, при нагрузке 6300 т/сут. необходимо установить не менее двух отстойников диаметром 3,4 м.
Допустимую нагрузку на отстойник в наиболее тяжелых условиях, если диаметр отстойника 2 м, оценивают по формуле (11.30)
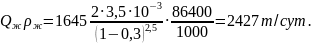
Нагрузку 6300 т/сут. можно пропустить только через три отстойника диаметром 2 м.
Наиболее выгодный вариант может определить технико-экономический анализ.
Задача 37. В продукцию скважин на групповом сборном пункте вводят ПАВ-деэмульгатор и насосом откачки его подают на дожимную насосную станцию, оборудованную двумя буферными емкостями диаметром 2 м и объемом 115 m3/с отводами для предварительного сброса вода. Нагрузка на каждую буферную емкость колеблется от 2000 м3/сут. с обводненностью 37,7% до 1500 м3/сут. с обводненностью 36,6%. Высоту водяной подушки в емкостях поддерживают на постоянном уровне 60 см.
Оценить содержание воды в нефти на выходе из буферных емкостей, если вязкость нефти 5 мПа·с, плотность нефти 860 кг/м3, а воды — соответственно 1050 кг/м3.
Решение. Зная объем буферной емкости, находят ее длину
L = 4V / (π·D2) = (4·115) / (4π) = 36,6 м.
Так как длина зоны отстоя меньше длины емкости на суммарную длину секций ввода и вывода эмульсии, принимают длину зоны отстоя l = 30 м. Время задержки эмульсии в емкости
tзад = l·SH / Qж
где SН — площадь поперечного сечения в емкости, занятая нефтью, м2;
Qж - нагрузка на емкость по жидкости, м3/с.
Так как высота слоя воды в емкости h = 0,6 м, то ε = 0,6, следовательно,
SH
=
R2
[0,5π
+
(1 – 0,6)
·
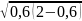 + arcsin(l – 0,6)]
= 2,349·R2.
+ arcsin(l – 0,6)]
= 2,349·R2.
83
Зная нагрузку на первую емкость по жидкости 2000 м3/сут., находят время
задержки эмульсии в ней
tзад = ((30·12·2,349) / 2000)·86400 = 3044 с.
Очевидно, что время оседания капель воды в буферной емкости toe равно времени задержки эмульсии tзад в ней, т.е. tос = tзад. С другой стороны, время оседания капель воды в эмульсии в емкости равно
toc = (D - h)/wod i,
где wod i - скорость стесненного оседания капли эмульсии размером di м/с.
Откуда можно найти скорость wod i:
wod i = D - h/toc = 2 - 0,6/3044 = 0,44·10-3 м/с.
Используя решение [7, формула (6.45)], можно выразить di через dmax
di2
=
dmax2(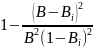 )
)
Как следует из условий задачи, в продукцию скважины на групповом сборном пункте подают ПАВ и затем ее перекачивают насосом откачки до дожимной насосной станции. Промысловый трубопровод от группового сборного пункта до ДНС можно рассматривать как своеобразный каплеобразователь-укрупнитель и, принять поэтому, максимальный размер капель в эмульсии на входе в буферную емкость в диапазоне dmax = 300...350 мкм. Таким образом, можно записать следующее равенство:
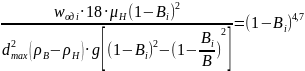 (11.38)
(11.38)
в котором содержится только одно неизвестное - остаточная обводненность нефти после осаждения капель размером больше di. Подставим числовое значение известных величин, входящих в это равенство, при dmax =325 мкм
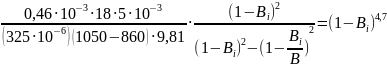 (11.39)
(11.39)
Полученное равенство можно решить графически (рис. 11).
84
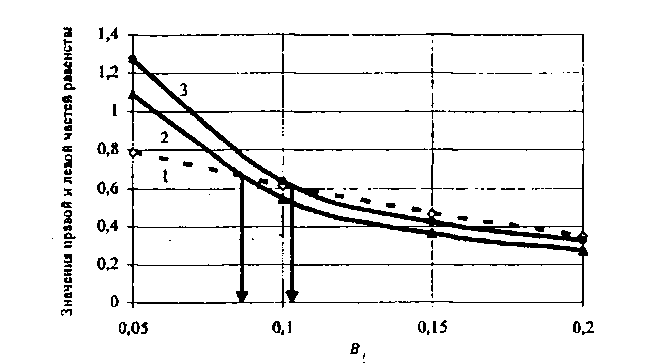
Рис. 11. Графики для решения уравнения (11.39)
1 - значения правой часта равенства;
2 и 3 - значения левой часта при dm = 325 и 350 мкм соответственно
В табл.
37 представлены результаты нахождения
значений левой и правой части равенства
в зависимости от
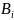 .
.
Таблица 37
Вi |
Значение правой части уравнения (11.39) |
Значение левой части уравнения (11.39) при |
|
dmax =325 мкм |
dmax =250 мкм |
||
0,05 |
0,786 |
1,2639 |
1,090 |
0,10 |
0,609 |
0.631 |
0,544 |
0,15 |
0,466 |
0.422 |
0.364 |
0,20 |
0,350 |
0,321 |
0,276 |
Из графика следует, что в зависимости от величины dmax в эмульсии, входящей в отстойник, на выходе из отстойника получают нефть с различным содержанием воды: при dmax= 325 мкм обводненность нефти на выходе из отстойника меньше 12,5%, а при dmax = 350 мкм выходная обводненность продукции меньше 8 %.
Результаты аналогичных расчетов при нагрузке на буферные емкости по 1500 м3/сут., и содержании воды в эмульсии 36,6 % представлены ниже.
85
tзад = (30·12·2,349) / 1500·86400 = 4059 с.
Таблица 38
Результаты решения уравнения (11.41)
Отношение δ |
Значения функции А(δ) при значениях В (рис. 12) |
|||||||
0,05 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
|
0,1 |
0,1776 |
0,1655 |
0,1424 |
0,1206 |
0,1000 |
0,0805 |
0,0623 |
0,0451 |
0,2 |
0,3310 |
0,3034 |
0,2522 |
0,2061 |
0,1648 |
0,1279 |
0,0952 |
0,0663 |
0,3 |
0,4610 |
0,4153 |
0,3330 |
0,2621 |
0,2014 |
0,1499 |
0,1067 |
0,0710 |
0,4 |
0,5685 |
0,5030 |
0,3883 |
0,2934 |
0,2158 |
0,1533 |
0,1037 |
0,0652 |
0,5 |
0,6543 |
0,5681 |
0,4214 |
0,3047 |
0,2135 |
0,1437 |
|
|
0,6 |
0,7192 |
0,6123 |
0,4351 |
0,2999 |
|
|
|
|
0,7 |
0,7641 |
0,6370 |
0,4343 |
|
|
|
|
|
0,8 |
0,7896 |
0,6438 |
|
|
|
|
|
|
0,9 |
0,7966 |
0,6342 |
|
|
|
|
|
|
Скорость стесненного осаждения капли эмульсии диаметром d составит
wod i = (2-0,6)/4059 = 0,345·10-3 м/с.
При dmax =325 мкм из формулы (11.38) получим
0,1577=(l-δ·B)2,7[(l-δ·B)2-(l-δ)2],
где δ - отношение обводненности нефти на выходе из отстойника к ее обводненности на входе δ =В i /В.
Обозначим
A(δ) =(l-δ·B)2,7[(l-δ·B)2-(l-δ)2]. (11.40)
В общем случае 0 δ 1, соответственно 0 < В < 0,8 (табл. 38). Используя номограмму решения уравнения (11.40) и значение
A(δ) = 0,1577 при В = 36,6%, из рис. 12 найдем, что δ = 0,17, поэтому Вi = 0,17·36,6 = 6%.
86
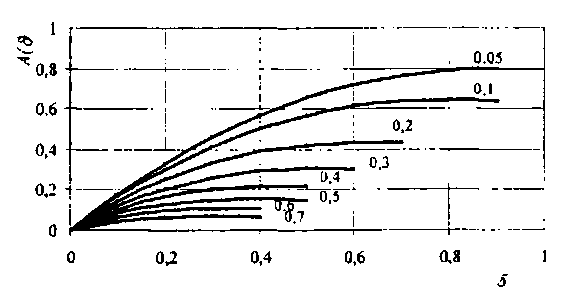
Рис. 12. Номограмма значений правой части уравнения (11.40) при
различных отношениях обводненности на входе 3. На кривых указаны об-
водненности эмульсии на выходе В
Таким образом, для оценки содержания воды в эмульсии на выходе из отстойника необходимо знать максимальный диаметр капель в эмульсии на входе в зону гравитационного отстоя.
